Bạn đang tìm kiếm một công thức? Tính diện tích hình vuông để giải toán. Hình vuông là gì? Tính chất và tín hiệu nhận mặt hình vuông? Công thức tính diện tích hình vuông? Công thức tính chu vi hình vuông? Setup các bài toán hình vuông thường gặp? Mọi thông tin cần biết về ô vuông sẽ được TTmobile trả lời ngay dưới đây, hãy chú ý theo dõi.
Hình vuông là gì?
Hình vuông là tứ giác có 4 cạnh bằng nhau, 4 góc vuông, các cặp cạnh đối song song và bằng nhau.
Bạn đang xem bài: 4 công thức tính diện tích hình vuông, chu vi, tính chất từ A – Z
Hình vuông có thể được coi là hình chữ nhật có các cạnh bằng nhau hoặc hình thoi có hai đường chéo bằng nhau.
5 Tính chất của hình vuông cần biết
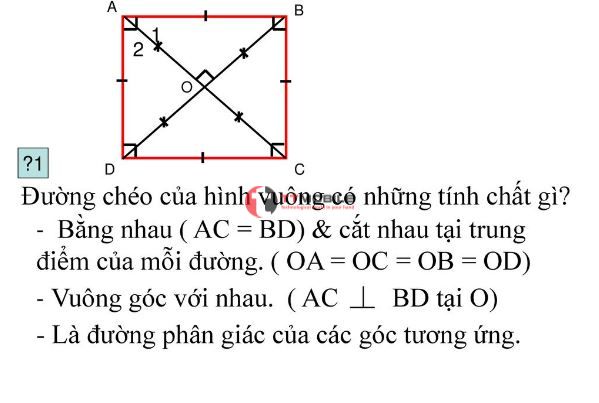
– Một hình vuông có hai đường chéo bằng nhau và vuông góc với nhau, cắt nhau tại trung điểm của mỗi đoạn thẳng.
– Hình vuông có một đường chéo sẽ chia hình vuông đó thành hai phần bằng nhau.
– Hình vuông có tâm của đường tròn nội tiếp và đường tròn ngoại tiếp trùng với giao điểm của hai đường chéo của hình vuông.
– Là hình vuông nhưng giao điểm của đường trung tuyến, đường trung trực và đường phân giác trùng nhau tại một điểm.
– Hình vuông có các tính chất của hình thoi, hình bình hành, hình chữ nhật.
5 Tín hiệu nhận mặt ô vuông
– Hai đường chéo của hình chữ nhật vuông góc với nhau là hình vuông.
Hình vuông là hình chữ nhật có hai cạnh kề nhau bằng nhau.
– Hình chữ nhật có đường chéo là tia phân giác của một góc là hình vuông.
Hình vuông là hình thoi có hai đường chéo bằng nhau.
Hình vuông là hình thoi có một góc vuông.
=> Do đó, một tứ giác vừa là hình chữ nhật vừa là hình thoi thì tứ giác đó là hình vuông.
Công thức tính chu vi hình vuông
Chu vi hình vuông được tính bằng cách nhân 4 cạnh hay nói cách khác chu vi hình vuông bằng tổng độ dài của 4 cạnh cộng lại với nhau.
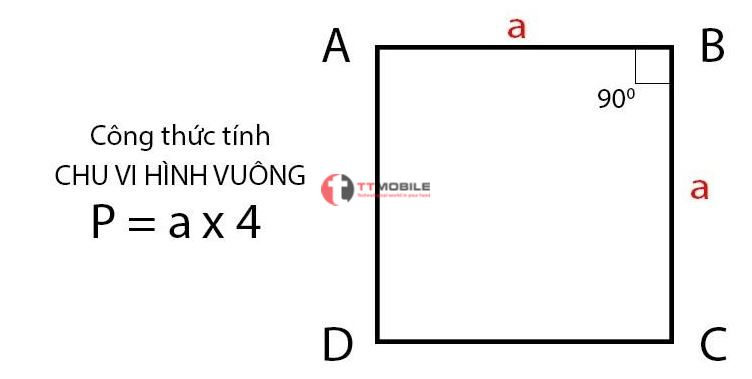
Công thức tính chu vi hình vuông như sau:
P = ax 4
Trong đó:
– P là chu vi hình vuông
– a là độ dài một cạnh của hình vuông
Ví dụ: Tính chu vi hình vuông ABCD có độ dài cạnh 4 cm
Dung dịch:
Chu vi hình vuông ABCD là: 4 x 4 = 16 cm.
Xem thêm:
- Tính chất của hình thang vuông, công thức tính diện tích chu vi với các ví dụ
- 9 công thức diện tích tam giác đáng chú ý
- 3 Công thức tính diện tích hình thang
- Công thức tính diện tích và thể tích của hình nón với 4 ví dụ hay
- Tổng hợp 5 công thức tính diện tích tam giác đều, vuông, cân
Công thức tính diện tích hình vuông
Diện tích hình vuông là phần hình vuông có thể nhìn thấy bởi mặt phẳng.
Diện tích của hình vuông sẽ bằng cạnh nhân với cạnh.
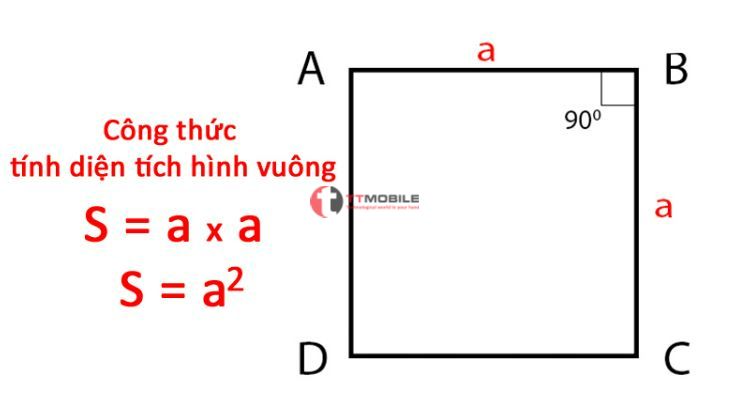
Cụ thể, công thức tính diện tích Hình vuông như sau:
S = axa
Trong đó:
– S là diện tích hình vuông
– a là cạnh của hình vuông đó.
Ví dụ:
Cho hình vuông ABCD có độ dài cạnh là 5 cm. Tính diện tích hình vuông đã cho.
Dung dịch:
Diện tích hình vuông ABCD là: 5 x 5 = 25 cm2
Trả lời: Diện tích hình vuông ABCD là 25 cm2
Một số công thức tính diện tích Hình vuông khác:
Công thức tính diện tích hình vuông bằng tổng diện tích 2 tam giác vuông cân.
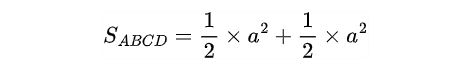
Công thức tính diện tích hình vuông bằng tổng diện tích 2 hình chữ nhật.
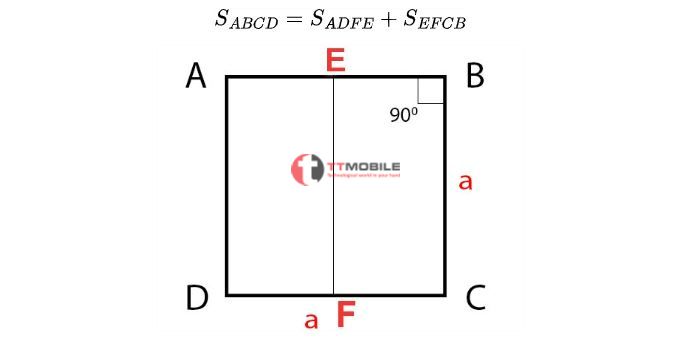
Một số xem xét lúc giải toán Hình vuông
– Các cạnh của hình vuông phải cùng một đơn vị đo. Xin xem xét rằng lúc tính diện tích hình vuôngchu vi của một hình vuông hay bất kỳ hình nào, cần xem xét rằng các cạnh của hình đó phải cùng một đơn vị đo, nếu là cm thì tất cả là cm, hoặc nếu là m thì tất cả đều phải dùng m.
Nếu bài toán cho các đơn vị đo của hình vuông không giống nhau thì cần quy đổi về cùng một đơn vị đo rồi thực hiện công thức tính diện tích hình vuông.
– Đơn vị tính diện tích hình vuông là đơn vị đo diện tích như cm2 ta ko được dùng các đơn vị khác lúc tính diện tích hình vuông. Bạn cần chú ý điều này vì nhiều người quên mất đơn vị diện tích.
– Đơn vị đo chu vi hình vuông là đơn vị đo độ dài khác với đơn vị đo diện tích. Đơn vị đo chu vi hình vuông vẫn được dùng làm đơn vị chung như m, cm, v.v.
– Lúc nào Tính diện tích hình vuôngtính chu vi của hình vuông là điều cần thiết để nắm được công thức tính vì công thức tính diện tích hoặc chu vi của các hình thường bị nhầm lẫn với nhau dẫn tới kết quả sai.
Bài tập về hình vuông
Bài tập 1
Nếu kéo dài một mảnh đất hình vuông ra một cạnh 5cm thì chu vi hình chữ nhật là 110m. Sau lúc mở rộng diện tích, hãy tính mảnh đất có diện tích.
Câu trả lời:
Chu vi mảnh đất hình vuông là: 110 – 5 x 2 = 100 cm
Cạnh của hình vuông (cũng là chiều rộng của hình chữ nhật) là: 100: 4 = 25 cm
Chiều dài của hình chữ nhật là: 25 +5 = 30 cm
=> Sau lúc mở rộng diện tích khu đất sẽ là 25 x 30 = 750 cm2
Bài tập 2
Cho ABC là tam giác vuông tại A, phân giác AD. Gọi M, N là chân đường vuông góc kẻ từ D lên AB, AC. Chứng minh rằng tứ giác AMDN là hình vuông.
Câu trả lời:
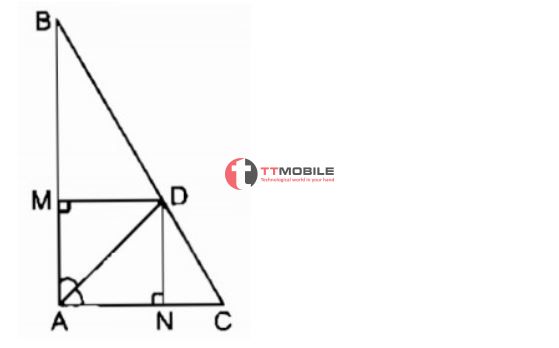
Xét tứ giác AMDN, ta có:
(MAN) = 90o (gt)
DM ⊥ AB (gt)
(AMD) = 90o
DN AC (gt) (AND) = 90o
Do đó, tứ giác AMDN là hình chữ nhật (vì có ba góc vuông),
Mặt khác, hình chữ nhật AMDN này có đường chéo AD là tia phân giác của A
=> Vậy hình chữ nhật AMDN là hình vuông.
Bài tập 3
Cho hình vuông ABCD. Trên AB, BC, CD, DA tuần tự lấy các điểm E, K, P, Q sao cho AE = BK = CP = DQ. Tứ giác EKPQ là hình gì? Vì sao?
Câu trả lời:
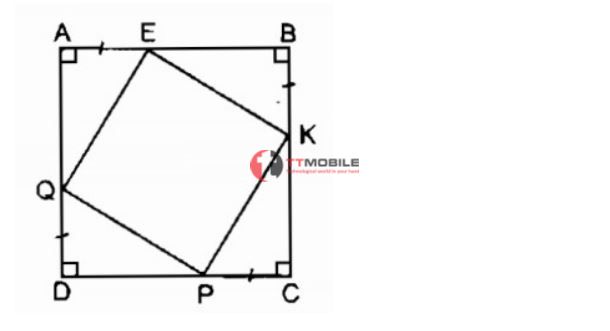
Chúng ta có:
AB = BC = CD = DA (gt)
AE = BK = CP = DQ (gt)
Suy ra: EB = KC = PD = QA
* Xét ΔAEQ và ΔBKE, ta có:
AE = BK (gt) A = B = 90o
QA = EB (đã chứng minh ở trên)
Suy ra: AEQ = BKE (cgc) ⇒ EQ = EK (1)
* Xét ΔBKE và ΔCPK, ta có:
BK = CP (gt) B = C = 90o
EB = KC (đã chứng minh ở trên)
Suy ra: BKE = CPK (cgc) ⇒ EK = KP (2)
* Xét ΔCPK và ΔDQP, ta có:
CP = DQ (gt)
C = D = 90o
DP = CK (đã chứng minh ở trên)
Suy ra: CPK = DQP (cgc) KP = PQ (3)
Từ (1), (2) và (3), nó như sau:
EK = KP = PQ = EQ Hay tứ giác EKPQ là hình thoi.
Trái lại: AEQ = BKE
(AQE) = (BKE)
Nhưng (AQE) + (AEQ) = 90o
(BEK) + (AEQ) = 90o
⇒ (BEk) + (QEK) + (AEQ) = 180o
Suy ra: (QEK) = 180o – (∠ (BEK) + (AEQ)) = 180o – 90o = 90o
Vậy tứ giác EKPQ là hình vuông.
Bài tập 4
Cho ABC là tam giác cân tại A. Trên cạnh BC lấy các điểm H, G sao cho BH = BG = GC. Qua H, G kẻ các đường vuông góc với BC cắt AB, AC tuần tự tại E và F. Tứ giác EFGH là hình gì? Vì sao?
Câu trả lời:
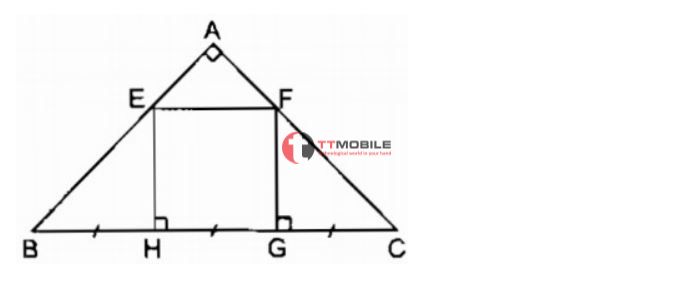
Vì ABC vuông góc tại A nên ∠B = C = 45o
Vì BHE vuông tại H có ∠B = 45o nên ΔBHE vuông góc tại H.
Vậy HB = HE
Vì CGF là hình vuông tại G nên có
∠C = 45o, do đó CGF là góc vuông tại G
Vì vậy GC = GF
Ta có: BH = BG = GC (gt)
Suy ra: HE = HG = GF
Vì EH // GF (hai đường thẳng đó cũng vuông góc với đường hãm thứ ba) nên tứ giác HEFG là hình bình hành (vì có một cặp cạnh đối diện bằng nhau).
Một lần nữa (EHG) = 90o
nên HEFG là hình chữ nhật.
Nhưng EH = HG (đã chứng minh ở trên).
Vậy HEFG là hình vuông.
Phần kết
TTmobile vừa tổng hợp cho bạn công thức Tính diện tích hình vuông, chu vi hình vuông, tính chất và tín hiệu nhận mặt hình vuông. Với những ví dụ khá cụ thể hi vọng sẽ giúp các bạn có thêm kiến thức giải toán cực nhanh và logic. Xin chân tình cảm ơn sự quan tâm và đón đọc của các bạn.
Bạn thấy bài viết 4 công thức tính diện tích hình vuông, chu vi, tính chất từ A – Z có khắc phục đươc vấn đề bạn tìm hiểu ko?, nếu ko hãy comment góp ý thêm về 4 công thức tính diện tích hình vuông, chu vi, tính chất từ A – Z bên dưới để tmdl.edu.vn có thể thay đổi & cải thiện nội dung tốt hơn cho độc giả nhé! Cám ơn bạn đã ghé thăm Website Trường Trung Cấp Nghề Thương Mại Du Lịch Thanh Hoá
Phân mục: Hỏi đáp
Nguồn: tmdl.edu.vn
Trang chủ: tmdl.edu.vn
Danh mục bài: Tổng hợp


