Hình tam giác được chia thành nhiều dạng, bạn muốn biết cách tính diện tích hình tam giác thường, hình vuông, hình cân, hình chóp tam giác đều hay tam giác đặc biệt? Nhìn chung, công thức tính diện tích tam giác là một kiến thức quan trọng và thường gặp trong quá trình ngồi trên ghế nhà trường. Dưới đây, TTmobile sẽ tổng hợp cho các bạn 9 công thức tính diện tích tam giác cần nhớ, xem ngay nhé.
Định nghĩa của một tam giác là gì?
– Hình tam giác là hình có ba đoạn thẳng nối các đỉnh và tổng ba góc trong một tam giác là 180 độ.
Bạn đang xem bài: 9 Công Thức Tính Diện Tích Tam Giác đáng chú ý
– Tam giác là đa giác có số cạnh ít nhất (3 cạnh) hoặc tam giác là đa giác đơn giản hay còn gọi là đa giác lồi (Đa giác lồi là đa giác có các góc luôn nhỏ hơn 180 độ).
Các dạng tam giác thường gặp có thể kể đến như: tam giác đều, tam giác đều, tam giác vuông, tam giác cân, tam giác vuông cân.
Diện tích hình tam giác là tất cả các phần mặt phẳng bên trong hình tam giác.
TAM GIÁC GỐC
Định nghĩa
Một tam giác bình thường là một tam giác có độ dài các cạnh và số đo góc trong khác nhau.
Công thức tính chu vi hình tam giác thường
Một tam giác bình thường có chu vi bằng tổng độ dài của ba cạnh.
P = a + b + c
Trong đó:
P là chu vi của tam giác
a, b, c lần lượt là 3 cạnh của tam giác.
Công thức về diện tích của một tam giác thường
Diện tích tam giác đều khi biết độ dài của chiều cao, nó sẽ được tính bằng ½ tích của chiều cao hạ xuống từ đỉnh nhân với độ dài của cạnh đáy đối diện với đỉnh của tam giác đó.
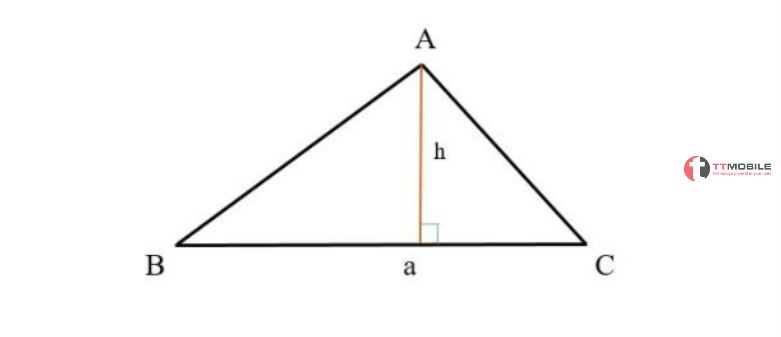
Công thức tính diện tích tam giác thường theo chiều cao:
S = xaxh
Trong đó:
a là độ dài cạnh đáy của tam giác.
h là Chiều cao nối từ đỉnh và vuông góc với đáy của tam giác.
Ví dụ
Tìm diện tích tam giác ABC có độ dài đáy BC là 12cm và chiều cao h là 5cm.
Câu trả lời:
Áp dụng công thức tính diện tích tam giác, diện tích tam giác ABC là:
S = ½ x 12 x 5 = 30 (cm²).
TAM GIÁC ĐỀU
Định nghĩa
Tam giác đều là tam giác có 3 cạnh bằng nhau, 3 đường cao bằng nhau, 3 trung tuyến bằng nhau, 3 đường phân giác bằng nhau và 3 góc bằng nhau bằng 60o.
Thiên nhiên
– Nếu một tam giác có 3 góc bằng nhau thì tam giác đó là tam giác đều.
Nếu một tam giác cân có một góc 60o thì tam giác đó là tam giác đều.
Trong một tam giác đều, mỗi góc là 60o.
Tam giác có 3 cạnh bằng nhau là tam giác đều
Tam giác có 3 góc bằng nhau là tam giác đều
Tam giác có 2 góc bằng 60o là tam giác đều.
Công thức tính chu vi tam giác đều
Chu vi của một tam giác đều bằng 3 lần cạnh bất kỳ của tam giác.
Chu vi P = 3a
Trong đó:
+ P là Chu vi tam giác đều
+ a là độ dài cạnh của tam giác.
Công thức tính diện tích tam giác đều
Diện tích tam giác đều bằng độ dài chiều cao nhân với đáy thì chia cho 2 là bao nhiêu.
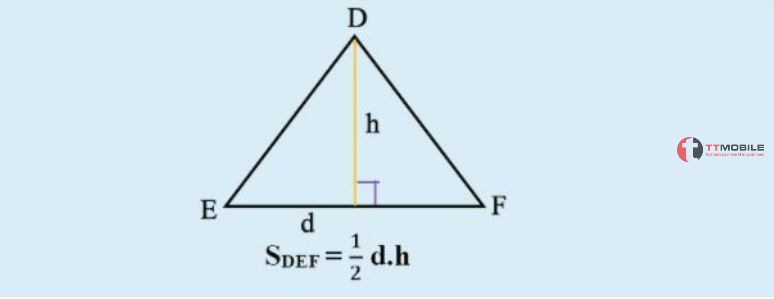
Công thức tính diện tích tam giác đều S = (axh) / 2.
Trong đó:
+ a là độ dài cạnh đáy của tam giác đều, đáy là một trong 3 cạnh của tam giác, cạnh đáy là cạnh đáy.
+ h là chiều cao của tam giác, chiều cao này là đoạn thẳng từ đỉnh xuống đáy của tam giác.
Ví dụ
Cho tam giác đều DEF, chiều cao 8cm và chiều dài đáy là 4cm. Tính diện tích tam giác đều DEF?
Câu trả lời:
Gọi h là đường cao nối từ đỉnh D đến cạnh đáy EF và d là độ dài cạnh đáy EF.
Áp dụng công thức tính diện tích tam giác đều ta có diện tích tam giác đều DEF là: S = ½ x 4 x 8 = 16 (cm²).
TAM GIÁC VUÔNG
Định nghĩa
Tam giác vuông là tam giác có góc vuông 90 độ.
Thiên nhiên
– Tam giác có một góc vuông là tam giác vuông
– Tam giác có hai góc nhọn phụ nhau là tam giác vuông
– Tam giác có đường trung tuyến ứng với một cạnh bằng nửa cạnh đó là tam giác vuông.
Một tam giác có bình phương của một cạnh bằng tổng bình phương của hai cạnh còn lại là tam giác vuông.
– Một tam giác nội tiếp đường tròn có một cạnh là đường kính của đường tròn đó là tam giác vuông.
Công thức tính chu vi tam giác vuông
Chu vi tam giác vuông P = a + b + c
Trong đó:
A, b, c là độ dài ba cạnh của tam giác
Công thức tính diện tích tam giác vuông
Trong tam giác vuông, nếu một cạnh của góc vuông được coi là đáy thì cạnh còn lại là chiều cao. Diện tích hình tam giác bằng chiều dài cơ sở nhân với chiều cao tương ứng rồi chia cho 2.
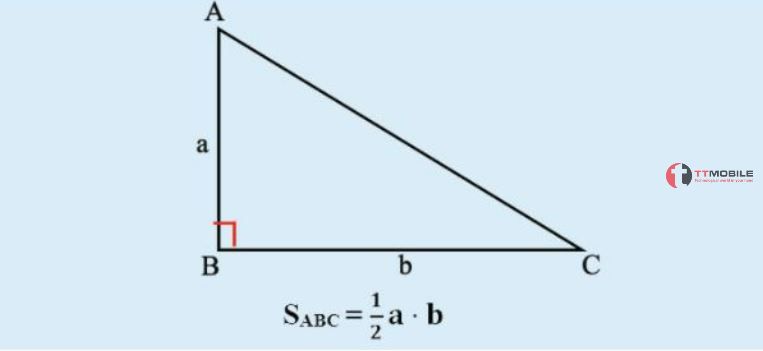
Hoặc:
Diện tích của một tam giác vuông bằng 1/2 tích của chiều cao và chiều dài của đáy.
Công thức S = xaxb
Trong đó:
+ a là đường cao của tam giác.
+ b là cạnh đáy của tam giác.
Ví dụ
Tìm diện tích tam giác vuông ABC có chiều cao 20cm và chiều dài đáy là 30cm.
Câu trả lời:
Áp dụng công thức tính diện tích tam giác vuông ta có diện tích tam giác vuông ABC là:
S = ½ x 20 x 30 = 300 (cm²).
TAM GIÁC QUYỀN ANGLE
Định nghĩa
Tam giác vuông cân là tam giác có hai cạnh bên bằng nhau và vuông góc.
Thiên nhiên
Một tam giác vuông cân có 2 góc ở đáy bằng và 45 độ.
– Các đường cao, trung tuyến và đường phân giác vẽ từ đỉnh của góc vuông của tam giác cân trùng nhau và là nửa cạnh huyền.
Đặc biệt:
Có tam giác ABC cân tại A. Gọi D là trung điểm của BC. Khi đó, aD là đường cao, đồng thời là phân giác và trung trực của BC.
AD = BD = DC = 1/2 BC.
Công thức tính diện tích tam giác cân
Tam giác vuông cân là tam giác có một góc vuông, cùng chiều cao và đáy. Vì vậy:
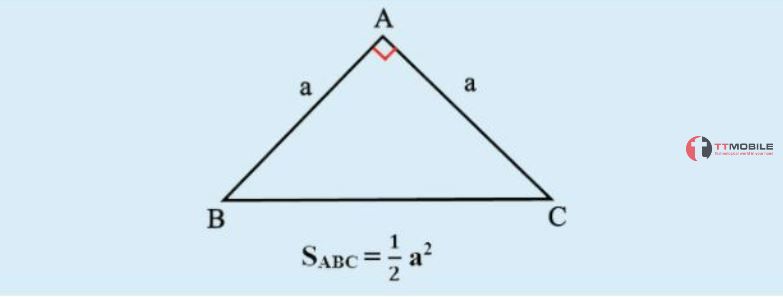
Diện tích của một tam giác đều bằng ½ tích của các bình phương có độ dài của đáy hoặc góc vuông.
Công thức: S = x a²
trong đó a là độ dài cạnh đáy của tam giác.
Ví dụ
Tìm diện tích tam giác ABC cân tại A, cho biết độ dài cạnh AB là 8cm.
Câu trả lời:
Áp dụng công thức tính diện tích tam giác vuông cân, diện tích tam giác ABC là:
S = ½ x 8² = 32 (cm²).
TAM GIÁC CÂN
Định nghĩa
Tam giác cân là tam giác có 2 cạnh bằng nhau và số đo góc ở đáy bằng nhau.
Thiên nhiên
Trong một tam giác cân, 2 cạnh đồng dư và 2 góc đáy đồng dư.
Tam giác vuông cân là tam giác vuông có hai cạnh bên hoặc hai góc ở đáy bằng nhau.
– Đường cao từ đỉnh đến đáy của một tam giác cân cũng là đường trung tuyến và đường phân giác của tam giác đó.
Công thức tính chu vi của tam giác cân
Chu vi của một tam giác cân đồng dạng với một tam giác thường.
P = a + b + c
Trong đó:
P là chu vi của tam giác
a, b, c lần lượt là độ dài 3 cạnh của tam giác đó.
Công thức tính diện tích tam giác cân
Tam giác cân là tam giác có hai cạnh bằng nhau. Hai cạnh này được gọi là hai cạnh bên và cạnh còn lại là cạnh đáy.
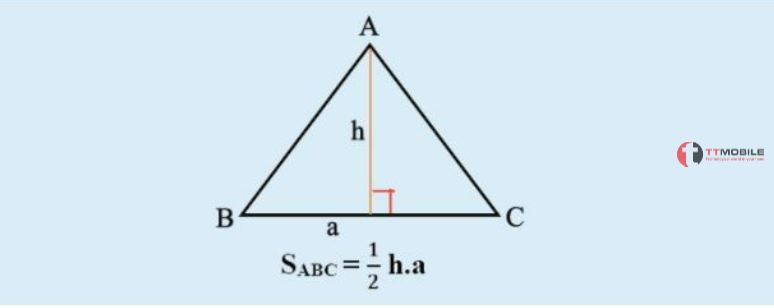
Diện tích tam giác cân tương tự như diện tích tam giác đều, bằng ½ tích của đường cao nối đỉnh nhân với cạnh đáy của tam giác.
Công thức: S = xaxh
Trong đó:
h: Chiều cao ghép từ đỉnh và vuông góc với đáy của tam giác.
a: Độ dài cạnh đáy của tam giác.
Ví dụ
Cho ABC là tam giác cân tại A, có chiều cao là 12cm và chiều dài đáy là 5cm. Tính diện tích tam giác cân ABC?
Câu trả lời:
Áp dụng công thức tính diện tích tam giác cân, diện tích tam giác cân ABC là:
S = ½ x 12 x 5 = 30 (cm²).
ĐIỀU KIỆN VÙNG TAM GIÁC NÂNG CAO
Ngoài những công thức diện tích tam giác cơ bản ở trên, vẫn còn những công thức diện tích tam giác nâng cao hơn. Một trong số đó phải kể đến 3 công thức: Công thức tính diện tích tam giác bằng công thức Heron, công thức tính diện tích tam giác bằng hàm lượng giác và công thức tính diện tích Một tam giác bằng một góc.
Công thức tính diện tích tam giác khi biết một góc
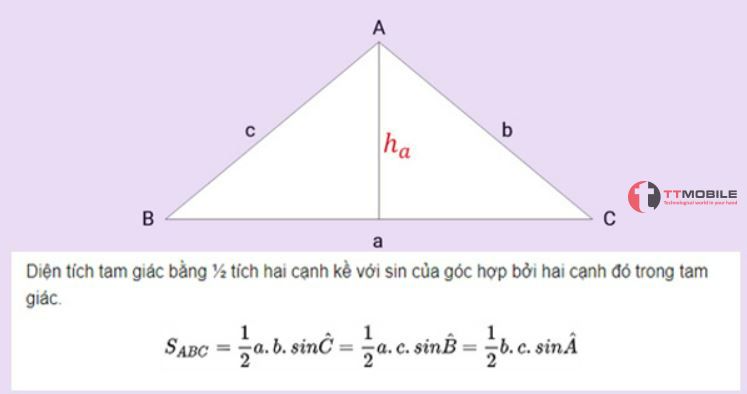
– Công thức tính diện tích hình tam giác theo Cô-li-a. công thức
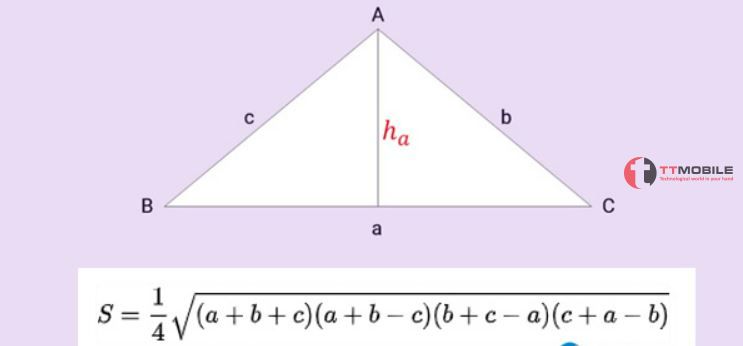
– Công thức tính diện tích tam giác kéo dài
Để có thể áp dụng công thức tính diện tích tam giác kéo dài này, trước hết bạn cần chứng minh được điều đó rồi mới sử dụng công thức tính.
+ Công thức 1:

Trong đó:
– a, b, c: Độ dài cạnh của tam giác
– R: Bán kính đường tròn ngoại tiếp tam giác
+ Công thức 2:

Trong đó:
– p: nửa chu vi hình tam giác
– r: bán kính đường tròn nội tiếp tam giác
Xem thêm:
- Tổng hợp 5 công thức tính diện tích tam giác đều, vuông, cân
- 3 Công thức tính diện tích hình thang
- Tổng hợp công thức lượng giác lớp 9,10,11,12 Full
Bản tóm tắt
TTmobile vừa liệt kê cho các bạn 9 công thức tính diện tích tam giác từ cơ bản đến nâng cao. Hi vọng từ những chia sẻ của bài viết sẽ giúp các bạn có thêm những thông tin hữu ích để học tập. Cảm ơn bạn rất nhiều vì đã xem và đọc.
Bạn thấy bài viết 9 Công Thức Tính Diện Tích Tam Giác đáng chú ý có giải quyết đươc vấn đề bạn tìm hiểu không?, nếu không hãy comment góp ý thêm về 9 Công Thức Tính Diện Tích Tam Giác đáng chú ý bên dưới để tmdl.edu.vn có thể chỉnh sửa & cải thiện nội dung tốt hơn cho độc giả nhé! Cám ơn bạn đã ghé thăm Website Trường Trung Cấp Nghề Thương Mại Du Lịch Thanh Hoá
Chuyên mục: Hỏi đáp
Nguồn: tmdl.edu.vn
Trang chủ: tmdl.edu.vn
Danh mục bài: Tổng hợp




