Ngoài các công thức tính diện tích hình vuông, hình chữ nhật, hình tròn, bài viết dưới đây Trung Cấp Nghề Thương Mại Du Lịch Thanh Hoá sẽ hướng dẫn các ví dụ cụ thể giúp bạn tính diện tích hình thoi, chu vi hình thoi để các bạn hiểu toán hơn.
Trong hướng dẫn công thức tính chu vi và diện tích tmdl.edu.vn dưới đây sẽ cung cấp cho các bạn công thức tính diện tích chính xác nhất kèm theo các ví dụ cụ thể để các bạn dễ dàng nắm bắt kiến thức và vận dụng vào thực tế.
Công thức tính diện tích và chu vi hình thoi
1. Hình thoi là gì?
Hình thoi là tứ giác có 4 cạnh bằng nhau. Hình thoi cũng là hình bình hành có 2 cặp cạnh kề đồng dạng hoặc hình bình hành có 2 đường chéo vuông.
Thuộc tính kim cương:
Hình thoi có tất cả các tính chất của hình bình hành.
– Hai đường chéo vuông góc với nhau.
Hai đường chéo là đường phân giác của hình thoi.
Dấu hiệu nhận biết hình thoi:
Một tứ giác có 4 cạnh bằng nhau.
– Hình bình hành có hai cạnh đồng dạng.
Một hình bình hành có hai đường chéo vuông góc với nhau.
– Hình bình hành có một đường chéo là đường phân giác một góc.
2. Công thức tính diện tích hình thoi
– Khái niệm tính diện tích hình thoi: Diện tích hình thoi bằng một nửa (1/2) tích độ dài hai đường chéo.
* Công thức tính toán dựa trên đường chéo
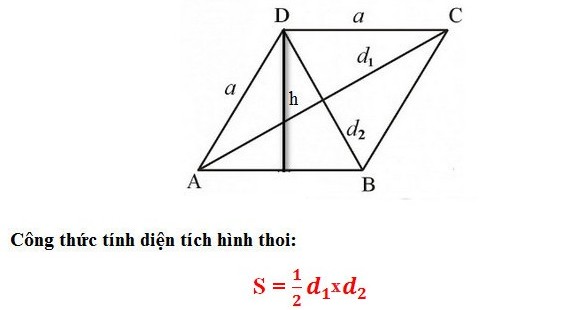
Ở đó:
+ d1 : đường chéo đầu tiên.
+ d2 : đường chéo thứ hai.
– Ví dụ:
DV1. Xét một hình thoi có các đường chéo lần lượt là 7 cm và 9 cm. Diện tích của hình thoi này là bao nhiêu?
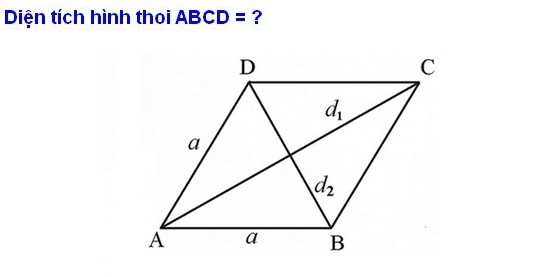
Áp dụng phép tính diện tích hình thoi ta được d1 = 7 cm và d2 = 9 cm. Chúng tôi đặt công thức và nhận được kết quả sau:
S = 1/2 x (d1 x d2) = 1/2 x (7 x 9) = 1/2 x 63 = 31,5 (cm)hai).
DV2: Tìm diện tích hình thoi có các đường chéo lần lượt là 9 cm và 8 cm.
Phần thưởng:
Áp dụng công thức tính các đường chéo của hình thoi d1 = 9cm, d2 = 8cm, ta có:
S = 1/2 x (d1 x d2) = 1/2 (9 x 8) = 1/2 x 72 = 36 1,5 (cm.)hai).
* Công thức tính diện tích hình thoi theo cơ sở và chiều cao
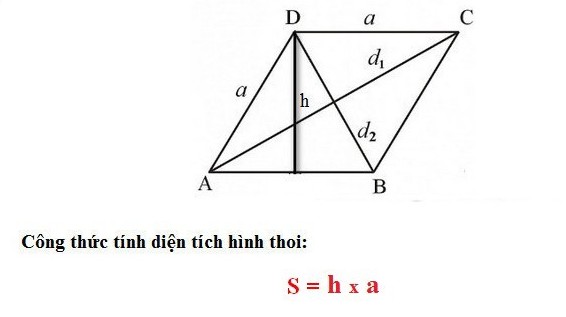
Ở đó:
– h: Chiều cao của hình thoi.
– a: Cạnh dưới.
Ví dụ: Cho hình thoi ABCD, cạnh AB = BC = CD = DA = 4 cm, chiều cao của hình thoi là 3 cm. Tính diện tích của hình thoi.
Phần thưởng: Áp dụng công thức tính diện tích hình thoi ta được h = 3cm, a = 4cm. Chúng tôi thay thế công thức và nhận được kết quả sau:
S = axh = 3 x 4 = 12 1,5 (cm.)hai).
* Công thức tính diện tích hình thoi dựa vào quan hệ trong tam giác (Nhập góc của hình thoi)
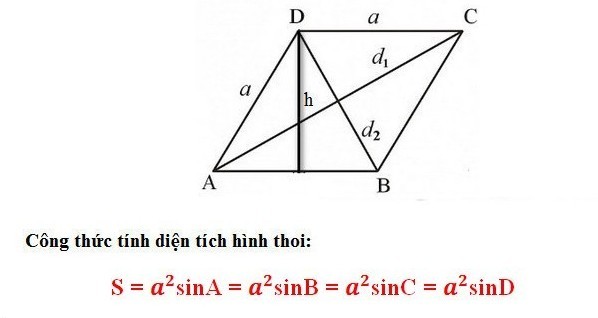
Trong đó: a: cạnh của hình thoi
Ví dụ: Cho hình thoi ABCD, cạnh hình thoi = 4cm, góc A = 35 độ. Tìm diện tích của hình thoi ABCD.
Phần thưởng: Áp dụng công thức, ta được a = 4, góc = 35 độ. Chúng tôi thay thế công thức sau:
S = mộthai x sinA = 4hai x sin (35Cái này) = 9.177 (cmhai).
Quan sát:
Đơn vị diện tích của hình thoi là m.haicentimethai…
– Khi tính toán phải đảm bảo rằng các đơn vị mà bài toán đưa ra là giống nhau. Nếu không, bạn phải chuyển đổi sang cùng một đơn vị trước khi thực hiện việc này.
3. Công thức tính chu vi hình thoi.
– Khái niệm tính chu vi hình thoi: Chu vi hình thoi được tính bằng cách nhân độ dài một cạnh với 4. Số 4 ở đây được hiểu là 4 cạnh của hình thoi.
– Công thức tính chu vi hình thoi:
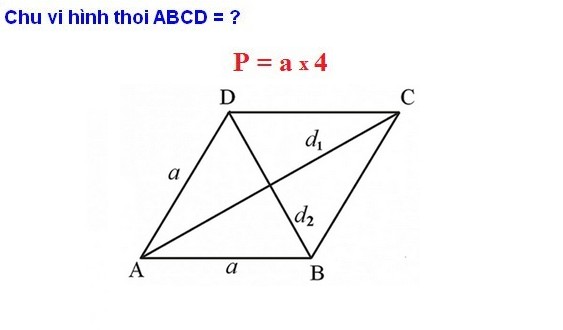
Ở đó:
+ P: Chu vi của hình thoi.
+ một: Bất kỳ cạnh nào của hình thoi.
– Ví dụ: Cho hình thoi ABCD có cạnh là 7 cm. Chu vi của hình thoi này là bao nhiêu?
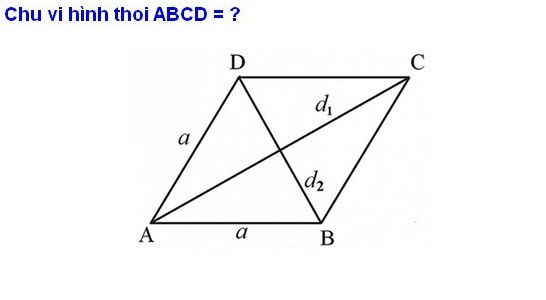
Theo công thức tính chu vi hình thoi đã trình bày ở trên, ta có = 7 cm. Như vậy, chu vi hình thoi ABCD sẽ được tính như sau:
P (ABCD) = trục 4 = 7 x 4 = 28 (cm).
4. Công thức tính đường chéo của hình thoi.
Dựa vào các công thức tính chu vi hình thoi, diện tích hình thoi ở trên, chúng ta có thể dễ dàng tìm được công thức tính đường chéo của hình thoi như sau:
* Tính đường chéo, diện tích và độ dài 1 đường chéo của hình thoi đã cho:
Nếu biết diện tích hình thoi, độ dài đường chéo (d1), ta dễ dàng tìm được đường chéo còn lại của hình thoi bằng công thức: d2 = 2S / d1.
5. Bài tập về diện tích và chu vi hình thoi
Bài 1: Cho hình thoi ABCD có cạnh AD = 4m và góc DAB = 30 độ. Tìm diện tích của hình thoi ABCD.
Phần thưởng:
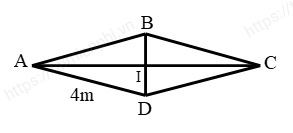
Vì ABCD là hình thoi nên các tam giác thu được là các tam giác cân, lấy trung điểm của hai đường chéo thì AI vuông góc với BD, góc IAB = 15 độ.
Vậy AI = AB. vì IAB = 4. Cos 15 = 3,86 (m).
Xét tam giác vuông ABI, theo định lý Pitago, ta có:
MỘThai= ABhai– trí tuệ nhân tạohai= 4hai – 3,86hai = 1,1 (m).
Vậy BI = 1,05m
- CA = 2. AI = 7.72m
- BD = 2. BI = 2,1 m
Dựa vào công thức tính diện tích hình thoi ta có diện tích hình thoi ABCD = ½. ĐÂY. DB = 8.106 (mhai)
Bài 2: Tìm diện tích hình thoi ABCD biết AB = 5cm, đường chéo AC = 8cm.
Phần thưởng:
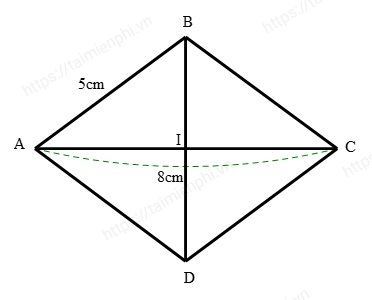
Gọi nó là giao điểm của AC và BD, ta có AI = IC = 4cm.
Xét tam giác vuông ABI, ta có:
MỘThai= ABhai– trí tuệ nhân tạohai
Thay AI = 4cm, AB = 5cm, ta được: BI = 3cm.
Mà BD = 2.BI = 2.3 = 6cm.
Diện tích hình thoi ABCD: S = (BD. AC): 2 = 6,8: 2 = 24 (cm)hai).
Bài 3: Tìm diện tích của một hình thoi có cạnh là 60 °.
Phần thưởng
Khi tính diện tích hình thoi biết cạnh a và góc 60o, ta có 2 cách sau:
Cách 1: Để tính diện tích hình thoi mà không cần học lượng giác lớp 8 chúng ta áp dụng phương pháp giải sau:
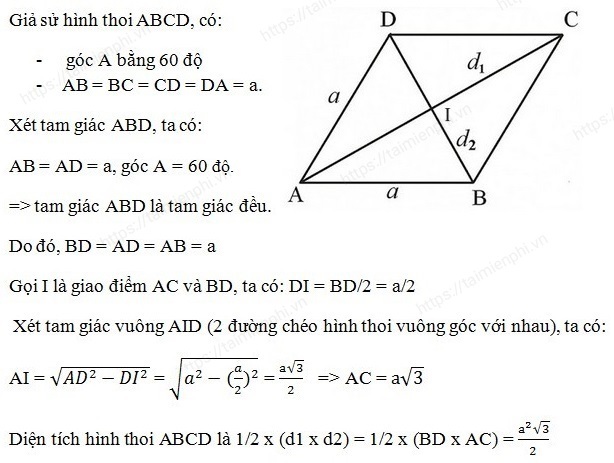
Cách 2: Tính diện tích hình thoi bậc 12, bậc 9, 10, 11 bằng công thức lượng giác
Diện tích của hình thoi có cạnh a và góc 60o là:
S = mộthaisin A = mộthai.sin (600) = 0,866ahai
—————– HẾT ———————
Đây là dạng toán nâng cao về hình thang. Với dạng bài toán này, chúng ta cần kết hợp các đặc điểm về góc và cạnh của hình thang ở trên để tìm ra đáp án.
Với công thức tính chu vi hình thoi và diện tích hình thoi trên đây, chắc chắn bạn đọc đã có được những thông tin hữu ích và quan trọng trong bài học trong việc giải các câu hỏi, bài toán từ đơn giản đến khó. hoặc cuộc sống. Tuy nhiên, cũng cần lưu ý mối tương quan giữa các thành phần trong công thức tính chu vi và diện tích hình thoi. Vì sẽ có những bài toán yêu cầu bạn áp dụng cách tính chu vi và diện tích của hình thoi để tìm ra đáp số và ẩn số còn thiếu.
#Công #thức #tính #diện #tích #hình #thoi #chu #hình #thoi #cách #tính
Trang chủ: tmdl.edu.vn
Danh mục bài: Toán học