Đường trung tuyến là một mảng kiến thức vô cùng quan trọng đối với môn Toán. Vậy đường trung tuyến là gì? Các tính chất của đường trung tuyến ra sao và được áp dụng như thế nào trong bài tập? Hãy cùng Tmdl.edu.vn tìm hiểu ngay nhé.
Đường trung tuyến là gì?
Trong toán học, đường trung tuyến của một đoạn thẳng là một đường thẳng đi qua trung điểm của đoạn thẳng đó.
Bạn đang xem bài: Đường Trung Tuyến Là Gì? 3 Định Lý Về đường Trung Tuyến
Định nghĩa đường trung tuyến trong tam giác
Đường trung tuyến trong tam giác là một đoạn thẳng nối từ đỉnh của tam giác tới trung điểm của cạnh đối diện. Mỗi tam giác sẽ có 3 đường trung tuyến.
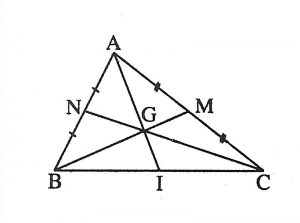
Chẳng hạn như, theo như hình vẽ trên thì các đoạn thẳng AI, CN, BM sẽ là 3 trung tuyến của tam giác ABC.
Định nghĩa đường trung tuyến trong tam giác đặc biệt
Tính chất đường trung tuyến trong tam giác vuông
Đối với tam giác vuông đường trung tuyến của tam giác bao gồm 3 tính chất đó là:
- Trong một tam giác vuông, đường trung tuyến ứng với cạnh huyền bằng nửa cạnh huyền.
- Một tam giác có trung tuyến ứng với một cạnh bằng nửa cạnh đó thì tam giác ấy là tam giác vuông.
- Tam giác ΔABC vuông ở A, độ dài đường trung tuyến AM sẽ bằng MB, MC và bằng BC. Ngược lại nếu AM = BC thì tam giác ΔABC sẽ vuông ở A.
Tính chất đường trung tuyến trong tam giác cân
Trong tam giác cân, đường trung tuyến ứng với cạnh đáy thì vuông góc với cạnh đấy và chia tam giác các thành hai tam giác bằng nhau.
Tính chất đường trung tuyến trong tam giác đều
- 3 đường trung tuyến của tam giác đều sẽ chia tam giác đó thành 6 tam giác có diện tích bằng nhau.
- Trong tam giác đều đường thẳng đi qua một đỉnh bất kỳ và đi qua trọng tâm của tam giác sẽ chia tam giác đó thành 2 tam giác có diện tích bằng nhau.
Tính chất của đường trung tuyến là gì?
- Ba đường trung tuyến của tam giác cùng đi qua một điểm. Điểm đó cách đỉnh một khoảng bằng 2/3 độ dài đường trung tuyến đi qua đỉnh ấy.
- Giao điểm của ba đường trung tuyến gọi là trọng tâm.
- Vị trí của trọng tâm tam giác: Trọng tâm của một tam giác cách mỗi đỉnh một khoảng bằng 2/3 độ dài đường trung tuyến đi qua đỉnh ấy.
Ví dụ:

Gọi G là trọng tâm của tam giác ABC, ABC có các trung tuyến AI, BM, CN thì ta sẽ có biểu thức:
định lý đường trung tuyến
Nếu đường trung tuyến trong tam giác có 3 tính chất thì định lí của đường trung tuyến cũng có 3 định lí đó là:
- Định lí 1: Ba đường trung tuyến của một tam giác cùng đi qua một điểm. gọi là trọng tâm của tam giác đó.
- Định lí 2: Đường trung tuyến của tam giác chia tam giác ấy thành hai tam giác có diện tích bằng nhau. Ba trung tuyến chia tam giác thành 6 tam giác nhỏ với diện tích bằng nhau.
- Định lí 3: Về vị trí trọng tâm: Trọng tâm của một tam giác cách mỗi đỉnh một khoảng bằng độ dài đường trung tuyến qua đỉnh ấy.
Công thức đường trung tuyến
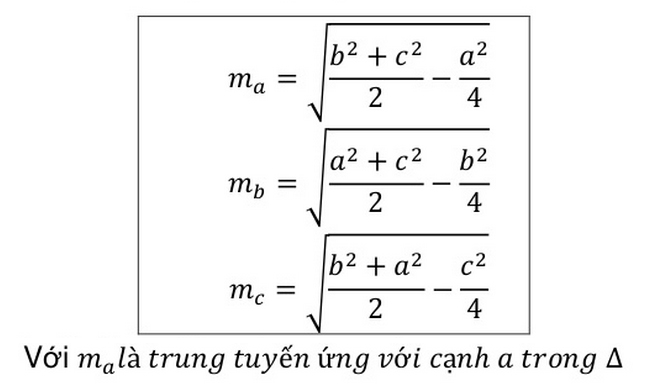
Độ dài đường trung tuyến của một tam giác được tính thông qua độ dài các cạnh của tam giác và được tính bằng định lý Apollonnius:
Các dạng bài thường gặp về đường trung tuyến
Bài tập 1: Cho tam giác ABC có M,N lần lượt là trung điểm của các cạnh AB, AC. Hãy chứng minh tam giác ABC cân tại A.
Lời giải:
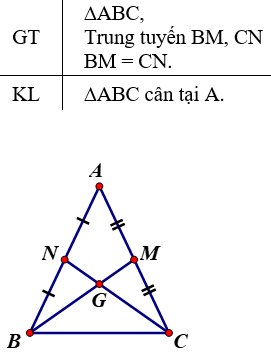
Vì BM và CN là hai đường trung tuyến của tam giác ABC mà BM giao CN tại G, nên ta có:
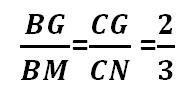
Mà BM = CN nên BG = CN và GN = GM
Xét ΔBNG và ΔCGM ta có:
˄BGN = ˄CGM (2 góc đối đỉnh)
- → ΔBNG đồng dạng với ΔCMG
- → BN = CM (1)
Mà M và N lần lượt là trung điểm của AB và AC (2)
Từ (1) và (2) ta có: AB = AC => Tam giác ABC cân tại A (đpcm).
Bài tập 2: Cho ΔABC có BM, CN là hai đường trung tuyến cắt nhau tại G. Kéo dài BM lấy đoạn ME=MG. Kéo dài CN lấy đoạn NF=NG. Chứng minh:
- EF=BC
- Đường thẳng AG đi qua trung điểm BC.
Lời giải:
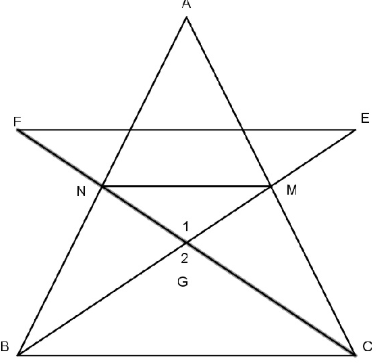
a.) Ta có BM và CN là hai đường trung tuyến gặp nhau tại G nên G là trọng tâm của tam giác ΔABC.
⇒GC=2GN
mà FG=2GN⇒GC=GF
Tương tự BG, GE và ^G1=^G2 (đđ). Do đó ΔBGC=ΔEGF(c.g.c)
Suy ra BC=EF
b.) G là trọng tâm nên AG chính là đường trung tuyến thứ ba trong tam giác ABC.
nên AG đi qua trung điểm của BC.
Xem thêm:
Như vậy qua bài viết trên đây, chúng ta đã có bổ sung kiến thức và ôn tập lại lí thuyết về đường trung tuyến là gì. Hi vọng với những kiến thức bổ ích này sẽ giúp các bạn có thể rèn luyện lại kiến thức cho mình một cách tốt nhất và hiệu quả nhất. Hãy like, share để để cùng lan tỏa kiến thức với Tmdl.edu.vn nhé.
Trang chủ: tmdl.edu.vn
Danh mục bài: Tổng hợp