Các dạng bài tập toán có chứa dấu giá trị tuyệt đối thường gây bối rối cho nhiều em học sinh vì thường phải chia điều kiện, kết luận nghiệm phải đối chiếu điều kiện khi khử (phá) dấu trị tuyệt đối.
Vậy làm sao để giải các dạng bài tập giá trị tuyệt đối chính xác? Chắc chắn chúng ta phải rèn kỹ năng giải toán bằng cách làm thật nhiều bài tập dạng này. Bài viết này chúng ta cùng ôn lại các dạng toán giá trị tuyệt đối ở chương trình toán lớp 7.
Bạn đang xem bài: Các dạng Bài tập Giá trị tuyệt đối và Cách giải – Toán lớp 7
I. Kiến thức về Giá trị tuyệt đối cần nhớ
• Nếu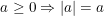 
• Nếu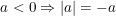 
• Nếu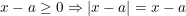 
• Nếu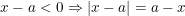 
* Chú ý: Giá trị tuyệt đối của mọi số đều không âm: |a|≥0 với mọi a∈R.
• Hai số bằng nhau hoặc đối nhau thì có giá trị tuyệt đối bằng nhau. Ngược lại hai số có giá trị tuyệt đối bằng nhau thì chúng là hai số bằng nhau hoặc đối nhau. Tức là:
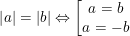
• Mọi số đều lớn hơn hoặc bằng đối của giá trị tuyệt đối của nó và đồng thời nhỏ hơn hoặc bằng giá trị tuyệt đối của nó. Tức là:
và 
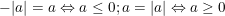
• Trong hai số âm, số nào nhỏ hơn thì có giá trị tuyệt đối lớn hơn:
a<b<0⇒|a|>|b|
• Trong hai số dương, số nào nhỏ hơn thì có giá trị tuyệt đối nhỏ hơn:
0<a<b⇒|a|<|b|
• Giá trị tuyệt đối của một tích bằng tích các giá trị tuyệt đối:
|a.b|=|a|.|b|
• Giá trị tuyệt đối của một thương bằng thương hai giá trị tuyệt đối:
• Bình phương của giá trị tuyệt đối của một số bằng bình phương số đó:
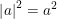
• Tổng hai giá trị tuyệt đối của hai số luôn lớn hơn hoặc bằng giá trị tuyệt đối của hai số, dấu bằng xảy ra khi và chỉ khi hai số cùng dấu:
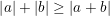và 
II. Các dạng Bài tập Giá trị tuyệt đối
° Dạng 1: Rút gọn biểu thức và tính giá trị của biểu thức
* Ví dụ 1: Tính |x| biết:
a)
b)
c)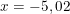
* Lời giải:
a)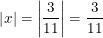
b)
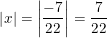c)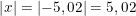
* Ví dụ 2 (bài 17 trang 15 SGK Toán 7 tập 1). Tìm x biết:
a)
b)
c)
d)
* Lời giải:
a)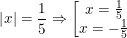
b)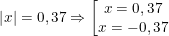
c)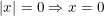
d)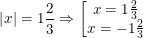
* Ví dụ 3: Tính giá trị của biểu thức
a)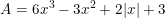 
với x = -2/3
b)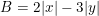 
với x =1/2; y =-3;
* Lời giải:
a) Ta có: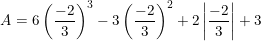 
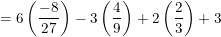
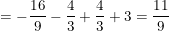
b) Ta có: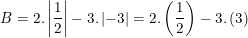 
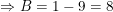
* Ví dụ 4: Rút gọn biểu thức sau với 3,5≤x≤4,5
a) A = |x – 3,5| + |4,5 – x|
b) B = |-x + 3,5| + |x – 4,5|
* Lời giải:
a) Vì x≥3,5 ⇒ x – 3,5 ≥ 0 nên |x – 3,5| = x – 3,5
vì x≤4,5 ⇒ 4,5 – x ≥ 0 nên |4,5 – x| = 4,5 – x;
⇒ A = (x – 3,5) + (4,5 – x) = 1
b) Vì x≥3,5 ⇒ – x + 3,5 ≤ 0 nên |-x + 3,5| = – (-x + 3,5) = x – 3,5.
vì x≤4,5 ⇒ x – 4,5 ≤ 0 nên |x – 4,5| = -(x – 4,5) = 4,5 – x.
⇒ B = (x – 3,5) + (4,5 – x) = 1.
° Dạng 2: Tìm giá trị của x trong bài toán dạng |A(x)| = k
* Phương pháp giải:
• Để tìm x trong bài toán dạng |A(x)| = k, (trong đó A(x) là biểu thức chứa x, k là 1 số cho trước) ta làm như sau:
– Nếu k < 0 thì không có giá trị nào của x thỏa mãn đẳng thức (trị tuyệt đối của mọi số đều không âm).
– Nếu k = 0 thì ta có |A(x)| = 0 ⇒ A(x) = 0
– Nếu k > 0 thì ta có: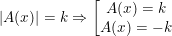 
* Ví dụ 1: Tìm x biết:
a)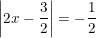
b)
* Lời giải:
a) Vì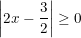 
nên không có giá trị nào của x thỏa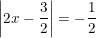
b)
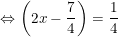hoặc 
• TH1: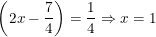 
• TH2: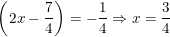 
– Kết luận: Có 2 giá trị của x thỏa điều kiện là x = 1 hoặc x = 3/4.
* Ví dụ 2 (Bài 25 trang 16 SGK Toán 7 Tập 1): Tìm x biết:
a)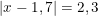
b)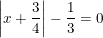
* Lời giải:
a)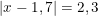
– Vậy có 2 giá trị x thỏa yêu cầu bài toán là x = 4 hoặc x = -0,6.
b)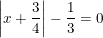 
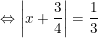
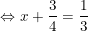hoặc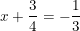 
• Nếu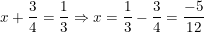 
• Nếu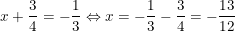 
– Kết luận: Vậy x = -5/12 hoặc x = -13/12 thỏa.
° Dạng 3: Tìm giá trị của x trong bài toán dạng |A(x)| = |B(x)|
* Phương pháp giải:
• Để tìm x trong bài toán dạng dạng |A(x)| = |B(x)|, (trong đó A(x) và B(x)là biểu thức chứa x) ta vận dụng tính chất sau:
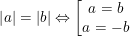tức là: 
* Ví dụ: Tìm x biết:
a)|5x – 4| = |x + 4|
b)|7x – 1| – |5x + 1| = 0
* Lời giải:
a)|5x – 4| = |x + 4|
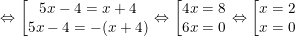
– Vậy x = 2 và x = 0 thỏa điều kiện bài toán
b)|7x – 1| – |5x + 1| = 0 ⇔ |7x – 1| = |5x + 1|
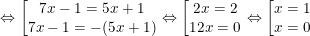
– Vậy x = 1 và x = 0 thỏa điều kiện bài toán.
° Dạng 4: Tìm giá trị của x trong bài toán dạng |A(x)| = B(x)
* Phương pháp giải:
• Để tìm x trong bài toán dạng |A(x)| = B(x) (*), (trong đó A(x) và B(x)là biểu thức chứa x) ta thực hiện 1 trong 2 cách sau:
* Cách giải 1:
1- Điều kiện B(x)≥0
2- Khi đó (*) trở thành 
3- Tìm x rồi đối chiếu x với điều kiện B(x)≥0 rồi kết luận.
* Cách giải 2: Chia khoảng xét điều kiện để khử (bỏ) trị tuyệt đối
– TH1: Nếu A(x)≥0 thì (*) trở thành A(x) = B(x) (sau khi tìm được x đối chiếu x với điều kiện A(x)≥0)
– TH2: Nếu A(x)<0 thì (*) trở thành -A(x) = B(x) (sau khi tìm được x đối chiếu x với điều kiện A(x)<0)
* Ví dụ: Tìm x biết:
a)|x – 3| = 5 – 2x b)|5 – x| = 3x + 1
° Lời giải:
a)|x – 3| = 5 – 2x (*)
* Giải theo cách 1:
– Điều kiện 
ta có:
(*) trở thành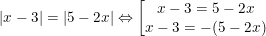 
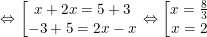
– Đối chiếu với điều kiện x≤5/2 thì chỉ có x=2 thỏa, x = 8/3 loại
– Kết luận: Vậy x = 2 là giá trị cần tìm.
* Giải theo cách 2:
¤ TH1: (x – 3) ≥ 0 ⇒ x ≥ 3. Ta có:
(*) trở thành (x – 3) = 5 – 2x ⇒ 3x = 8 ⇒ x = 8/3
Đối chiếu điều kiện ta thấy x = 8/3 < 3 nên loại.
¤ TH2: (x – 3) < 0 ⇒ x < 3. Ta có:
(*) trở thành -(x – 3) = 5 – 2x ⇒ -x + 3 = 5 – 2x ⇒ x = 2
Đối chiếu điều kiện ta thấy x = 2 < 3 nên nhận.
– Kết luận: Vậy x = 2 là giá trị cần tìm.
* Nhận xét: Ở dạng này thường giải theo cách 1 bài toán gọn hơn, các em lưu ý đối chiếu lại giá trị x tìm được với điều kiện.
III. Một số bài tập về giá trị tuyệt đối
– Vận dụng phương pháp giải các dạng toán trị tuyệt đối ở trên các em hãy làm các bài tập sau:
* Bài 1: Rút gọn biểu thức với x < -1,5
a) A = |x + 1,5| – |x – 2,5|
b) B = |-x – 1,5| + |x – 3,5|
* Bài 2: Rút gọn biểu thức sau
a) A = |x – 2,2| + |x – 1,8|
b) B = |-x – 1,4| + |x – 2,6|
* Bài 3: Tìm x, biết:
a) 
b)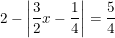
* Bài 4: Tìm x, biết:
a)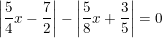
b)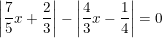
* Bài 5: Tìm x, biết:
a) |4 + 2x| + 4x = 0
b) |3x – 7| – 1 = 2x
Đến đây có lẽ các em đã nắm được cơ bản tính chất của trị tuyệt đối cách vận dụng giải một số bài toán tìm x trong bài toán có dấu trị tuyệt đối.
Thực tế còn khá nhiều bài toán dựa vào tính không âm của trị tuyệt đối như tìm giá trị lớn nhất, giá trị nhỏ nhất của biểu thức và các bài toán hỗn hợp khác mà có thể Trường Trung Cấp Nghề Thương Mại Du Lịch Thanh Hoá sẽ cập nhật sau.
Hy vọng với bài viết về các dạng bài tập về giá trị tuyệt đối và cách giải ở trên giúp ích cho các em. Mọi thắc mắc và góp ý các em hãy để lại bình luận dưới bài viết để Trường Trung Cấp Nghề Thương Mại Du Lịch Thanh Hoá ghi nhận và hỗ trợ, chúc các em học tốt.
tmdl.edu.vn. Mọi hành vi sao chép đều là gian lận!
Nguồn chia sẻ: https://tmdl.edu.vn/cac-dang-bai-tap-gia-tri-tuyet-doi-va-cach-giai/
Trang chủ: tmdl.edu.vn
Danh mục bài: Giáo dục
