Chia đơn thức cho đơn thức lớp 8: Lý thuyết và các dạng toán

Chia đơn thức cho đơn thức lớp 8: Lý thuyết và các dạng toán

Chia đơn thức cho đơn thức là phần kiến thức quan trọng học sinh đã được tìm hiểu trong chương trình Toán 8, phân môn Đai số. Bài viết hôm nay, Trường Trung Cấp Nghề Thương Mại Du Lịch Thanh Hoá sẽ tổng hợp lại tất cả những kiến thức cần ghi nhớ từ lý thuyết đến các dạng bài tập. Các bạn cùng tìm hiểu nhé !

I. CÁC KIẾN THỨC CẦN GHI NHỚ

Bạn đang xem bài: Chia đơn thức cho đơn thức lớp 8: Lý thuyết và các dạng toán

1. Đơn thức là gì ?

Đơn thức là biểu thức đại số chỉ gồm một số hoặc một biến, một tích giữa các số và các biến.

Ví dụ: 2,3 xy²

3/2x³y²z

2. Quy tắc chia đơn thức cho đơn thức

Với A và B là hai đơn thức, B≠0. Ta nói A chia hết cho B nếu tìm được một đơn thức Q sao cho A = B.Q.

Trong đó:

A là đơn thức bị chia.

B là đơn thức chia.

Q là đơn thức thương (hay gọi là thương)

Kí hiệu: Q = A : B

Quy tắc:

Nhớ lại kiến thức cũ: Ở lớp 7 ta biết: Với x≠0; m, n ∈ N; m ≥ n thì:

x^m : xⁿ = x^{m – n} nếu m>n

x^m : xⁿ = 1 nếu m=n

Muốn chia đơn thức A cho đơn thức B (trường hợp A chia hết cho B) ta làm như sau:

+ Chia hệ số của đơn thức A cho hệ số của đơn thức B.

+ Chia lũy thừa của từng biến trong A cho lũy thừa của cùng biến đó trong B.

+ Nhân các kết quả vừa tìm được với nhau.

Ví dụ: Thực hiện phép tính

a, (- 2)⁵:(- 2)³.

b, (xy²)⁴:(xy²)²

Hướng dẫn:

a) Ta có: (- 2)⁵:(- 2)³ = (- 2)⁵ – 3 = (- 2)² = 4.

b) Ta có: (xy²)⁴:(xy²)² = x⁴y⁸😡²y⁴ = x⁴ – 2.y⁸ – 4 = x²y⁴.

II. CÁC DẠNG BÀI TẬP CHIA ĐƠN THỨC CHO ĐƠN THỨC

Bài 1: Tính (-7)²⁰ : (-7)¹⁸

A. 49     B. –49

C. – 14     D. 14

Đáp án:

Ta có: (-7)²⁰ : (-7)¹⁸ = (-7)²⁰ – 18 = (-7)² = 49

Chọn đáp án A

Bài 2: Kết quả của phép tính (- 3)⁶:(- 2)³ là?

A. 729/8 B. 243/8 C. -729/8 D. -243/8

Ta có: (- 3)⁶:(- 2)³ = 3⁶:(- 2³) = 729:(- 8) = – 729/8.

Chọn đáp án C.

Bài 3: Kết quả nào sau đây đúng?

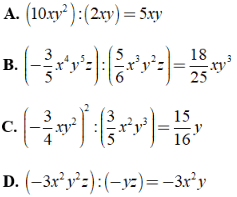
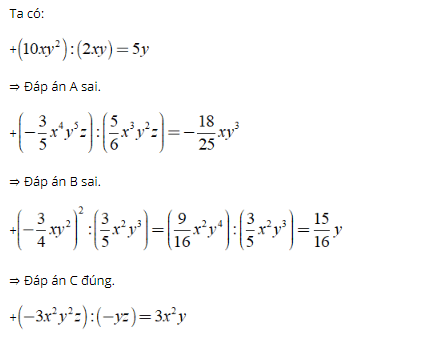
⇒ Đáp án D sai.

Chọn đáp án C.

Bài 4: Chứng mình rằng giá trị của biểu thức sau không phụ thuộc vào giá trị của biến y (x≠0; y≠0) với biểu thức đó là A = 2/3x²y³:(- 1/3xy) + 2x(y – 1)(y + 1)

Hướng dẫn:

Ta có A = 2/3x²y³:(- 1/3xy) + 2x(y – 1)(y + 1) = – 2x² – 1y³ – 1 + 2x(y – 1)(y + 1)

= – 2xy² + 2x(y² – 1) = – 2xy² + 2xy² – 2x = – 2x

⇒ Giá trị của biểu thức A không phụ thuộc vào biến y

Bài 5: Tính giá trị của các biểu thức sau

a) P = 12x⁴y²:(- 9xy²) tại x= -3, y= 1,005.

b) Q = 3x⁴y³:2xy² tại x= 2, y= 1.

Hướng dẫn:

a) Ta có P = 12x⁴y²:(- 9xy²) = 1/2 – 9x⁴ – 1y² – 2 = – 4/3x³

Với x= -3, y= 1,005 ta có P = – 4/3(- 3)³ = 36.

Vậy P = 36

b) Ta có Q = 3x⁴y³:2xy² = 3/2x⁴ – 1y³ – 2 = 3/2x³y.

Với x= 2, y= 1 ta có Q = 3/2( 2 )³.1 = 12.

Vậy Q = 12

Bài 6:

Làm tính chia:

a) 5x²y⁴ : 10x²y;

b) 3/4x³y³ : (-1/2x²y²);

c) (-xy)¹⁰ : (-xy)⁵.

Hướng dẫn giải

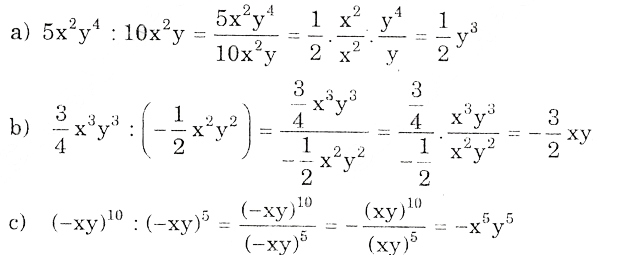
Bài 7: Làm tính chia:

a, 18x²y²z : 6xyz

b, 5a³b : (-2a²b)

c, 27x⁴y²z : 9x⁴y

Lời giải:

a, 18x²y²z : 6xyz = (18 : 6)(x² : x)(y² : y)(z : z) = 3xy

b, 5a³b : (-2a²b) = 5 : (-2)(a³ : a2)(b : b) = – 5/2 a

c, 27x⁴y²z : 9x⁴y = (27 : 9)(x⁴ : x⁴)(y² : y).z = 3yz

Bài 8: Tìm số tự nhiên n để mỗi phép chia sau là phép chia hết:

a, x⁴ : xⁿ

b, xⁿ : x³

c, 5xⁿy³ : 4x³y²

d, xⁿyⁿ⁺¹ : x²y⁵

Lời giải:

x⁴ : xⁿ = x^4-n là phép chia hết nên 4 – n ≥ 0 ⇒ 0 ≤ n ≤ 4

suy ra: n ∈ {0; 1; 2; 3; 4}

xⁿ : x³ = x^{n- 3} là phép chia hết nên n – 3 ≥ 0 ⇒ n ≥ 3

5xny3 : 4x³y² = 54 (xⁿ : x²)(y³ : y²) = 54 x^n-2 là phép chia hết

Suy ra: n – 2 ≥ 0 ⇒ n ≥ 2

xⁿy^{n + 1} : x²y⁵ = (xⁿ : x²)(yⁿ⁺¹ : y⁵) = x^n-2.y^n-4 là phép chia hết

suy ra: n – 4 ≥ 0 ⇒ n ≥ 4

Bài 9: Tính giá trị của biểu thức sau:

(- x²y⁵)² : (- x²y⁵) tại x = 1/2 và y = – 1

Lời giải:

Ta có: (- x²y⁵)² : (- x²y⁵) = – x²y⁵

Thay x = 1/2 và y = – 1 vào biểu thức ta được:

-(1/2 )².(-1)5 = -1/4 .(-1) = 1/4

Bài 10:

Tính giá trị của biểu thức 15x⁴y³z² : 5xy²z² với x = 2, y = -10, z = 2004

hướng dẫn giải:

15x⁴y³z² : 5xy²z² với x = 2, y = -10, z = 200

Ta có 15x⁴y³z² : 5xy²z² = 3 . x⁴ – 1 . y³ – 2 . z² – 2 = 3x³y

Tại x = 2, y = -10, z = 2004

Ta được: 3 . 2³(-10) = 3 . 8 . (-10) = -240.

Bài 11: Làm tính chia:

a, x²yz : xyz

b, x³y⁴ : x³y

Lời giải:

a, x²yz : xyz = (x² : x)(y : y)(z : z) = x

b, x³y⁴ : x³y = (x³ : x³)(y⁴ : y) = y³

Bài 12: Làm tính chia:

a, (x + y)² : (x + y)

b, (x – y)⁵ : (y – x)⁴

c, (x – y + z)⁴ : (x – y + z)³

Lời giải:

a, (x + y)² : (x + y) = x + y

b, (x – y)⁵ : (y – x)⁴ = (x – y)⁵ : (x – y)⁴ = x – y

c, (x – y + z)⁴ : (x – y + z)³ = (x – y + z)

Vậy là các bạn vừa được tìm hiểu về chuyên đề chia đơn thức cho đơn thức toán 8. Hi vọng các bạn đã dược ôn lại quy tắc chia đơn thức cho đơn thức và các dạng toán thường gặp. Hẹn gặp lại các bạn trong những bài viết sau nhé ! Xem thêm 7 hằng đáng thức đáng nhớ tại đường link này em nhé !

Bản quyền bài viết thuộc Trường Trung Cấp Nghề Thương Mại Du Lịch Thanh Hoá. Mọi hành vi sao chép đều là gian lận!
Nguồn chia sẻ: https://tmdl.edu.vn/chia-don-thuc-cho-don-thuc-lop-8-ly-thuyet-va-cac-dang-toan/

Trang chủ: tmdl.edu.vn
Danh mục bài: Giáo dục