Các phép biến đổi biểu thức chứa căn thức bậc hai cần ghi nhớ
Lý thuyết về phương trình chứa căn thức bậc hai học sinh đã đươc tìm hiểu trong chương trình Toán 9, phân môn Đại số. Nhằm giúp các bạn nắm hơn các phép biến đổi biểu thức chứa căn thức bậc hai cùng nhiều dạng toán thường gặp, Trường Trung Cấp Nghề Thương Mại Du Lịch Thanh Hoá đã chia sẻ bài viết sau đây. Bạn tìm hiểu nhé !
I. PHƯƠNG TRÌNH CHỨA CĂN THỨC BẬC HAI LÀ GÌ?
Bạn đang xem bài: Các phép biến đổi biểu thức chứa căn thức bậc hai cần ghi nhớ
Phương trình chứa căn thức bậc hai là phương trình có chứa ẩn số dưới dấu căn bậc hai.
II. CÁC PHÉP BIẾN ĐỔI BIỂU THỨC CHỨA CĂN THỨC BẬC HAI
a) Đưa một thừa số ra ngoài dấu căn
Với hai biểu thức A, B mà B ≥ 0 ta có
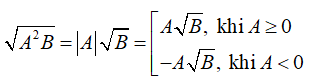
Ví dụ:
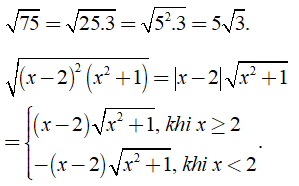
b) Đưa thừa số vào trong dấu căn
Với A ≥ 0, B ≥ 0 thì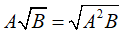 
Với A < 0, B ≥ 0 thì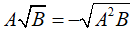 
Ví dụ:
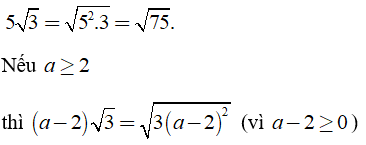
c) Khử mẫu của biểu thức dưới dấu căn.
Với AB ≥ 0 và B ≠ 0 thì
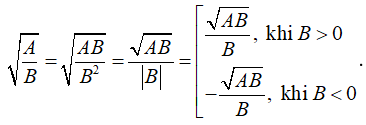
Ví dụ: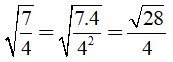 
d) Trục căn thức ở mẫu
Trục căn thức ở mẫu số là biến đổi để biểu thức đó mất căn thức ở mẫu số
• Với các biểu thức A, B mà B > 0 ta có: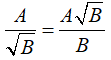 
Ví dụ:
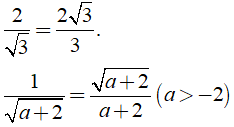
• Với các biểu thức A, B, C mà A ≥ 0, A ≠ B2, ta có:
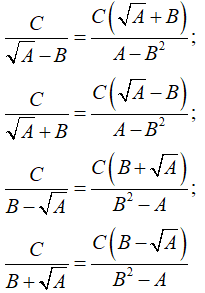
Ví dụ:
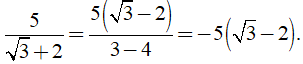
• Với các biểu thức A, B, C mà A ≥ 0, B ≥ 0, A ≠ B ta có:
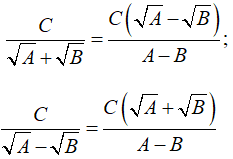
Ví dụ:
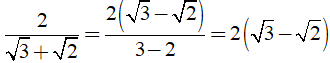
III. BÀI TẬP BIẾN ĐỔI BIỂU THỨC CHỨA CĂN THỨC BẬC HAI
Bài 1:
Đưa thừa số vào trong dấu căn:
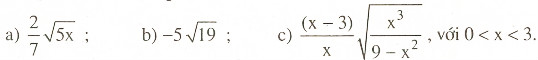
Giải:
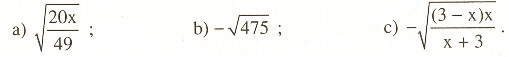
Bài 2:
Đưa thừa số ra ngoài dấu căn:
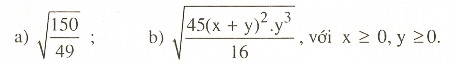
Giải:
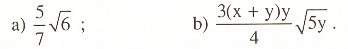
Bài 3:
Đưa thừa số ra ngoài dấu căn:
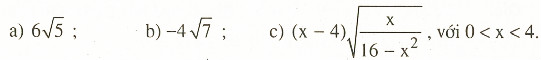
Giải:
Bài 4:
Rút gọn biểu thức:
Giải:
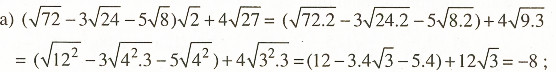
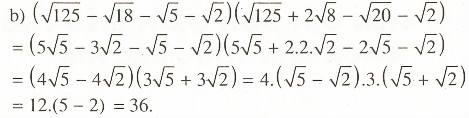
Bài 5:
So sánh:
Giải:
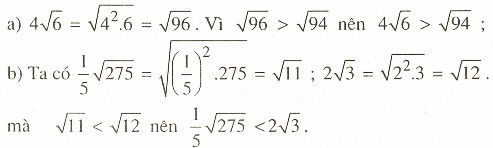
Bài 6:
Giải phương trình:
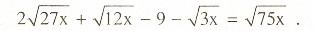
Giải:
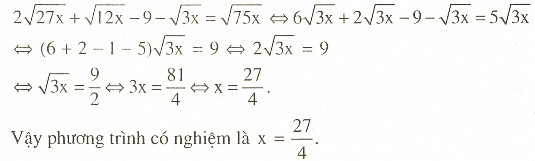
Bài 7:
Đưa thừa số ra ngoài dấu căn:
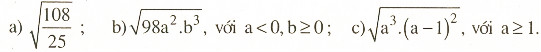
Giải
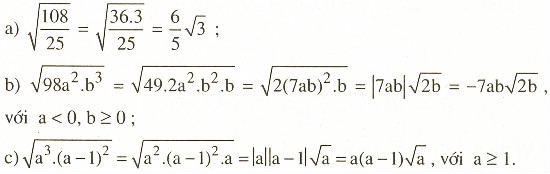
Bài 8:
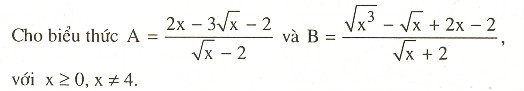
a) Rút gọn biểu thức A, B.
b) Tính giá trị của x để A – B = 2.
Giải:
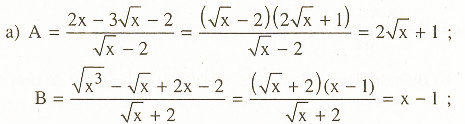
b) A – B = 2 <=> 2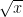
– x = 0 <=> x = 0 hoặc x = 4, nhưng x = 4 không thỏa mãn điều kiện. Vậy giá trị cần tìm là x = 0.
Bài 9:
Cho biểu thức :
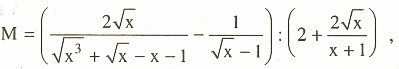
a) Rút gọn biểu thức M.
b) Tìm giá trị của x để M ≤ 0.
Giải:
Bài 10:
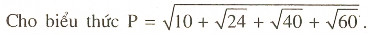
Hãy biểu diễn P dưới dạng tổng ba căn bậc hai.
Giải:
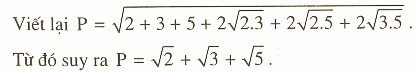
Vậy là các bạn vừa được tìm hiểu các phép biến đổi biểu thức chứa căn thức bậc hai cùng nhiều dạng toán thường gặp. Hi vọng, chia sẻ cùng bài viết bạn đã nắm vững hơn phần kiến thức Đại số 9 tối quan trọng này. Hẹn gặp lại các bạn trong những bài viết sau
Bản quyền bài viết thuộc Trường Trung Cấp Nghề Thương Mại Du Lịch Thanh Hoá. Mọi hành vi sao chép đều là gian lận!
Nguồn chia sẻ: https://tmdl.edu.vn/cac-phep-bien-doi-bieu-thuc-chua-can-thuc-bac-hai-can-ghi-nho/
Trang chủ: tmdl.edu.vn
Danh mục bài: Giáo dục
