Công thức Bayes

Công thức xác suất đầy đủ, công thức Bayes

1) Công thức xác suất đầy đủ

a) Hệ đầy đủ các biến cố

Bạn đang xem bài: Công thức Bayes

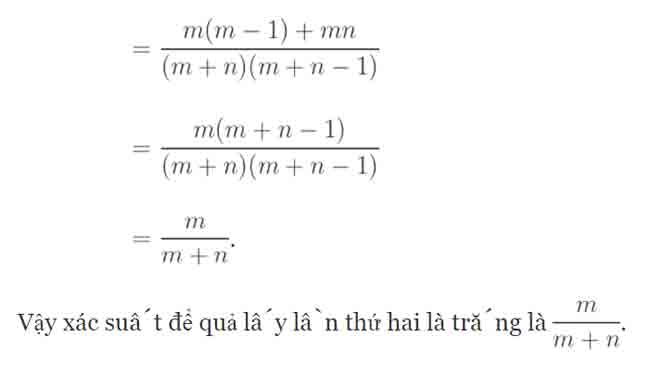
Ví dụ 3: 

Có 10 chiếc túi như sau:

4 túi loại 1, trong mỗi túi loại 1 chứa 6 viên bi trắng và 4 viên bi đen,

2 túi loại 2, trong mỗi túi loại 2 chứa 3 viên bi trắng và 7 viên bi đen,

1 túi loại 3, trong mỗi túi loại 3 chứa 7 viên bi trắng và 3 viên bi đen,

3 túi loại 4, trong mỗi túi loại 4 chứa 4 viên bi trắng và 6 viên bi đen.

Chọn ngẫu nhiên 1 chiếc túi rồi lấy ngẫu nhiên 2 viên bi. Tính xác suất để lấy được hai viên bi cùng màu.

Lời giải:  

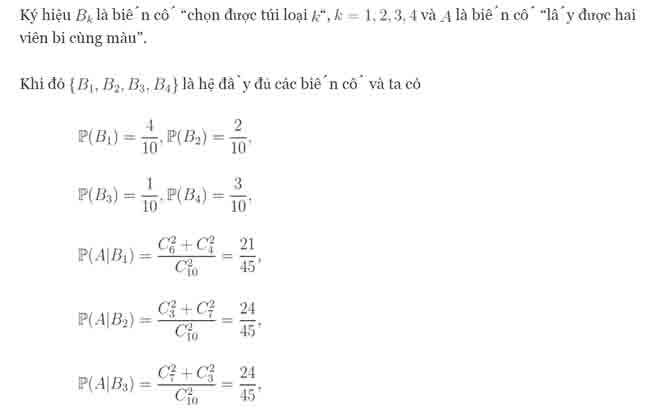
Ví dụ 4: 

Có hai cái hộp. Hộp thứ nhất có 4 bi trắng và 5 bi đen. Hộp thứ hai có 5 bi trắng và 4 bi đen. Chọn ngẫu nhiên 3 viên bi ở hộp thứ nhất bỏ vào hộp thứ hai rồi sau đó chọn ngẫu nhiên một viên bi ở hộp thứ hai ra. Tính xác suất để lấy được bi trắng từ hộp thứ hai.

Lời giải:

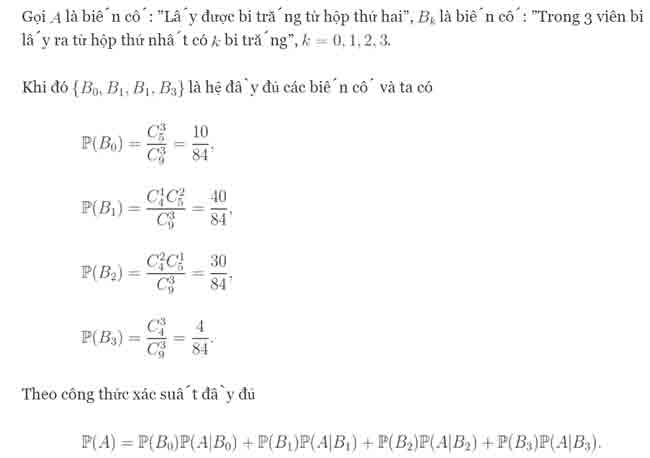
Ví dụ 5:

Trong một cái hộp có  sản phẩm, ta bỏ vào cái hộp đó một sản phẩm tốt sau đó lấy ngẫu nhiên ra một sản phẩm. Tính xác suất để sản phẩm lấy ra là tốt nếu mọi giả thiết về trạng thái cấu thành ban đầu của hộp là đồng xác suất.

Lời giải:

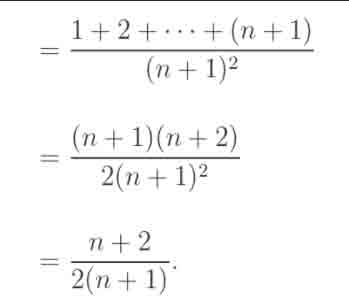
Công thức Bayes

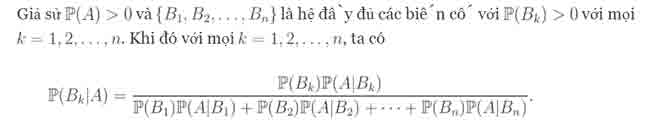
Ví dụ 6:

Dây chuyền lắp ráp nhận được các chi tiết do hai máy sản xuất. Trung bình máy thứ nhất cung cấp 60% chi tiết, máy thứ hai cung cấp 40% chi tiết. Khoảng 90% chi tiết do máy thứ nhất sản xuất là đạt tiêu chuẩn, còn 85% chi tiết do máy thứ hai sản xuất là đạt tiêu chuẩn. Lấy ngẫu nhiên từ dây chuyền một sản phẩm, thấy nó đạt tiêu chuẩn. Tìm xác suất để sản phẩm đó do máy thứ nhất sản xuất.

Lời giải:

Công thức Bayes – Định lý Bayes

Ví dụ 1. Dây chuyền lắp ráp nhận được các chi tiết do hai máy sản xuất. Trung bình máy thứ nhất cung cấp 60% chi tiết, máy thứ hai cung cấp 40% chi tiết. Khoảng 90% chi tiết do máy thứ nhất sản xuất là đạt tiêu chuẩn, còn 85% chi tiết do máy thứ hai sản xuất là đạt tiêu chuẩn. Lấy ngẫu nhiên từ dây chuyền một sản phẩm, thấy nó đạt tiêu chuẩn. Tìm xác suất để sản phẩm đó do máy thứ nhất sản xuất.

Hướng dẫn. Gọi A là biến cố: “Chi tiết lấy từ dây chuyền đạt tiêu chuẩn”, B1 là biến cố: “Chi tiết do máy thứ nhất sản xuất” và B2 là biến cố: “Chi tiết do máy thứ hai sản xuất”. Ta cần tính xác suất P(B1|A).

Theo công thức Bayes

Sau đây là một bài toán khá nổi tiếng trong xác suất thống kê, được giải theo nhiều cách khác nhau. Ta hãy thử giải bài toán này bằng định lý Bayes.
Ví dụ 2.[Bài toán Tuesday Child] Một gia đình có hai đứa trẻ. Biết có ít nhất có một đứa trẻ là con gái và sinh vào thứ 3. Hỏi xác suất 2 đứa trẻ đều là con gái là bao nhiêu?

Hướng dẫn. Chúng ta có nhận xét sau:

• Xác suất để một đứa trẻ sinh vào một ngày nhất định trong tuần là 1/7.
• Giới tính của đứa trẻ và ngày sinh của nó là 2 sự kiện không liên quan đến nhau.

Ta ký hiệu các biến cố như sau:

• B là biến cố “Ít nhất 1 đứa trẻ là con gái sinh ra vào thứ 3”,
• A là biến cố “Cả 2 đứa trẻ đều là con gái”, xác suất là P(A)=1/4,
• A1 là biến cố “Chỉ một trong 2 đứa trẻ là con gái”, P(A1)=1/2,
• C là biến cố “Đứa trẻ sinh ra vào thứ 3”, P(C)=1/7,

P(B) là xác suất sự ít nhất 1 đứa trẻ là con gái sinh ra vào thứ 3. Sự kiện này bao gồm 2 khả năng:

• Cả 2 đứa trẻ đều là con gái A,
• Chỉ 1 đứa trẻ là con gái A1.

Ta có

Chúng ta có thể minh họa bằng hình vẽ sau đây, xác suất cần tìm chính bằng số ô màu xanh chia cho tổng số ô màu vàng và xanh.

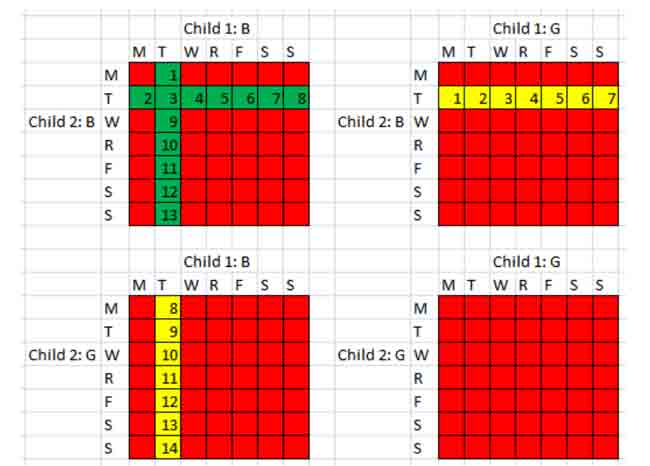
Ta dùng một đoạn code Python nho nhỏ để kiểm tra thử kết quả vừa tính được.

import random
def random_kid():
gender = random.choice(["boy", "girl"])
birth_date = random.choice(["mon", "tue", "wed", "thu", "fri", "sat", "sun"])
return (gender, birth_date)
both_girls = 0
tuesday_girl = 0
random.seed(0)
total = 100000
for _ in range(total):
first_child = random_kid()
second_child = random_kid()
if first_child == ("girl", "tue") or second_child == ("girl", "tue"):
tuesday_girl += 1
if first_child[0] == "girl" and second_child[0] == "girl":
both_girls += 1
print("both_girls = ", both_girls)
print("tuesday_girl = ", tuesday_girl)
print("P(both_girls|tuesday_girl) = ", both_girls / tuesday_girl)

Đoạn code trên thực hiện random 100K dữ liệu. Thu được kết quả in ra như sau

both_girls = 6506
tuesday_girl = 13637
P(both_girls|tuesday_girl) = 0.4770844027278727

Xác suất tính ra tương đối sát với con số ta tính bằng định lý Bayes ở trên.

Giáo trình

Trang chủ: tmdl.edu.vn
Danh mục bài: Giáo dục