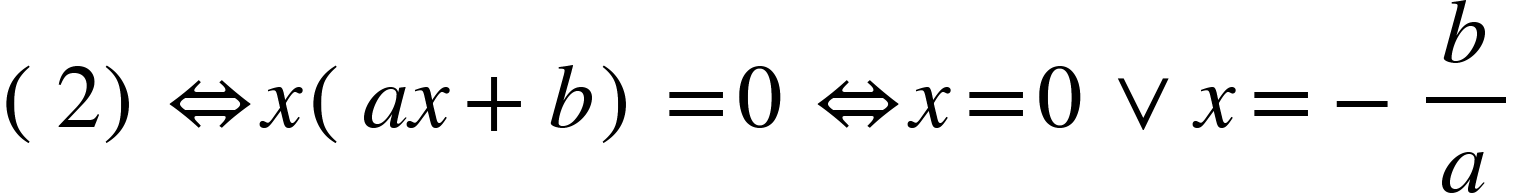Phương trình bậc 2 là gì?
Phương trình bậc 2 là phương trình có dạng ax2+bx+c=0 (a≠0) (1).
Giải phương trình bậc 2 là đi tìm các giá trị của x sao cho khi thay x vào phương trình (1) thì thỏa mãn ax2+bx+c=0
Bạn đang xem bài: Cách giải phương trình bậc 2
Giải phương trình bậc 2

Bước 1: Tính Δ=b2-4ac
Bước 2: So sánh Δ với 0
- Δ phương trình (1) vô nghiệm
- Δ = 0 => phương trình (1) có nghiệm kép
- Δ > 0 => phương trình (1) có 2 nghiệm phân biệt, ta dùng công thức nghiệm sau:
và
Mẹo nhẩm nghiệm phương trình bậc 2 nhanh:
- Nếu a+b+c=0 thì x1 = 1, x2 = c/a
- Nếu a-b+c=0 thì x1 = -1, x2 = -c/a

Ví dụ giải phương trình bậc hai
Giải phương trình 4x2 – 2x – 6 = 0 (2)
Δ=(-2)2 – 4.4.(-6) = 4 + 96 = 100 > 0 => phương trình (2) đã cho có 2 nghiệm phân biệt.
và
Bạn cũng có thể nhẩm theo cách nhẩm nghiệm nhanh, vì nhận thấy 4-(-2)+6=0, nên x1 = -1, x2 = -c/a = -(-6)/4=3/2. Nghiệm vẫn giống ở trên.
Giải phương trình 2x2 – 7x + 3 = 0 (3)
Tính Δ = (-7)2 – 4.2.3 = 49 – 24= 25 > 0 => (3) có 2 nghiệm phân biệt:
và
Để kiểm tra xem bạn đã tính nghiệm đúng chưa rất dễ, chỉ cần thay lần lượt x1, x2 vào phương trình 3, nếu ra kết quả bằng 0 là chuẩn. Ví dụ thay x1, 2.32-7.3+3=0.
Giải phương trình 3x2 + 2x + 5 = 0 (4)
Tính Δ = 22 – 4.3.5 = -56 phương trình (4) vô nghiệm.
Giải phương trình x2 – 4x +4 = 0 (5)
Tính Δ = (-4)2 – 4.4.1 = 0 => phương trình (5) có nghiệm kép:
Thực ra nếu nhanh ý, bạn cũng có thể nhìn ra đây chính là hằng đẳng thức đáng nhớ (a-b)2 = a2 – 2ab + b2 nên dễ dàng viết lại (5) thành (x-2)2 = 0 x=2.
Phân tích thành nhân tử
Nếu phương trình (1) có 2 nghiệm phân biệt x1, x2, lúc nào bạn cũng có thể viết nó về dạng sau: ax2 + bx + c = a(x-x1)(x-x2) = 0.
Trở lại với phương trình (2), sau khi tìm ra 2 nghiệm x1, x2 bạn có thể viết nó về dạng: 4(x-3/2)(x+1)=0.
Đi liền với phương trình bậc 2 còn có định lý Vi-et với rất nhiều ứng dụng như tính nhẩm nghiệm phương trình bậc 2 đã nói ở trên, tìm 2 số khi biết tổng và tích, xác định dấu của các nghiệm, hay phân tích thành nhân tử. Đây đều là những kiến thức cần thiết sẽ gắn liền với bạn trong quá trình học đại số, hay các bài tập giải và biện luận phương trình bậc 2 sau này, nên cần ghi nhớ kỹ và thực hành cho nhuần nhuyễn.
Phương trình bậc 2 một ẩn
Cho phương trình sau: ax2+bx+c=0 (a≠0), được gọi là phương trình bậc 2 với ẩn là x.
Công thức nghiệm: Ta gọi Δ=b2-4ac.Khi đó:
- Δ>0: phương trình tồn tại 2 nghiệm:.

- Δ=0, phương trình có nghiệm kép x=-b/2a
- Δ
Trong trường hợp b=2b’, để đơn giản ta có thể tính Δ’=b’2-ac, tương tự như trên:
- Δ’>0: phương trình có 2 nghiệm phân biệt.

- Δ’=0: phương trình có nghiệm kép x=-b’/a
- Δ’
Định lý Viet và ứng dụng trong phương trình bậc 2 một ẩn
Cho phương trình bậc 2 một ẩn: ax2+bx+c=0 (a≠0). Giả sử phương trình có 2 nghiệm x1 và x2, lúc này hệ thức sau được thỏa mãn:
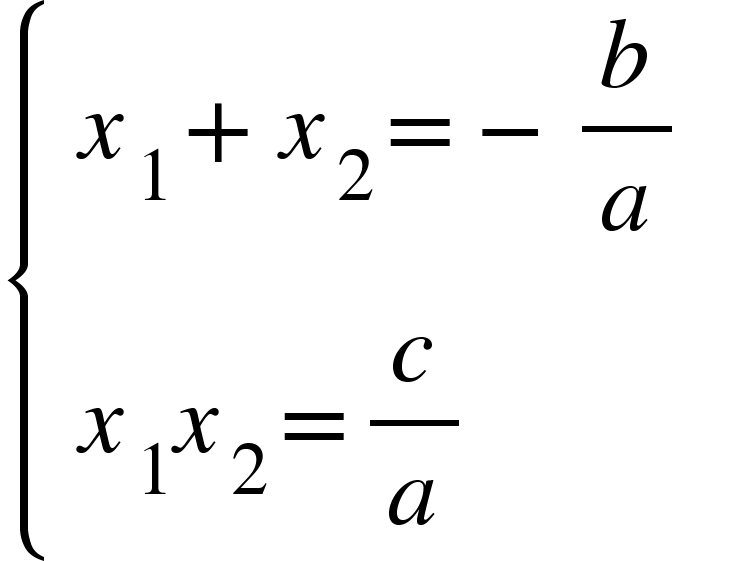
Dựa vào hệ thức vừa nêu, ta có thể sử dụng định lý Viet để tính các biểu thức đối xứng chứa x1 và x2
- x1+x2=-b/a
- x12+x22=(x1+x2)2-2x1x2=(b2-2ac)/a2
- …
Nhận xét: Đối với dạng này, ta cần biến đổi biểu thức làm sao cho xuất hiện (x1+x2) và x1x2 để áp dụng hệ thức Viet.
Định lý Viet đảo
Giả sử tồn tại hai số thực x1 và x2 thỏa mãn: x1+x2=S, x1x2=P thì x1 và x2 là 2 nghiệm của phương trình x2-Sx+P=0
Một số ứng dụng thường gặp của định lý Viet trong giải bài tập toán
- Nhẩm nghiệm phương trình bậc 2: cho phương trình ax2+bx+c=0 (a≠0),
- Nếu a+b+c=0 thì phương trình có nghiệm x1=1 và x2=c/a
- Nếu a-b+c=0 thì phương trình có nghiệm x1=-1 và x2=-c/a
- Phân tích đa thức thành nhân tử: cho đa thức P(x)=ax2+bx+c nếu x1 và x2 là nghiệm của phương trình P(x)=0 thì đa thức P(x)=a(x-x1)(x-x2)
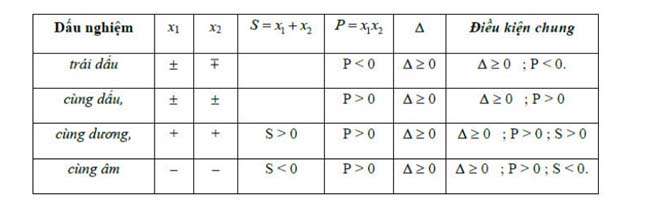
- Xác định dấu của các nghiệm: cho phương trình ax2+bx+c=0 (a≠0), giả sử x1 và x2 là 2 nghiệm của phương trình. Theo định lý Viet, ta có:
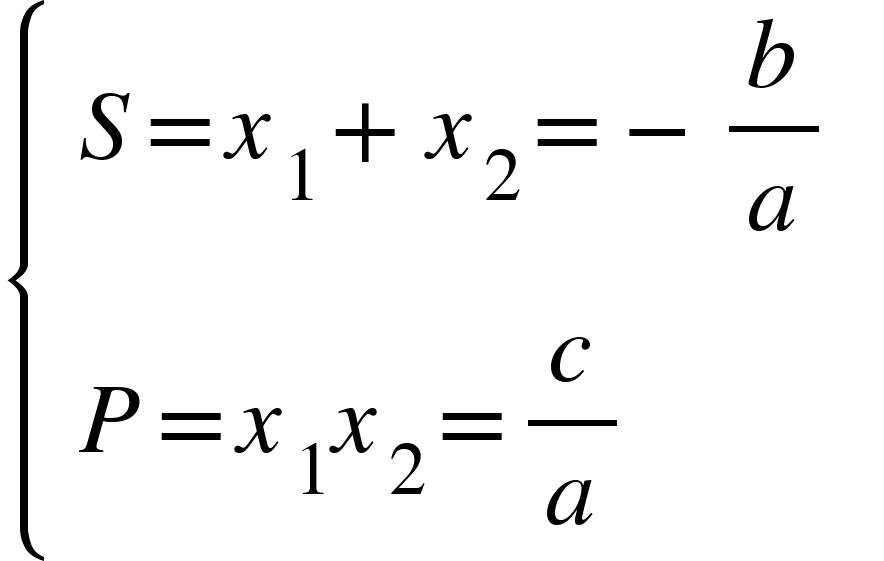
- Nếu S2 trái dấu.
- Nếu S>0, x1 và x2 cùng dấu:
- P>0, hai nghiệm cùng dương.
- P
Dạng bài tập về phương trình bậc 2 một ẩn
Dạng 1: Bài tập phương trình bậc 2 một ẩn không xuất hiện tham số
Để giải các phương trình bậc 2, cách phổ biến nhất là sử dụng công thức tính Δ hoặc Δ’, rồi áp dụng các điều kiện và công thức của nghiệm đã được nêu ở mục I.
Ví dụ 1: Giải các phương trình sau:
- x2-3x+2=0
- x2+x-6=0
Hướng dẫn:
- Δ=(-3)2-4.2=1. Vậy
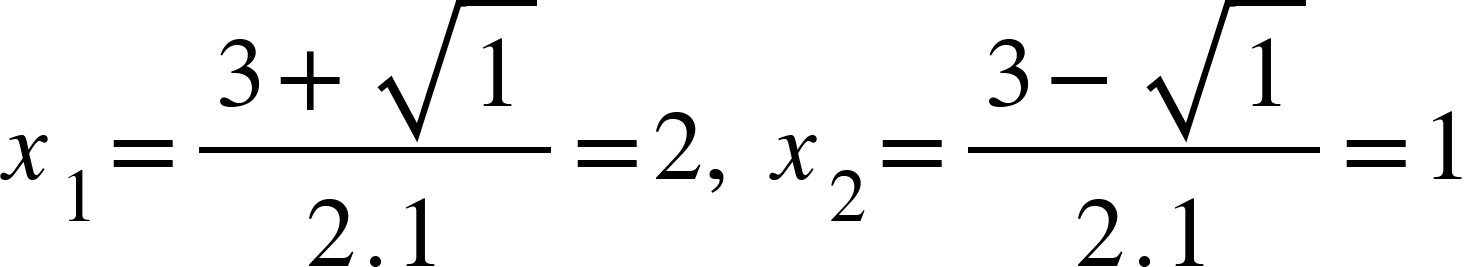
Ngoài ra, ta có thể áp dụng cách tính nhanh: để ý 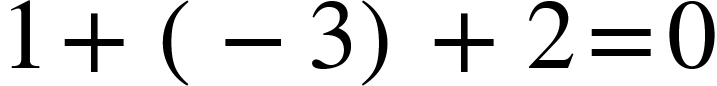
suy ra phương trình có nghiệm là x1=1 và x2=2/1=2
- Δ=12-4.(-6)=25. Vậy
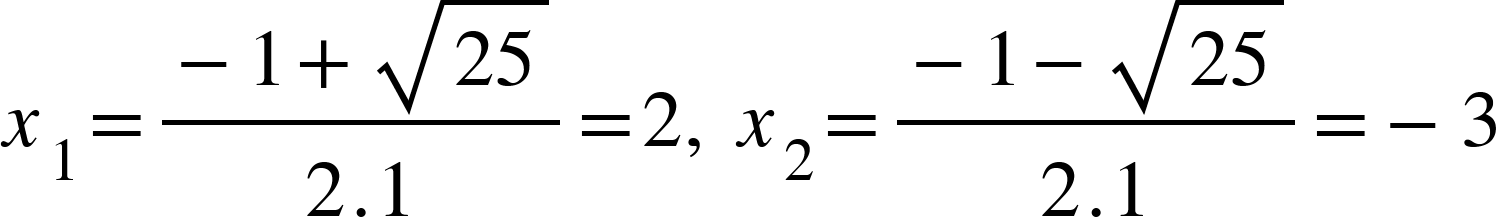
Tuy nhiên, ngoài các phương trình bậc 2 đầy đủ, ta cũng xét những trường hợp đặc biệt sau:
Phương trình khuyết hạng tử.
Khuyết hạng tử bậc nhất: ax2+c=0 (1).
Phương pháp:
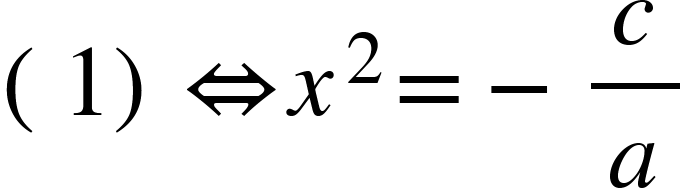
- Nếu -c/a>0, nghiệm là:

- Nếu -c/a=0, nghiệm x=0
- Nếu -c/a
Khuyết hạng tử tự do: ax2+bx=0 (2). Phương pháp:
Ví dụ 2: Giải phương trình:
- x2-4=0
- x2-3x=0
Hướng dẫn:
- x2-4=0 ⇔ x2=4 ⇔ x=2 hoặc x=-2
- x2-3x=0 ⇔ x(x-3)=0 ⇔ x=0 hoặc x=3
Phương trình đưa về dạng bậc 2.
Phương trình trùng phương: ax4+bx2+c=0 (a≠0):
- Đặt t=x2 (t≥0).
- Phương trình đã cho về dạng: at2+bt+c=0
- Giải như phương trình bậc 2 bình thường, chú ý điều kiện t≥0
Phương trình chứa ẩn ở mẫu:
- Tìm điều kiện xác định của phương trình (điều kiện để mẫu số khác 0).
- Quy đồng khử mẫu.
- Giải phương trình vừa nhận được, chú ý so sánh với điều kiện ban đầu.
Chú ý: phương pháp đặt t=x2 (t≥0) được gọi là phương pháp đặt ẩn phụ. Ngoài đặt ẩn phụ như trên, đối với một số bài toán, cần khéo léo lựa chọn sao cho ẩn phụ là tốt nhất nhằm đưa bài toán từ bậc cao về dạng bậc 2 quen thuộc. Ví dụ, có thể đặt t=x+1, t=x2+x, t=x2-1…
Ví dụ 3: Giải các phương trình sau:
- 4x4-3x2-1=0

Hướng dẫn:
- Đặt t=x2 (t≥0), lúc này phương trình trở thành:
4t2-3t-1=0, suy ra t=1 hoặc t=-¼
- t=1 ⇔ x2=1 ⇔ x=1 hoặc x=-1.
- t=-¼ , loại do điều kiện t≥0
Vậy phương trình có nghiệm x=1 hoặc x=-1.
- Ta có:

Dạng 2: Phương trình bậc 2 một ẩn có tham số
Biện luận số nghiệm của phương trình bậc 2.
Phương pháp: Sử dụng công thức tính Δ, dựa vào dấu của Δ để biện luận phương trình có 2 nghiệm phân biệt, có nghiệm kép hay là vô nghiệm.
Ví dụ 4: Giải và biện luận theo tham số m: mx2-5x-m-5=0 (*)
Hướng dẫn:
Xét m=0, khi đó (*) ⇔ -5x-5=0 ⇔ x=-1
Xét m≠0, khi đó (*) là phương trình bậc 2 theo ẩn x.

- Vì Δ≥0 nên phương trình luôn có nghiệm:
- Δ=0 ⇔ m=-5/2, phương trình có nghiệm duy nhất.
- Δ>0 ⇔ m≠-5/2, phương trình có 2 nghiệm phân biệt:
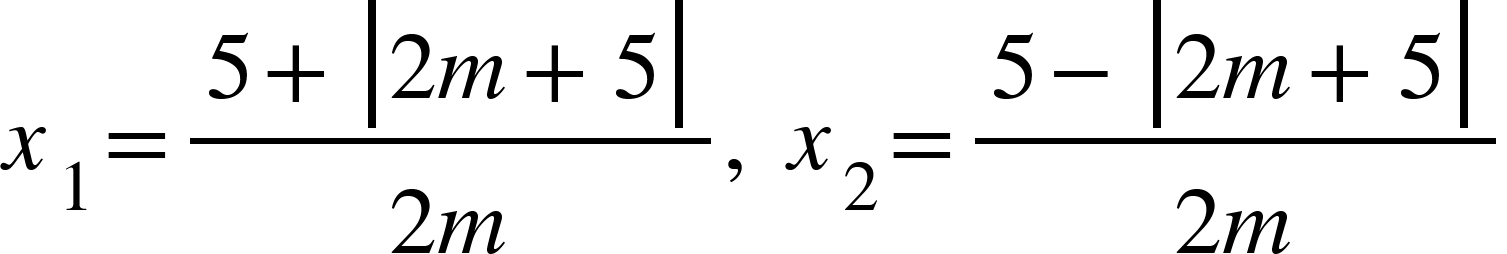
Xác định điều kiện tham số để nghiệm thỏa yêu cầu đề bài.
Phương pháp: để nghiệm thỏa yêu cầu đề bài, trước tiên phương trình bậc 2 phải có nghiệm. Vì vậy, ta thực hiện theo các bước sau:
- Tính Δ, tìm điều kiện để Δ không âm.
- Dựa vào định lý Viet, ta có được các hệ thức giữa tích và tổng, từ đó biện luận theo yêu cầu đề.
Ví dụ 5: Cho phương trình x2+mx+m+3=0 (*). Tìm m để phương trình (*) có 2 nghiệm thỏa mãn:

Hướng dẫn:
Để phương trình (*) có nghiệm thì:

Khi đó, gọi x1 và x2 là 2 nghiệm, theo định lý Viet:
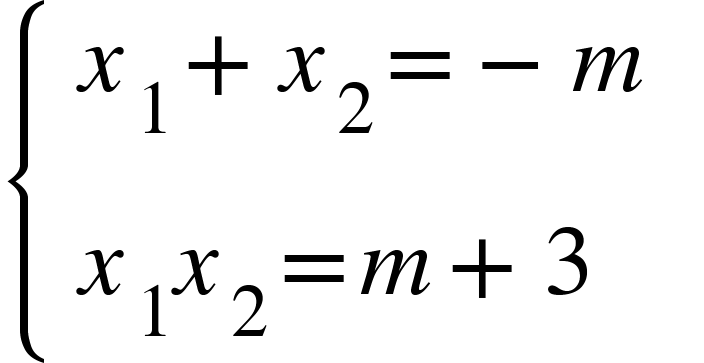
Mặt khác:

Theo đề:
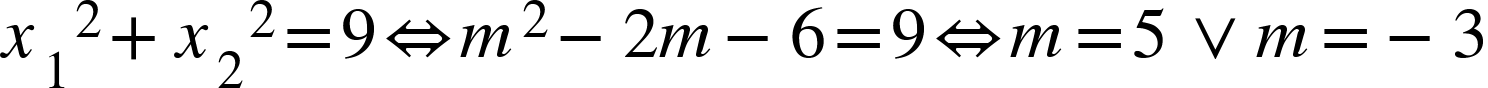
Thử lại:
- Khi m=5, Δ=-7
- Khi m=-3, Δ=9 >0 (nhận)
vậy m = -3 thỏa yêu cầu đề bài.





Lịch sử
Ngay từ năm 2000 trước Công Nguyên, các nhà toán học Babylon đã có thể giải những bài toán liên quan đến diện tích và các cạnh của hình chữ nhật. Có bằng chứng chỉ ra thuật toán này xuất hiện từ triều đại Ur thứ ba. Theo ký hiệu hiện đại, các bài toán này thường liên quan đến việc giải hệ gồm hai phương trình:{displaystyle x+y=p, xy=q}
tương đương với phương trình:
Các bước giải được người Babylon đưa ra như sau:
- Tính p/2.
- Bình phương kết quả tìm được.
- Trừ đi q.
- Tính căn bậc hai bằng bảng căn bậc hai.
- Cộng kết quả của bước (1) và (4) để tìm x. Điều này về cơ bản là tương đương với việc tính
Ở Babylon, Ai Cập, Hy Lạp, Trung Quốc, và Ấn Độ, phương pháp hình học được sử dụng để giải phương trình bậc hai. Tài liệu Berlin Papyrus của người Ai Cập có từ thời Trung vương quốc (từ năm 2050 đến 1650 trước CN) có chứa lời giải của phương trình bậc hai hai số hạng.[14] Trong nguyên bản kinh Sulba Sutras, khoảng thế kỷ 8 trước CN, phương trình bậc hai dạng ax2 = c và ax2 + bx = c được khảo sát bằng phương pháp hình học. Các nhà toán học Babylon từ khoản năm 400 trước CN và các nhà toán học Trung Quốc từ khoảng năm 200 trước CN đã sử dụng phương pháp phân chia hình học để giải các phương trình bậc hai với nghiệm dương.[15][16] Cuốn Cửu chương toán thuật của người Trung Quốc có ghi những quy tắc của phương trình bậc hai.[16][17] Trong những phương pháp hình học thuở đầu này không xuất hiện một công thức tổng quát. Tới khoảng năm 300 trước CN, nhà toán học Hy Lạp Euclid đã cho ra một phương pháp hình học trừu tượng hơn. Với cách tiếp cận hoàn toàn bằng hình học, Pythagoras và Euclid đã tạo dựng một phương pháp tổng quan để tìm nghiệm của phương trình bậc hai. Trong tác phẩm Arithmetica của mình, nhà toán học Hy Lạp Diophantus đã giải phương trình bậc hai, tuy nhiên chỉ cho ra một nghiệm, kể cả khi cả hai nghiệm đều là dương.[18]
Vào năm 628 CN, Brahmagupta, một nhà toán học Ấn Độ đưa ra lời giải rõ ràng đầu tiên (dù vẫn chưa hoàn toàn tổng quát) cho phương trình bậc hai ax2 + bx = c như sau: “Nhân số tuyệt đối (c) với bốn lần hệ số bình phương, cộng với bình phương hệ số số hạng ở giữa; căn bậc hai toàn bộ, trừ đi hệ số số hạng ở giữa, rồi chia cho hai lần hệ số bình phương là giá trị.” (Brahmasphutasiddhanta, Colebrook translation, 1817, tr 346)[13]:87 Điều này tương đương:
Thủ bản Bakhshali ra đời ở Ấn Độ vào thế kỷ 7 CN có chứa một công thức đại số cho việc giải phương trình bậc hai, cũng như những phương trình vô định. Muhammad ibn Musa al-Khwarizmi đi xa hơn trong việc cung cấp một lời giải đầy đủ cho phương trình bậc hai dạng tổng quát,[19] ông cũng đã mô tả phương pháp phần bù bình phương và thừa nhận rằng biệt thức phải dương,[19][20]:230 điều đã được ‘Abd al-Hamīd ibn Turk (Trung Á, thế kỷ 9) chứng minh. Turk là người đưa ra những biểu đồ hình học chứng minh rằng nếu biệt thức âm thì phương trình bậc hai vô nghiệm.[20]:234 Trong khi bản thân al-Khwarizmi không chấp nhận nghiệm âm, các nhà toán học Hồi giáo kế tục ông sau này đã chấp nhận nghiệm âm cũng như nghiệm vô tỉ.[19]:191[21] Cá biệt Abū Kāmil Shujā ibn Aslam (Ai Cập, thế kỷ 10) là người đầu tiên chấp nhận các số vô tỉ (thường ở dạng căn bậc hai, căn bậc ba hay căn bậc bốn) là nghiệm hay là hệ số của phương trình bậc hai.[22] Nhà toán học Ấn Độ thế kỷ thứ 9 Sridhara đã viết ra các quy tắc giải phương trình bậc hai.[23]
Nhà toán học người Do Thái Abraham bar Hiyya Ha-Nasi (thế kỷ 12, Tây Ban Nha) là tác giả cuốn sách đầu tiên của người châu Âu có chứa lời giải đầy đủ cho phương trình bậc hai dạng tổng quát.[24] Giải pháp của Ha-Nasi dựa nhiều vào tác phẩm của Al-Khwarizmi.[19] Lần đầu tiên hệ số âm của ‘x’ xuất hiện trong tác phẩm của nhà toán học người Trung Quốc Yang Hui (1238–1298 CN), dù vậy ông cho điều này là từ nhà toán học Liu Yi ở thời trước đó.[25] Vào năm 1545 Gerolamo Cardano biên soạn các tác phẩm liên quan đến phương trình bậc hai. Công thức nghiệm cho mọi trường hợp lần đầu đạt được bởi Simon Stevin vào năm 1594.[26] Năm 1637 René Descartes công bố tác phẩm La Géométrie trong đó có chứa công thức nghiệm mà chúng ta biết ngày nay. Lời giải tổng quát xuất hiện lần đầu trong tài liệu toán học hiện đại vào năm 1896, bởi Henry Heaton.
Bản quyền bài viết thuộc Trường Trung Cấp Nghề Thương Mại Du Lịch Thanh Hoá. Mọi hành vi sao chép đều là gian lận!
Nguồn chia sẻ: https://tmdl.edu.vn https://tmdl.edu.vn/cach-giai-phuong-trinh-bac-2/
Trang chủ: tmdl.edu.vn
Danh mục bài: Giáo dục