Tìm hiểu các phương pháp xét dấu đạo hàm để tìm cực trị của hàm số

Tìm hiểu các phương pháp xét dấu đạo hàm để tìm cực trị của hàm số

Bài viết hôm nay, Trường Trung Cấp Nghề Thương Mại Du Lịch Thanh Hoá sẽ giới thiệu đến quý thầy cô và các bạn một số phương pháp xét dấu đạo hàm để tìm cực trị của hàm số cực hay cùng nhiều dạng bài tập thường gặp. Hãy dành thơi gian chia sẻ để có thêm nguồn tư liệu quý phục vụ quá trình dạy và học được tốt hơn các bạn nhé !

I. CỰC TRỊ CỦA HÀM SỐ LÀ GÌ?

Bạn đang xem bài: Tìm hiểu các phương pháp xét dấu đạo hàm để tìm cực trị của hàm số

1. Cực trị của hàm số là gì?

Cho hàm số y = f(x) liên tục trên khoảng (a; b) và điểm x0 ∈ (a; b).

• Nếu tồn tại số h > 0 sao cho f(x) < f(x0), ∀x ∈ (x0 – h ; x0 + h), x ≠ x0 thì ta nói hàm số f đạt cực đại tại x0 .
• Nếu tồn tại số h > 0 sao cho f(x) > f(x0), ∀x ∈ (x0 – h ; x0 + h), x ≠ x0 thì ta nói hàm số f đạt cực tiểu tại x0 .

Định lý 1: Cho hàm số y = f(x) liên tục trên khoảng K = (x0 – h ; x0 + h) (h > 0) và có đạo hàm trên K hoặc trên K ∖{ x0 }.

• Nếu {f′(x)>0∣∀(x0−h;x0)f′(x)<0∣∀(x0;x0+h) thì x0 là điểm cực đại của hàm số.
• Nếu {f′(x)>0∣∀(x0−h;x0)f′(x)<0∣∀(x0;x0+h) thì x0 là điểm cực tiểu của hàm số.

Định lý 2. Cho hàm số y = f(x) có đạo hàm cấp hai trên khoảng K = (x0 – h; x0 + h) (h > 0).

• Nếu f'(x0) = 0, f”(x0) > 0  thì x0 là điểm cực tiểu của hàm số f.
• Nếu f'(x0) = 0, f”(x0) < 0 thì x0 là điểm cực đại của hàm số f

II. PHƯƠNG PHÁP TÌM CỰC TRỊ CỦA HÀM SỐ CÓ ĐẠO HÀM

Công thức 1:

• Bước 1. Tìm tập xác định của hàm số.
• Bước 2. Tínhf'(x). Tìm các điểm tại đó f'(x)bằng 0 hoặc f'(x) không xác định.
• Bước 3. Lập bảng biến thiên.
• Bước 4. Từ bảng biến thiên suy ra các điểm cực trị.

Công thức 2:

• Bước 1. Tìm tập xác định của hàm số.
• Bước 2. Tính f'(x). Giải phương trình f'(x)và ký hiệux_i (i=1,2,3,…)là các nghiệm của nó.
• Bước 3. Tính f”(x) và f”(x_i ) .
• Bước 4. Dựa vào dấu của f”(x_i )suy ra tính chất cực trị của điểm x_i.

III. PHƯƠNG PHÁP XÉT DẤU ĐẠO HÀM ĐỂ TÌM CỰC TRỊ CỦA HÀM SỐ

Để xét dấu cho biểu thức g(x)=p(x)/q(x)ta làm như sau:

– Bước 1: Điều kiện: q(x)≠0

Tìm tất cả các nghiệm của p(x); q(x)và sắp xếp các nghiệm đó theo thứ tự tăng dần và điền vào trục số Ox.

– Bước 2: Cho x→+∞ để xác định dấu cùa g(x) khi x→+∞.

– Bước 3: Xác định dấu của các khoảng còn lại dựa vào quy tắc sau:

Chú ý: Qua nghiệm bội lẻ thì g(x) đổi dấu còn qua nghiệm bội chẵn thì g(x) không đổi dấu (chẵn giữ nguyên, lẻ đổi dấu).

Ví dụ minh họa:

a. Xét dấu của biểu thức f(x) = 2x(x+2)-(x+2)(x+1)

b. Lập bảng biến thiên và vẽ trong cùng một hệ tọa độ vuông góc đồ thị của các hàm số : y = 2x(x+2) ( C1 ) và y = (x+2)(x+1)(C2)

Tính tọa độ giao điểm A và B của (C1) và (C2).

c. Tính các hệ số a, b, c để hàm số y = ax² + bx + c có giá trị lớn nhất bằng 8 và độ thị của nó đi qua A và B.

a) f(x) = 2x.(x+2) – (x+2)(x+1) = 2×2 + 4x – (x2 + 3x + 2) = x2 + x – 2

Tam thức x2 + x – 2 có hai nghiệm x1 = -2 và x2 = 1, hệ số a = 1 > 0.

Vậy:

+ f(x) > 0 nếu x > x2 = 1 hoặc x < x1 = -2, hay x ∈ (-∞; -2) ∪ (1; + ∞)

+ f(x) < 0 nếu x1 < x < x2 hay x ∈ (-2; 1)

+ f(x) = 0 nếu x = -2 hoặc x = 1.

b)

* Hàm số y = 2x(x+2) = 2×2 + 4x có đồ thị (C1) là parabol có:

+ Tập xác định: D = R

+ Đỉnh I1( -1; -2)

+ Trục đối xứng: x = -1

+ Giao điểm với trục tung tại gốc tọa độ.

+ Giao điểm với trục hoành tại O(0; 0) và M(-2; 0).

+ Bảng biến thiên:

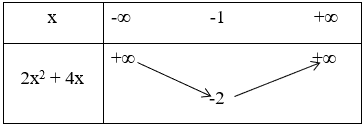
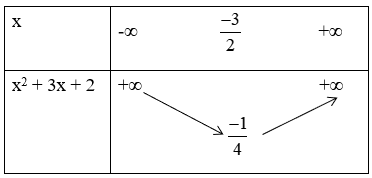
* Hàm số y = (x + 2)(x+1) = x2 + 3x + 2 có đồ thị (C2) là parabol có:

+ Tập xác định D = R.

+ Đỉnh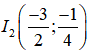 

+ Trục đối xứng: x = -3/2

+ Giao với trục tung tại D(0; 2)

+ Giao với trục hoành tại M(-2; 0) và E(-1; 0)

+ Bảng biến thiên

* Đồ thị:

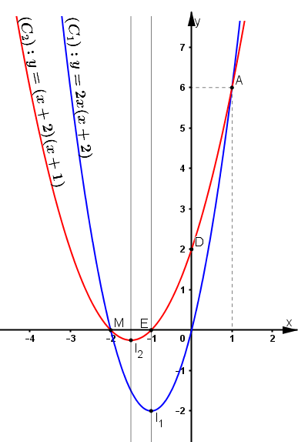
* Tìm tọa độ giao điểm:

Cách 1: Dựa vào đồ thị hàm số:

Nhìn vào đồ thị thấy (C1) cắt (C2) tại A(1; 6) và B ≡ M(-2; 0)

Cách 2: Tính:

Hoành độ giao điểm của (C1) và (C2) là nghiệm của phương trình:

2x(x + 2) = (x + 2)(x + 1)

⇔ (x + 2).2x – (x + 2)(x + 1) = 0

⇔ (x + 2).(2x – x – 1) = 0

⇔ (x + 2).(x – 1) = 0

⇔ x = -2 hoặc x = 1.

+ x = -2 ⇒ y = 0. Ta có giao điểm B(-2; 0)

+ x = 1 ⇒ y = 6. Ta có giao điểm A(1; 6).

c)

+ Đồ thị hàm số y = ax2 + bx + c đi qua điểm A(1; 6) và B(-2; 0)

⇔ tọa độ A và B thỏa mãn phương trình y = ax2 + bx + c

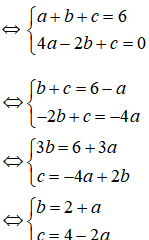
+ Ta có bảng biến thiên của hàm số y = ax2 + bx + c:

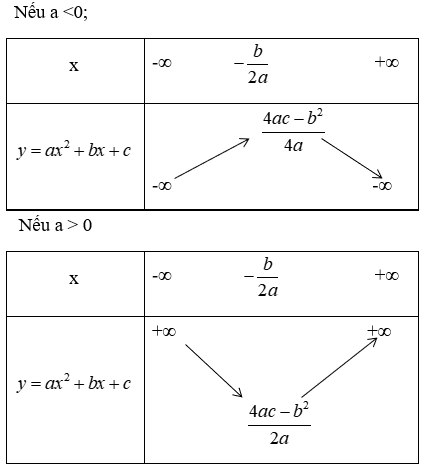
Nhận thấy y đạt giá trị lớn nhất bằng 8

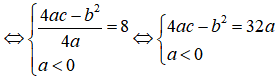
Thay b = 2 + a và c = 4 – 2a vào biểu thức 4ac – b2 = 32a ta được:

4.a.(4 – 2a) – (2 + a)2 = 32a

⇔ 16a – 8a2 – (a2 + 4a + 4) = 32a

⇔ 16a– 8a2 – a2 – 4a – 4 – 32a = 0

⇔ -9a2 – 20a – 4 = 0

⇔ a = -2 hoặc a = -2/9.

Nếu a = -2 ⇒ b = 0, c = 8, hàm số y = -2×2 + 8

Nếu a = -2/9 ⇒ b = 16/9, c = 40/9, hàm số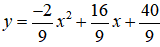 

IV. CÁC DẠNG BÀI TẬP VỀ ĐẠO HÀM

Bài 1: Tìm đạo hàm của các hàm số sau:

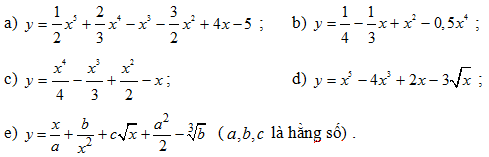
Đáp số:

a. 

b. 

c. y’ = x³ – x² + x – 1

Bài 2: Tìm đạo hàm của các hàm số sau:

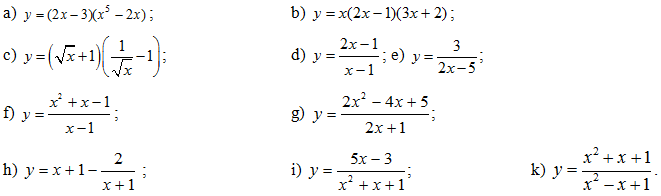
Đáp số:

a. y’ = 12x5 – 8x -15x4 + 6	b. y’ = 18x2 + 2x – 2
c.	d. y’ = -1/(x- 1)2
e. y’ = -6/(2x – 5)2	f. y’ = (x2 – 2x -1)/(x – 1)2
g. y’=(8x3 – 8x2 + 4x – 10)/(2x + 1)2	h. y’ = 1 + 2/(x + 1)2
i. y’ = (-5x2 + 6x + 8)/(x2 + x + 1)2	k. y’ = (-5x2 + 6x + 8)/(x2 – x + 1)2

Bài 3: Tìm đạo hàm của các hàm số sau:

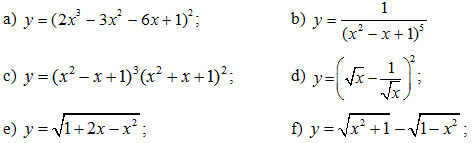
Bài 4: Cho hàm số . Xác định giá trị của tham số m để:

a. y’ ≤ 0, ∀ x∈ 

b. y’ = 0 có hai nghiệm phân biệt cùng âm.

c. y’ = 0 có hai nghiệm phân biệt thỏa mãn điều kiện x₁² + x₂² = 3.

Bài 5: Cho hàm số (C): y = mx⁴ + (m² – 9)x² + 10 (1) (m là tham số). Xác định giá trị của m để hàm số có y’ = 0 có 3 nghiệm phân biệt.

Bài 6: Cho hàm số (C): y = x² – 2x + 3. Viết phương trình tiếp tuyến với (C):

a. Tại điểm có hoành độ x₀ = 2

b. Biết tiếp tuyến song song với đường thẳng 4x – y = 9

c. Vuông góc với đường thẳng 2x + 4y – 2011 = 0

d. Biết tiếp tuyến đi qua điểm A(1; 0)

Bài 7: Cho hàm số:  (1).

a. Viết phương trình tiếp tuyến của (C) tại điểm M(-1;-1)

b. Viết phương trình tiếp tuyến của (C) tại giao điểm của (C) với trục hoành.

c. Viết phương trình tiếp tuyến của (C) tại giao điểm của (C) với trục tung.

d. Viết phương trình tiếp tuyến của (C) biết tiếp tuyến song song với đường thẳng (d): 4x – y + 1 = 0

e. Viết phương trình tiếp tuyến của (C) biết tiếp tuyến vuông góc với đường thẳng (d’): 4x + y – 8 = 0

Bài 8: Cho hàm số y = x³ – 3x² (C)

a. Viết phương trình tiếp tuyến của đồ thị (C) tại điểm I(1;-2)

b. Chứng minh rằng các tiếp tuyến khác của đồ thị (C) không đi qua I.

Bài 9: Cho hàm số:  (1). Tính diện tích tam giác tạo bởi các trục tọa độ và tiếp tuyến của đồ thị hàm sô (1) tại điểm M(-2; 5).

Bài 10: Cho hàm số (C): . Tìm điểm M thuộc (C), biết tiếp tuyến của (C) tại M cắt hai trục tọa độ tại A, B và tam giác OAB có diện tích bằng 2.

Bài 11:

a. Viết phương trình tiếp tuyến của đồ thị hàm số: y = x⁴ – 2x² + 5 tại điểm A(2;13).

b. Viết phương trình tiếp tuyến của đồ thị hàm số y = x³ – 3x² + 2 biết tiếp tuyến song song với d có phương trình y = -3x + 2

c. Viết phương trình tiếp tuyến của đồ thị hàm số y = x³ – 3x² + 2 biết tiếp tuyến song song với d có phương trình y = -3x + 2

d. Cho hàm số y = 3x³ + x² – 2 có đồ thị C. Phương trình tiếp tuyến của C tại điểm có hoành độ là nghiệm của phương trình y” = 0 là bao nhiêu?

e. Phương trình tiếp tuyến của đồ thị hàm số: y = x³ – 3x + 1 tại điểm có hoành độ = 1 có hệ số góc là k bằng bao nhiêu? Tìm điểm cực tiểu của hàm số: y = -x² + 2x – 1?

Vậy là các bạn vừa được tìm hiểu một số phương pháp xét dấu đạo hàm để tìm cực trị của hàm số và nhiều dạng bài tập liên quan. Hi vọng, đây sẽ là nguồn tư liệu thiết yếu phục vụ quá trình dạy và học được tốt hơn. Xem thêm công thức tính cực trị của hàm số tại đường link này nhé !

Bản quyền bài viết thuộc Trường Trung Cấp Nghề Thương Mại Du Lịch Thanh Hoá. Mọi hành vi sao chép đều là gian lận!
Nguồn chia sẻ: https://tmdl.edu.vn https://tmdl.edu.vn/tim-hieu-cac-phuong-phap-xet-dau-dao-ham-de-tim-cuc-tri-cua-ham-so/

Trang chủ: tmdl.edu.vn
Danh mục bài: Giáo dục