Các dạng toán tính tổng dãy số lũy thừa có quy luật là một trong những chuyên đề có khá nhiều bài tập được gọi là “khó nhằn” và gây ‘căng thẳng đầu óc’ cho các bạn học sinh lớp 6, đây có thể coi là dạng toán dành cho học sinh khá giỏi.
Vì vậy, nhằm giúp các em học sinh “giải tỏa được căng thẳng” khi gặp các dạng toán về tính tổng dãy số lũy thừa có quy luật, trong bài viết này chúng ta hãy cùng hệ thống lại một số dạng toán này cùng công thức và cách giải, sau đó vận dụng làm các bài tập.
Bạn đang xem bài: Các dạng toán Tính tổng Dãy số lũy thừa có quy luật và bài tập – Toán lớp 6
I. Dạng toán tính tổng dãy sử dụng phương pháp quy nạp.
– Đối với 1 số trường hợp khi tính tổng hữu hạn:
Sn = a1 + a2 + . . . + an (*)
khi mà ta có thể biết được kết quả (đề bài toán cho ta biết kết quả hoặc ta dự đoán được kết quả), thì ta sử dụng phương pháp quy nạp này để chứng minh.
* Ví dụ: Tính tổng Sn = 1 + 3 + 5 + . . . + (2n -1)
° Hướng dẫn: (sử dụng phương pháp quy nạp)
– Đầu tiên, ta thử với n = 1, ta có: S1 = (2.1 – 1) = 1
Thử với n = 2, ta có: S2 = (2.1 – 1) + (2.2 – 1) = 1+ 3 = 4 = 22
Thử với n= 3, ta có: S3 = (2.1 – 1) + (2.2 – 1) + (2.3 – 1)= 1+ 3 + 5 = 9 = 32
… … …
– Ta dự đoán: Sn = 1 + 3 + 5 + . . . + (2n -1) = n2
• Phương pháp quy nạp: Sn = 1 + 3 + 5 + . . . + (2n -1) = n2 (*)
Với n = 1; S1 = 1 (đúng)
Giả sử đúng với n = k (k≠1), tức là:
Sk =1 + 3 + 5 + . . . + (2k -1) = k2 (1)
Ta cần chứng minh (*) đúng với n = k+1, tức là:
Sk+1 = 1 + 3 + 5 + . . . + (2k-1) + (2k+1) = (k+1)2
Vì ta đã giải sử Sk đúng nên ta đã có (1), từ đây ta biến đổi để xuất hiện (2), (1) còn được gọi là giải thiết quy nạp.
1 + 3 + 5 + . . . + (2k -1) = k2
1 + 3 + 5 + . . . + (2k-1) + (2k+1) = k2+ (2k+1) (cộng 2k+1 vào 2 vế).
Từ đó ⇒ 1 + 3 + 5 + . . . + (2k-1) + (2k+1) = k2 + 2k + 1 = (k+1)2
• Tương tự như vậy, ta có thể chứng minh các kết quả sau bằng phương pháp quy nạp toán học:
1) 
2) 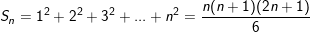
3) 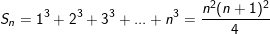
4) 
II. Dạng toán Tính tổng dãy sử dụng phương pháp khử liên tiếp
– Giả sử cần tính tổng: Sn = a1 + a2 + . . . + an (*) mà ta có thể biểu diễn ai, i =1,2,3,…,n qua hiệu của 2 số hạng liên tiếp của 1 dãy khác, cụ thể như sau:
a1 = b1 – b2
a2 = b2 – b3
… … …
an = bn – bn+1
⇒ Khi đó ta có: Sn = (b1 – b2) + (b2 – b3)+…+(bn – bn+1) = b1 – bn+1
* Ví dụ 1: Tính tổng:

° Hướng dẫn: – Ta có:
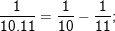
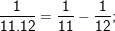
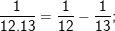 …;
…; 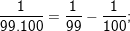
⇒
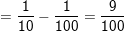
• Dạng tổng quát:
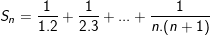
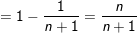
* Ví dụ 2: Tính tổng:

° Hướng dẫn: – Ta có:
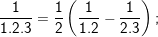
 ;…;
;…; 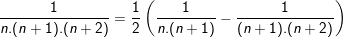

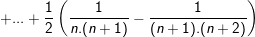
![small Leftrightarrow S_{n}=frac{1}{2}left [ frac{1}{1.2}-frac{1}{2.3}+frac{1}{2.3}-frac{1}{3.4}+...+frac{1}{n(n+1)}-frac{1}{(n+1)(n+2)} ight ] 1568138664ow7bw822nv 1633221189 1](https://tmdl.edu.vn/wp-content/uploads/2023/03/1568138664ow7bw822nv_1633221189-1.gif)
![small Leftrightarrow S_{n}=frac{1}{2}left [ frac{1}{1.2}-frac{1}{(n+1)(n+2)} ight ]=frac{n(n+3)}{4(n+1)(n+2)} 1568138666by0vs6xbxe 1633221190 1](https://tmdl.edu.vn/wp-content/uploads/2023/03/1568138666by0vs6xbxe_1633221190-1.gif)
* Ví dụ 3: Tính tổng:
![small S_{n}=frac{3}{(1.2)^{2}}+frac{5}{(2.3)^{2}}+...+frac{2n+1}{left [n(n+1) ight ]^{2}} 1568173599sw7cq68daa 1633221190 1](https://tmdl.edu.vn/wp-content/uploads/2023/03/1568173599sw7cq68daa_1633221190-1.gif)
° Hướng dẫn: – Ta có:
![small frac{2i+1}{left [i(i+1) ight ]^{2}}=frac{1}{i^{2}}-frac{1}{(i+1)^{2}};i=1;2;3;...;n 1568173601jstq5mocxe 1633221190 1](https://tmdl.edu.vn/wp-content/uploads/2023/03/1568173601jstq5mocxe_1633221190-1.gif)
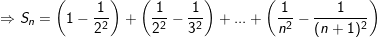
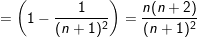
III. Dạng toán giải phương trình với ẩn là tổng cần tìm
• Dạng toán này vận dựng 2 phương pháp giới thiệu ở trên
* Ví dụ 1: Tính tổng: S = 1 + 2 + 22 + . . . + 2100 (*)
° Hướng dẫn:
* Cách 1: Ta viết lại S như sau:
S = 1 + 2(1 + 2 + 22 + . . . + 299)
S = 1 + 2(1 + 2 + 22 + . . . + 299 + 2100 – 2100)
⇒ S = 1+ 2(S – 2100) = 1+ 2S – 2101
⇒ S = 2101 – 1
* Cách 2: Nhân 2 vế với 2, ta được:
2S = 2(1 + 2 + 22 + . . . + 2100)
⇔ 2S = 2 + 22 + 23 + . . . 2101 (**)
– Lấy (**) trừ đi (*) ta được:
2S – S = (2 + 22 + 23 + . . . 2101) – (1 + 2 + 22 + . . . + 2100)
⇔ S = 2101 – 1.
• Tổng quát cho dạng toán này như sau:
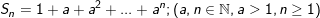
Ta nhân cả 2 vế của Sn với a. Rồi TRỪ vế với vế ta được: 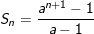
* Ví dụ 2: Tính:
S = 1 – 2 + 22 – 23 + 24 – . . . – 299 + 2100
° Hướng dẫn:– Ta có:
2S = 2(1 – 2 + 22 – 23 + 24 – . . . – 299 + 2100)
⇔ 2S = 2 – 22 + 23 – 24 + 25 – . . . – 2100 + 2101
⇔ 2S + S = (2 – 22 + 23 – 24 + 25 – . . . – 2100 + 2101) + (1 – 2 + 22 – 23 + 24 – . . . – 299 + 2100)
⇔ 3S = 2101 + 1.

• Tổng quát cho dạng toán này như sau:

Ta nhân cả 2 vế của Sn với a. Rồi CỘNG vế với vế ta được: 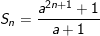
* Ví dụ 3: Tính tổng:
S = 1 + 32 + 34 + . . . + 398 + 3100 (*)
° Hướng dẫn:
– Với bài toán này, mục tiêu là nhân 2 vế của S với một số nào đó mà khi trừ vế với về thì ta được các số khử (triệu tiêu) liên tiếp.
– Đối với bài này, ta thấy số mũ của 2 số liên tiếp cách nhau 2 đơn vị nên ta nhân hai vế với 32 rồi áp dụng phương pháp khử liên tiếp.
S = 1 + 32 + 34 + . . . + 398 + 3100
⇔ 32.S = 32(1 + 32 + 34 + . . . + 398 + 3100)
⇔ 9S= 32 + 34 + . . . + 3100 + 3102 (**)
– Ta Trừ vế với vế của (**) cho (*) được:
9S-S= (32 + 34 + . . . + 3100 + 3102) – (1 + 32 + 34 + . . . + 398 + 3100)
⇔ 8S = 3102 – 1

• Tổng quát cho dạng toán này như sau:
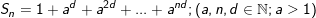
Ta nhân cả 2 vế của Sn với ad . Rồi TRỪ vế với vế ta được:
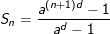
* Ví dụ 4: Tính:
S = 1 – 23 + 26 – 29+ . . . + 296 – 299 (*)
° Hướng dẫn:
– Lũy thừa các số liên tiếp cách nhau 3 đơn vị, nhân 2 vế với 23 ta được:
23.S = 23.(1 – 23 + 26 – 29+ . . . + 296 – 299)
⇒ 8S = 23 – 26 + 29 – 212+ . . . + 299 – 2102 (**)
– Ta CỘNG vế với vế (**) với (*) được:
8S + S = (23 – 26 + 29 – 212+ . . . + 299 – 2102)+(1 – 23 + 26 – 29+ . . . + 296 – 299)
⇔ 9S = 1 – 2102 
• Tổng quát cho dạng toán này như sau:
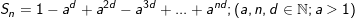
Ta nhân cả 2 vế của Sn với ad . Rồi CỘNG vế với vế ta được:
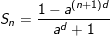
III. Dạng toán vận dụng công thức tính tổng các số hạng của dãy số cách đều.
• Đối với dạng này ở bậc học cao hơn như THPT các em sẽ có công thức tính theo cấp số cộng hoặc cấp số nhân, còn với lớp 6 các em dựa vào cơ sở lý thuyết sau:
– Để đếm được số hạng cảu 1 dãy số mà 2 số hạng liên tiếp cách đều nhau 1 số đơn vị ta dùng công thức:
Số số hạng = [(số cuối – số đầu):(khoảng cách)] + 1
– Để tính Tổng các số hạng của một dãy mà 2 số hạng liên tiếp cách đều nhau 1 số đơn vị ta dùng công thức:
Tổng = [(số đầu + số cuối).(số số hạng)]:2
* Ví dụ 1: Tính tổng: S = 1 + 3 + 5 + 7 + … + 39
° Hướng dẫn:
– Số số hạng của S là: (39-1):2+1 = 19+1 = 20.
S = [20.(39+1)]:2 = 10.40 = 400.
* Ví dụ 2: Tính tổng: S = 2 + 5 + 8 + … + 59
° Hướng dẫn:
– Số số hạng của S là:(59-2):3+1 = 19+1 = 20.
S = [20.(59+2)]:2 = 10.61 = 610.
IV. Dạng toán tổng hợp vận dụng các tổng đã biết
• Ký hiệu: 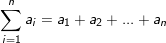
• Tính chất:


* Ví dụ: Tính tổng: Sn = 1.2 + 2.3 + 3.4 +…+n(n+1)
° Hướng dẫn:
– Ta có: 
– Mặt khác, lại có:
 (theo PP quy nạp ở mục I).
(theo PP quy nạp ở mục I).
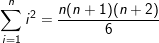 (theo PP quy nạp ở mục I)
(theo PP quy nạp ở mục I)

V. Một số bài tập luyện tập về tính tổng dãy số có quy luật
Bài tập 1: Tính tổng: S = 3 + 8 + 13 + 18 + … + 228
Bài tập 2: Tính các tổng sau:
a) S = 6 + 62 + 63 +…+ 699 + 6100
b) S = 5 + 11 + 17 +…+ 95 + 101
c) 
d) 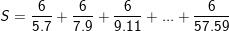
Bài tập 3: Chứng minh
a) 1.4 + 4.7 + 7.10 +…+(3n-2)(3n+1) = n(n+1)2
b) 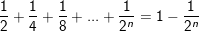
Hy vọng với bài viết hệ thống lại Các dạng toán Tính tổng Dãy số lũy thừa có quy luật và bài tập vận dụng ở trên hữu ích cho các em. Mọi góp ý và thắc mắc các em vui lòng để lại bình luận dưới bài viết để Trường Trung Cấp Nghề Thương Mại Du Lịch Thanh Hoá ghi nhận và hỗ trợ, chúc các em học tập tốt !
Các dạng toán tính tổng dãy số lũy thừa có quy luật
Các dạng toán tính tổng dãy số lũy thừa có quy luật là một trong những chuyên đề có khá nhiều bài tập được gọi là “khó nhằn” và gây ‘căng thẳng đầu óc’ cho các bạn học sinh lớp 6, đây có thể coi là dạng toán dành cho học sinh khá giỏi. Vì vậy, nhằm giúp các em học sinh “giải tỏa được căng thẳng” khi gặp các dạng toán về tính tổng dãy số lũy thừa có quy luật, trong bài viết này chúng ta hãy cùng hệ thống lại một số dạng toán này cùng công thức và cách giải, sau đó vận dụng làm các bài tập. I. Dạng toán tính tổng dãy sử dụng phương pháp quy nạp. – Đối với 1 số trường hợp khi tính tổng hữu hạn: Sn = a1 + a2 + . . . + an (*) khi mà ta có thể biết được kết quả (đề bài toán cho ta biết kết quả hoặc ta dự đoán được kết quả), thì ta sử dụng phương pháp quy nạp này để chứng minh. * Ví dụ: Tính tổng Sn = 1 + 3 + 5 + . . . + (2n -1) ° Hướng dẫn: (sử dụng phương pháp quy nạp) – Đầu tiên, ta thử với n = 1, ta có: S1 = (2.1 – 1) = 1 Thử với n = 2, ta có: S2 = (2.1 – 1) + (2.2 – 1) = 1+ 3 = 4 = 22 Thử với n= 3, ta có: S3 = (2.1 – 1) + (2.2 – 1) + (2.3 – 1)= 1+ 3 + 5 = 9 = 32 … … … – Ta dự đoán: Sn = 1 + 3 + 5 + . . . + (2n -1) = n2 • Phương pháp quy nạp: Sn = 1 + 3 + 5 + . . . + (2n -1) = n2 (*) Với n = 1; S1 = 1 (đúng) Giả sử đúng với n = k (k≠1), tức là: Sk =1 + 3 + 5 + . . . + (2k -1) = k2 (1) Ta cần chứng minh (*) đúng với n = k+1, tức là: Sk+1 = 1 + 3 + 5 + . . . + (2k-1) + (2k+1) = (k+1)2 Vì ta đã giải sử Sk đúng nên ta đã có (1), từ đây ta biến đổi để xuất hiện (2), (1) còn được gọi là giải thiết quy nạp. 1 + 3 + 5 + . . . + (2k -1) = k2 1 + 3 + 5 + . . . + (2k-1) + (2k+1) = k2+ (2k+1) (cộng 2k+1 vào 2 vế). Từ đó ⇒ 1 + 3 + 5 + . . . + (2k-1) + (2k+1) = k2 + 2k + 1 = (k+1)2 • Tương tự như vậy, ta có thể chứng minh các kết quả sau bằng phương pháp quy nạp toán học: 1) 2) 3) 4) II. Dạng toán Tính tổng dãy sử dụng phương pháp khử liên tiếp – Giả sử cần tính tổng: Sn = a1 + a2 + . . . + an (*) mà ta có thể biểu diễn ai, i =1,2,3,…,n qua hiệu của 2 số hạng liên tiếp của 1 dãy khác, cụ thể như sau: a1 = b1 – b2 a2 = b2 – b3 … … … an = bn – bn+1 ⇒ Khi đó ta có: Sn = (b1 – b2) + (b2 – b3)+…+(bn – bn+1) = b1 – bn+1 * Ví dụ 1: Tính tổng: ° Hướng dẫn: – Ta có: …; ⇒ • Dạng tổng quát: * Ví dụ 2: Tính tổng: ° Hướng dẫn: – Ta có: ;…; * Ví dụ 3: Tính tổng: ° Hướng dẫn: – Ta có: III. Dạng toán giải phương trình với ẩn là tổng cần tìm • Dạng toán này vận dựng 2 phương pháp giới thiệu ở trên * Ví dụ 1: Tính tổng: S = 1 + 2 + 22 + . . . + 2100 (*) ° Hướng dẫn: * Cách 1: Ta viết lại S như sau: S = 1 + 2(1 + 2 + 22 + . . . + 299) S = 1 + 2(1 + 2 + 22 + . . . + 299 + 2100 – 2100) ⇒ S = 1+ 2(S – 2100) = 1+ 2S – 2101 ⇒ S = 2101 – 1 * Cách 2: Nhân 2 vế với 2, ta được: 2S = 2(1 + 2 + 22 + . . . + 2100) ⇔ 2S = 2 + 22 + 23 + . . . 2101 (**) – Lấy (**) trừ đi (*) ta được: 2S – S = (2 + 22 + 23 + . . . 2101) – (1 + 2 + 22 + . . . + 2100) ⇔ S = 2101 – 1. • Tổng quát cho dạng toán này như sau: Ta nhân cả 2 vế của Sn với a. Rồi TRỪ vế với vế ta được: * Ví dụ 2: Tính: S = 1 – 2 + 22 – 23 + 24 – . . . – 299 + 2100 ° Hướng dẫn:- Ta có: 2S = 2(1 – 2 + 22 – 23 + 24 – . . . – 299 + 2100) ⇔ 2S = 2 – 22 + 23 – 24 + 25 – . . . – 2100 + 2101 ⇔ 2S + S = (2 – 22 + 23 – 24 + 25 – . . . – 2100 + 2101) + (1 – 2 + 22 – 23 + 24 – . . . – 299 + 2100) ⇔ 3S = 2101 + 1. • Tổng quát cho dạng toán này như sau: Ta nhân cả 2 vế của Sn với a. Rồi CỘNG vế với vế ta được: * Ví dụ 3: Tính tổng: S = 1 + 32 + 34 + . . . + 398 + 3100 (*) ° Hướng dẫn: – Với bài toán này, mục tiêu là nhân 2 vế của S với một số nào đó mà khi trừ vế với về thì ta được các số khử (triệu tiêu) liên tiếp. – Đối với bài này, ta thấy số mũ của 2 số liên tiếp cách nhau 2 đơn vị nên ta nhân hai vế với 32 rồi áp dụng phương pháp khử liên tiếp. S = 1 + 32 + 34 + . . . + 398 + 3100 ⇔ 32.S = 32(1 + 32 + 34 + . . . + 398 + 3100) ⇔ 9S= 32 + 34 + . . . + 3100 + 3102 (**) – Ta Trừ vế với vế của (**) cho (*) được: 9S-S= (32 + 34 + . . . + 3100 + 3102) – (1 + 32 + 34 + . . . + 398 + 3100) ⇔ 8S = 3102 – 1 • Tổng quát cho dạng toán này như sau: Ta nhân cả 2 vế của Sn với ad . Rồi TRỪ vế với vế ta được: * Ví dụ 4: Tính: S = 1 – 23 + 26 – 29+ . . . + 296 – 299 (*) ° Hướng dẫn: – Lũy thừa các số liên tiếp cách nhau 3 đơn vị, nhân 2 vế với 23 ta được: 23.S = 23.(1 – 23 + 26 – 29+ . . . + 296 – 299) ⇒ 8S = 23 – 26 + 29 – 212+ . . . + 299 – 2102 (**) – Ta CỘNG vế với vế (**) với (*) được: 8S + S = (23 – 26 + 29 – 212+ . . . + 299 – 2102)+(1 – 23 + 26 – 29+ . . . + 296 – 299) ⇔ 9S = 1 – 2102 • Tổng quát cho dạng toán này như sau: Ta nhân cả 2 vế của Sn với ad . Rồi CỘNG vế với vế ta được: III. Dạng toán vận dụng công thức tính tổng các số hạng của dãy số cách đều. • Đối với dạng này ở bậc học cao hơn như THPT các em sẽ có công thức tính theo cấp số cộng hoặc cấp số nhân, còn với lớp 6 các em dựa vào cơ sở lý thuyết sau: – Để đếm được số hạng cảu 1 dãy số mà 2 số hạng liên tiếp cách đều nhau 1 số đơn vị ta dùng công thức: Số số hạng = [(số cuối – số đầu):(khoảng cách)] + 1 – Để tính Tổng các số hạng của một dãy mà 2 số hạng liên tiếp cách đều nhau 1 số đơn vị ta dùng công thức: Tổng = [(số đầu + số cuối).(số số hạng)]:2 * Ví dụ 1: Tính tổng: S = 1 + 3 + 5 + 7 + … + 39 ° Hướng dẫn: – Số số hạng của S là: (39-1):2+1 = 19+1 = 20. S = [20.(39+1)]:2 = 10.40 = 400. * Ví dụ 2: Tính tổng: S = 2 + 5 + 8 + … + 59 ° Hướng dẫn: – Số số hạng của S là:(59-2):3+1 = 19+1 = 20. S = [20.(59+2)]:2 = 10.61 = 610. IV. Dạng toán tổng hợp vận dụng các tổng đã biết • Ký hiệu: • Tính chất: * Ví dụ: Tính tổng: Sn = 1.2 + 2.3 + 3.4 +…+n(n+1) ° Hướng dẫn: – Ta có: – Mặt khác, lại có: (theo PP quy nạp ở mục I). (theo PP quy nạp ở mục I) V. Một số bài tập luyện tập về tính tổng dãy số có quy luật Bài tập 1: Tính tổng: S = 3 + 8 + 13 + 18 + … + 228 Bài tập 2: Tính các tổng sau: a) S = 6 + 62 + 63 +…+ 699 + 6100 b) S = 5 + 11 + 17 +…+ 95 + 101 c) d) Bài tập 3: Chứng minh a) 1.4 + 4.7 + 7.10 +…+(3n-2)(3n+1) = n(n+1)2 b) Hy vọng với bài viết hệ thống lại Các dạng toán Tính tổng Dãy số lũy thừa có quy luật và bài tập vận dụng ở trên hữu ích cho các em. Mọi góp ý và thắc mắc các em vui lòng để lại bình luận dưới bài viết để Trường Trung Cấp Nghề Thương Mại Du Lịch Thanh Hoá ghi nhận và hỗ trợ, chúc các em học tập tốt ! Đăng bởi: Trường Trung Cấp Nghề Thương Mại Du Lịch Thanh Hoá Chuyên mục: Giáo Dục
Bản quyền bài viết thuộc Trường Trung Cấp Nghề Thương Mại Du Lịch Thanh Hoá. Mọi hành vi sao chép đều là gian lận!
Nguồn chia sẻ: https://tmdl.edu.vn https://tmdl.edu.vn/cac-dang-toan-tinh-tong-day-so-luy-thua-co-quy-luat-va-bai-tap/
Trang chủ: tmdl.edu.vn
Danh mục bài: Giáo dục