Bài tập Hệ thức lượng trong tam giác vuông có lời giải. Hệ thức lượng trong tam giác vuông là một trong những kiến thức trọng tâm mà các em cần nắm thật vững, vì dạng bài tập liên quan tới hệ thức lượng trong tam giác vuông thường xuất hiện trong nhiều bài thi và kiểm tra.
Bài viết dưới đây chúng ta cùng hệ thống lại các công thức hệ thức lượng trong tam giác vuông, qua đó vận dụng các công thức này giải một số dạng bài tập minh họa để hiểu rõ hơn, ghi nhớ tốt hơn các hệ thức quan trọng này.
Bạn đang xem bài: Bài tập Hệ thức lượng trong tam giác vuông có lời giải – Toán lớp 9 chuyên đề
I. Hệ thức lượng trong tam giác vuông cần nhớ
Cho ΔABC có vuông tại A (góc A bằng 900) như hình sau:
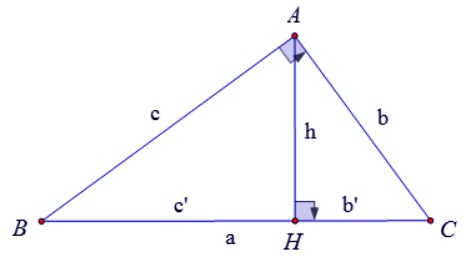
Có: AH ⊥ BC, AB = c, AC = b, BC = a, AH = h, thì:
• BH = c’ được gọi là hình chiếu của AB xuống BC
• CH = b’ được gọi là hình chiếu của AC xuống BC
Khi đó, ta có:
1) AB2 = BH.BC hay c2 = a.c’
AC2 = CH.BC hay b2 = a.b’
2) AH2 = CH.BH hay h2 = b’.c’
3) AB.AC = AH.BC hay b.c = a.h
4) 1/(AH)2 = 1/(AB)2 + 1/(AC)2 hay 1/h2 = 1/b2 + 1/c2
5) AB2 + AC2 = BC2 hay b2 + c2 = a2 (Định lý Pytago)
II. Tỉ số lượng giác của góc nhọn
1. Định nghĩa:
– Cho tam giác ABC (vuông tại A) gồm cạnh đối, cạnh huyền và cạnh kề:
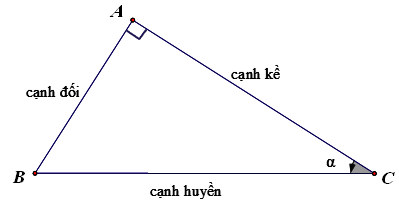
• sinα = Đối/Huyền = AB/BC
• cosα = Kề/Huyền = AC/BC
• tanα = Đối/Kề = AB/AC
• cotα = Kề/Đối = AC/AB
2. So sánh các tỉ số lượng giác
a) Cho α,β là hai góc nhọn. Nếu α < β thì
• sinα < sinβ; tanα < tanβ
• cosα > cosβ; cotα > cotβ
b) sinα < tanα; cosα < cotα
→ Các bạn có thể tham khảo đầy đủ công thức ở bài viết: Công thức hệ thức lượng trong tam giác vuông
III. Bài tập hệ thức lượng trong tam giác vuông
* Bài tập 1: Cho tam giác ABC vuông tại A. Trong đó AB = 12cm, AC = 9cm. Tính các tỉ số lượng giác của góc B, từ đó suy ra tỉ số lượng giác của góc C.
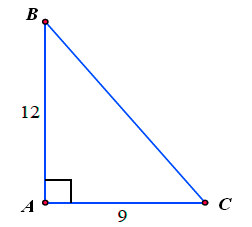* Lời giải:
– Theo định lí pitago ta có:
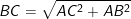
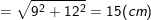
Vậy, ta có:
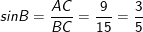
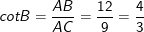
Vì góc B và góc C là hai góc phụ nhau:
* Bài tâp 2: Cho tam giác ABC vuông tại A, đường cao AH. Biết AC = 20 cm, BH = 9cm. Tính độ dài BC và AH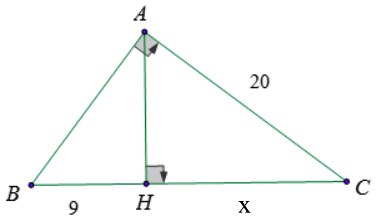
> Lời giải:
• Ta đặt HC = x (x>0).
Áp dụng hệ thức AC2 = BC.HC, ta được:
⇒ 202 = (9 + x)x
⇔ x2 + 9x – 400 = 0
⇔ (x + 25)(x – 16) = 0
⇔ x = -25 (loại) hoặc x = 16
Vậy độ dài của cạnh huyền BC là:
BC = BH + HC = 9 + 16 = 25 cm
– Ta có: AH2 = HB.HC = 9.25 = 32.52 = 152
Nên chiều dài đường cao AH là: AH = 15 (cm)
* Bài tập 3: Cho tam giác ABC vuông tại A, AB : AC = 7 : 24, BC = 625 cm. Tính độ dài hình chiếu của hai cạnh góc vuông trên cạnh huyền.
* Lời giải:
– Ta có hình minh họa như sau:
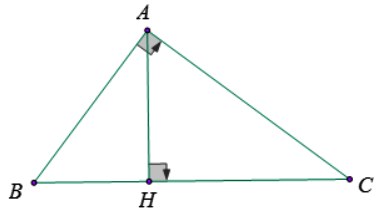
Vẽ AH ⊥ BC, thì ta có:
AB2 = BH.BC ;
AC2 = CH.BC ;
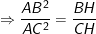
Nên ta có:
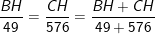
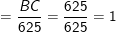
(sử dụng tính chất tỉ lệ thức: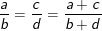 
)
Suy ra: BH = 49.1 = 49;
CH = 576.1 = 576
* Bài tập 4: Cho tam giác ABC vuông tại A, BC = a, CA = b, AB = c.
Chứng minh rằng: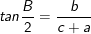 
* Lời giải:
– Ta vẽ hình như sau:
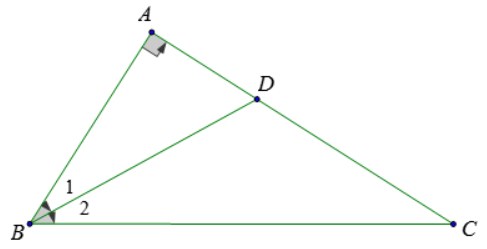Từ góc B vẽ tia phân giác BD. Khi đó, ta có:
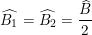
Theo tính chất tia phân giác ta có: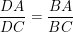 
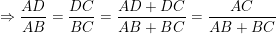
Xét tam giác ABD vuông tại A có:
Vậy ta có điều cần chứng minh.
* Bài tập 5: Chứng minh giá trị các biểu thức sau không phụ thuộc vào giá trị của các góc nhọn α, β
a) cos2 α.cos2 β + cos2 α.sin2 β + sin2 α
b) 2(sinα – cosα )2 – (sinα + cosα )2 + 6sinα.cosα
c) (tanα – cotα )2 – (tanα + cotα )2
* Lời giải:
a) cos2 α.cos2 β + cos2 α.sin2 β + sin2 α
= cos2 = cos2 α(cos2 β + sin2 β) + sin2 α
= cos2 α.1 + sin2 α
= 1
b) 2(sinα – cosα )2 – (sinα + cosα )2 + 6 sinα.cosα
= 2(1 – 2sinα.cosα ) – (1 + 2sinα.cosα ) + 6sinα.cosα
= 1 – 6sinα.cosα + 6sinα.cosα
= 1
c) (tanα – cotα )2 – (tanα + cotα )2
= (tan2 α – 2 tanα.cotα + cot2 α) – (tan2 α + 2 tanα.cotα + cot2 α )
= -4 tanα.cotα
= -4.1 = -4
Hy vọng qua nội dung về Hệ thức lượng trong tam giác vuông lớp 9 và bài tập toán minh họa ở trên ở trên giúp các em ghi nhớ tốt hơn, nắm vững hơn, và dễ dàng vận dụng các hệ thức lượng này vào các dạng bài tập tương tự. Mọi góp ý và thắc mắc các em hãy để lại nhận xét dưới bài viết để Hay Học Hỏi ghi nhận và hỗ trợ, chúc các em học tốt.
Bản quyền bài viết thuộc trường Trường Trung Cấp Nghề Thương Mại Du Lịch Thanh Hoá. Mọi hành vi sao chép đều là gian lận!
Nguồn chia sẻ: Trường Tmdl.edu.vn (tmdl.edu.vn)
Trang chủ: tmdl.edu.vn
Danh mục bài: Giáo dục
