Các tính chất và dấu hiệu chia hết ở lớp 6 giúp các em dễ dàng vận dụng để thực hiện các phép tính trên số tự nhiên một cách nhanh và chính xác.
Bài viết này sẽ hệ thống lại một số bài toán vận dụng tính chất và dấu hiệu chia hết cùng lời giải, qua đó giúp các em dễ dàng ghi nhớ và vận dụng khi gặp các bài toán chia hết.
Bạn đang xem bài: Các bài toán vận dụng tính chất và dấu hiệu chia hết có lời giải – Toán lớp 6
I. Tóm tắt lý tuyết về tính chất và dấu hiệu chia hết
1. Dấu hiệu chia hết cơ bản
a) Dấu hiệu chia hết cho 2
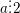⇔ a có chữ số tận cùng bằng 0; 2; 4; 6; 8.
b) Dấu hiệu chia hết cho 5
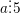⇔ a có chữ số tận cùng bằng 0; 5.
c) Dấu hiệu chia hết cho 3 (hoặc 9)
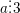hoặc 
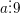⇔ a có tổng các chữ số của a chia hết cho 3 (hoặc 9).
2. Dấu hiệu chia hết nâng cao
a) Dấu hiệu chia hết cho 4 (hoặc 25)
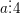hoặc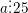 
⇔ Hai chữ số tận cùng của nó tạo thành một số chia hết cho 4 (hoặc 25).
b) Dấu hiệu chia hết cho 8 (hoặc 125)
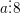hoặc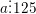 
⇔ Ba chữ số tận cùng của nó tạo thành một số chia hết cho 8 (hoặc 125).
c) Dấu hiệu chia hết cho 11
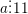⇔ Tổng các chữ số hàng lẻ trừ đi tổng các chữ số hàng chẵn (hoặc ngược lại) chia hết cho 11.
3. Tính chất của chia hết cơ bản.
a) Tính chất chung
– Bất kỳ số nào khác 0 cũng chia hết cho chính nó
– Nếu a chia hết cho b và b chia hết cho c thì a chia hết cho c
– Số 0 chia hết cho mọi số b khác 0
– Bất cứ só nào cũng chia hết cho 1
b) Các tính chất khác
– a chia hết cho a với mọi a là số tự nhiên khác 0: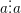 
, 
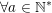
– Nếu a chia hết cho b và b chia hết cho a thì a=b.
– Nếu a và b cùng chia hết cho m thì a+b chia hết cho m; a-b chia hết cho m
– Nếu một trong hai số a và b chia hết cho m, số kia không chia hết cho m thì a+b không chia hết cho m, a-b không chia hết cho m
– Nếu a chia hế cho b và a chia hết cho c mà (b;c)=1 thì a chia hết cho b.c
– Nếu a.b chia hết cho c và (b,c)=1 thì a chia hế cho c
– Nếu a chia hiết cho m thì k.a chia hết cho m với mọi k là số tự nhiên
– Nếu a chia hết cho m và b chia hết cho n thì a.b chia hết cho m.n
– Nếu a.b chia hết cho m và m là số nguyên tốt thì a chia hết cho m hoặc b chia hết cho m
– Nếu a chia hết cho m thì an chia hết cho m với mọi n là số tự nhiên
– Nếu a chia hết cho b thì an chia hết cho bn với mọi n là số tự nhiên
4. Tính chất chia hết nâng cao
° 
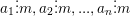
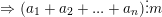
° a1 không chia hết cho m còn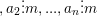 
thì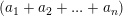 
không chia hết cho m
° 
° 
° 
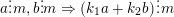
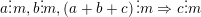
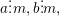
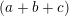không chia hết cho m ⇒ c không chia hết cho m.
II. Các bài toán vận dụng tính chất và dấu hiệu chia hết
° Dạng 1: Chứng minh số a chia hết cho số b
* Phương pháp:
– Dựa vào các dấu hiệu và tính chất chia hết
♦ Ví dụ 1: Không thực hiện phép tính chứng tỏ rằng
a) 26.2020 chia hết cho 13
b) 2014.2019 chia hết cho 3
c) 1411.2020 chia hết cho 17
♠ Hướng dẫn
a) Ta có: 26.2020 = 2.13.2020 
13 (vì 13 13, theo tính chất)
b) Ta có: 2014.2019 = 2014.3.673 3 (vì 3 3, theo tính chất)
c) Ta có: 1411.2020 = 17.83.2020 17 (vì 17 17, theo tính chất)
♦ Ví dụ 2: Chứng minh rằng (7a)2020 chia hết cho 49 ∀a∈N.
♠ Hướng dẫn
– Ta có: (7a)2020 = 72020.a2020 = 72.72018.a2020 = 49.72018.a2020
Vì 49 49 nên 49.72018.a2020 49
⇒(7a)2020 chia hết cho 49 ∀a∈N.
° Dạng 2: Tìm điều kiện để số a chia hết cho số b
* Phương pháp:
– Vận dụng các tính chất và dấu hiệu chia hết
♦ Ví dụ 1: Điền vào * để
a)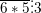 
b)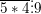 
♠ Hướng dẫn
a) Vận dụng dấu hiệu chia hết để 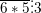⇔ (6+*+5) = (11+*) phải chia hết cho 3 ⇒ * ∈ {1;4;7}
b) Vận dụng dấu hiệu chia hết để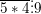 
⇔ (9+*) phải chia hết cho 9 ⇒ * ∈ {0;9}
♦ Ví dụ 2: Tìm chữ số a, b sao cho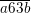 
đồng thời chia hết cho 2,3,5 và 9.
♠ Hướng dẫn
– Từ dấu hiệu chia hết ta thấy, 2 và 5 liên quan đến chữ số tận cùng, sau đó ta xét tổng các chữ số phải chia hết cho 9 (vì chia hết cho 9 là chia hết cho 3).
– Ta có: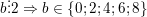 
và 
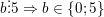
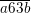⇒ chia hết cho 2 và 5 thì b = 0.
– Để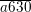 
chia hết cho 3 và 9 ⇒ (a + 6 + 3 + 0) 
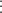9 ⇒ a ∈ {0;9} ⇒ a = 9.
(vì số 0 đứng đầu không có nghĩa)
– Kết luận: a=9; b=0 thì 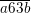đồng thời chia hết cho 2;3;5;9.
♦ Ví dụ 3: Tìm a để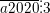 
nhưng không chia hết cho 9.
♠ Hướng dẫn
– Từ dấu hiệu chia hết cho 3 và chia hết cho 9, ta có:
⇒ (a+2+0+2+0) chia hết cho 3
⇒ (a+4) chia hết cho 3
⇒ a = 2
– Kết luận: Với a = 2 thì 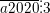mà không chia hết cho 9.
° Dạng 3: Chứng minh một biểu thức chia hết cho một số
* Phương pháp:
– Vận dụng các tính chất tổng chia hết, hiệu chia hết
♦ Ví dụ 1: Chứng minh rằng S = 5 + 52 + 53 +…+ 599 + 5100 chia hết cho 6.
♠ Hướng dẫn
– Ta có: S = 5 + 52 + 53 +…+ 599 + 5100 = 5(1+5) + 53(1+5) +…+ 599(1+5) = 6.(5 + 53 + 55 +…+ 599)
Vì 6 6 nên S chia hết cho 6 (theo tính chất).
♦ Ví dụ 2: Chứng minh rằng
a) 36 + 81 + 171 chia hết cho 9
b) 135 + 275 + 335 chia hết cho 5
c) 2124 – 204 chia hết cho 4
d) 6433 – 2058 chia hết cho 7
♠ Hướng dẫn
a) Ta có: 36 9; 81 9; 171 9 nên (36 + 81 + 171) 9 (theo tính chất chia hết của một tổng)
b) Ta có: 135 5; 275 5; 335 5 nên (135 + 275 + 335) 5 (theo tính chất chia hết của một tổng)
c) Ta có: 2124 4; 204 4 nên (2124 – 204) 4 (theo tính chất chia hết của một hiệu)
d) Ta có: 6433 7; 2058 7 nên (6433 – 2058) 7 (theo tính chất chia hết của một hiệu)
♦ Ví dụ 3: Chứng minh rằng
a) A = 1 + 3 + 32 +…+ 311 chia hết cho 40.
b) B = 5 + 52 + 53 +…+ 58 chia hết cho 30.
♠ Hướng dẫn
a) Ta có: A = 1 + 3 + 32 +…+ 311 = (1 + 3 + 32 + 33) + 34(1 + 3 + 32 + 33) + 38(1 + 3 + 32 + 33) = (1 + 3 + 32 + 33)(1 + 34 + 38) = 40.(1 + 34 + 38)
⇒ A chia hết cho 40.
a) Ta có: B = 5 + 52 + 53 +…+ 58 = 5(1 + 5) + 52(5+25) + 54(5+25) + 56(5+25) = 30(1 + 52 + 54 +56).
⇒ B chia hết cho 30.
° Dạng 4: Một số dạng bài toán chứng minh khác
* Phương pháp:
– Vận dụng các tính chất và dấu hiệu chia hết.
♦ Ví dụ 1: Chứng minh tổng 3 số tự nhiên liên tiếp chia hết cho 3
♠ Hướng dẫn
– Gọi ba số tự nhiên liên tiếp là: a, a+1 và a+2
⇒ Tổng ba số là: a + a + 1 + a + 2 = (a + a + a) + (1 + 2) = (3a + 3)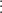 
3 (theo tính chất chia hết của 1 tổng)
♦ Ví dụ 2: Chứng minh tích của 2 số tự nhiên liên tiếp chia hết cho 2
♠ Hướng dẫn
– Gọi hai số tự nhiên liên tiếp là: b, b+1
⇒ Tích hai số là: b(b + 1)
– Nếu b chẵn thì b=2k (k∈N) ⇒ 2k(2k+1) 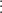2 (do 2k 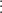2)
– Nếu b lẻ thì b=2k+1 (k∈N) ⇒ (2k+1)(2k+1+1) = (2k+1)(2k+2) 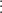2 (do (2k 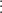+ 2) 2)
⇒ Tích của 2 số tự nhiên liên tiếp chia hết cho 2.
♦ Ví dụ 3: Chứng minh tích của 2 số tự nhiên chẵn liên tiếp luôn chia hết cho 8
♠ Hướng dẫn
– Gọi hai số chẵn liên tiếp là: 2a và 2a+2 (a∈N)
– Khi đó ta có: 2a.(2a+2) = 4a.(a+1)
– Ta thấy, a(a+1) là hai số tự nhiên liên tiếp nên theo ví dụ 2 thì a(a+1) chia hết cho 2.
⇒ 4.a.(a+1) chia hết cho 4.2
⇒ 4.a.(a+1) chia hết cho 8.
– Kết luận: 2a.(2a+2) luôn chia hế cho 8, (∀a∈N).
♦ Ví dụ 4: Chứng minh rằng với mọi số tự nhiên a thì tích (a + 3).(a +6) chia hết cho 2.
♠ Hướng dẫn
◊ Với mọi số tự nhiên a (a chẵn hoặc a lẻ) ta có thể viết: a = 2k hoặc a = 2k + 1 (với k∈N).
– Với a = 2k ta có:
(a+3)(a+6) = (2k+3)(2k+6) = 2.(2k+3)(k+3) chia hết cho 2.
– Với a = 2k + 1 ta có:
(a+3).(a+6) = (2k+1 +3).(2k+1+6) = (2k+4).(2k+7) = 2.(k+2).(2k+7) chia hết cho 2.
– Vậy với mọi số tự nhiên a thì (a+3)(a+6) chia hết cho 2.
Hy vọng với bài viết hệ thống lại các bài toán vận dụng tính chất và dấu hiệu chia hết – toán 6 ở trên hữu ích cho các em. Mọi góp ý và thắc mắc các em vui lòng để lại bình luận dưới bài viết để thầy cô trường Tmdl.edu.vn ghi nhận và hỗ trợ, chúc các em học tập tốt!
Xem thêm Các tính chất và dấu hiệu chia hết ở lớp 6
Các tính chất và dấu hiệu chia hết ở lớp 6 giúp các em dễ dàng vận dụng để thực hiện các phép tính trên số tự nhiên một cách nhanh và chính xác. Bài viết này sẽ hệ thống lại một số bài toán vận dụng tính chất và dấu hiệu chia hết cùng lời giải, qua đó giúp các em dễ dàng ghi nhớ và vận dụng khi gặp các bài toán chia hết. I. Tóm tắt lý tuyết về tính chất và dấu hiệu chia hết 1. Dấu hiệu chia hết cơ bản a) Dấu hiệu chia hết cho 2 ⇔ a có chữ số tận cùng bằng 0; 2; 4; 6; 8. b) Dấu hiệu chia hết cho 5 ⇔ a có chữ số tận cùng bằng 0; 5. c) Dấu hiệu chia hết cho 3 (hoặc 9) hoặc ⇔ a có tổng các chữ số của a chia hết cho 3 (hoặc 9). 2. Dấu hiệu chia hết nâng cao a) Dấu hiệu chia hết cho 4 (hoặc 25) hoặc ⇔ Hai chữ số tận cùng của nó tạo thành một số chia hết cho 4 (hoặc 25). b) Dấu hiệu chia hết cho 8 (hoặc 125) hoặc ⇔ Ba chữ số tận cùng của nó tạo thành một số chia hết cho 8 (hoặc 125). c) Dấu hiệu chia hết cho 11 ⇔ Tổng các chữ số hàng lẻ trừ đi tổng các chữ số hàng chẵn (hoặc ngược lại) chia hết cho 11. 3. Tính chất của chia hết cơ bản. a) Tính chất chung – Bất kỳ số nào khác 0 cũng chia hết cho chính nó – Nếu a chia hết cho b và b chia hết cho c thì a chia hết cho c – Số 0 chia hết cho mọi số b khác 0 – Bất cứ só nào cũng chia hết cho 1 b) Các tính chất khác – a chia hết cho a với mọi a là số tự nhiên khác 0: , – Nếu a chia hết cho b và b chia hết cho a thì a=b. – Nếu a và b cùng chia hết cho m thì a+b chia hết cho m; a-b chia hết cho m – Nếu một trong hai số a và b chia hết cho m, số kia không chia hết cho m thì a+b không chia hết cho m, a-b không chia hết cho m – Nếu a chia hế cho b và a chia hết cho c mà (b;c)=1 thì a chia hết cho b.c – Nếu a.b chia hết cho c và (b,c)=1 thì a chia hế cho c – Nếu a chia hiết cho m thì k.a chia hết cho m với mọi k là số tự nhiên – Nếu a chia hết cho m và b chia hết cho n thì a.b chia hết cho m.n – Nếu a.b chia hết cho m và m là số nguyên tốt thì a chia hết cho m hoặc b chia hết cho m – Nếu a chia hết cho m thì an chia hết cho m với mọi n là số tự nhiên – Nếu a chia hết cho b thì an chia hết cho bn với mọi n là số tự nhiên 4. Tính chất chia hết nâng cao ° ° a1 không chia hết cho m còn thì không chia hết cho m ° ° ° không chia hết cho m ⇒ c không chia hết cho m. II. Các bài toán vận dụng tính chất và dấu hiệu chia hết ° Dạng 1: Chứng minh số a chia hết cho số b * Phương pháp: – Dựa vào các dấu hiệu và tính chất chia hết ♦ Ví dụ 1: Không thực hiện phép tính chứng tỏ rằng a) 26.2020 chia hết cho 13 b) 2014.2019 chia hết cho 3 c) 1411.2020 chia hết cho 17 ♠ Hướng dẫn a) Ta có: 26.2020 = 2.13.2020 13 (vì 13 13, theo tính chất) b) Ta có: 2014.2019 = 2014.3.673 3 (vì 3 3, theo tính chất) c) Ta có: 1411.2020 = 17.83.2020 17 (vì 17 17, theo tính chất) ♦ Ví dụ 2: Chứng minh rằng (7a)2020 chia hết cho 49 ∀a∈N. ♠ Hướng dẫn – Ta có: (7a)2020 = 72020.a2020 = 72.72018.a2020 = 49.72018.a2020 Vì 49 49 nên 49.72018.a2020 49 ⇒(7a)2020 chia hết cho 49 ∀a∈N. ° Dạng 2: Tìm điều kiện để số a chia hết cho số b * Phương pháp: – Vận dụng các tính chất và dấu hiệu chia hết ♦ Ví dụ 1: Điền vào * để a) b) ♠ Hướng dẫn a) Vận dụng dấu hiệu chia hết để ⇔ (6+*+5) = (11+*) phải chia hết cho 3 ⇒ * ∈ {1;4;7} b) Vận dụng dấu hiệu chia hết để ⇔ (9+*) phải chia hết cho 9 ⇒ * ∈ {0;9} ♦ Ví dụ 2: Tìm chữ số a, b sao cho đồng thời chia hết cho 2,3,5 và 9. ♠ Hướng dẫn – Từ dấu hiệu chia hết ta thấy, 2 và 5 liên quan đến chữ số tận cùng, sau đó ta xét tổng các chữ số phải chia hết cho 9 (vì chia hết cho 9 là chia hết cho 3). – Ta có: và ⇒ chia hết cho 2 và 5 thì b = 0. – Để chia hết cho 3 và 9 ⇒ (a + 6 + 3 + 0) 9 ⇒ a ∈ {0;9} ⇒ a = 9. (vì số 0 đứng đầu không có nghĩa) – Kết luận: a=9; b=0 thì đồng thời chia hết cho 2;3;5;9. ♦ Ví dụ 3: Tìm a để nhưng không chia hết cho 9. ♠ Hướng dẫn – Từ dấu hiệu chia hết cho 3 và chia hết cho 9, ta có: ⇒ (a+2+0+2+0) chia hết cho 3 ⇒ (a+4) chia hết cho 3 ⇒ a = 2 – Kết luận: Với a = 2 thì mà không chia hết cho 9. ° Dạng 3: Chứng minh một biểu thức chia hết cho một số * Phương pháp: – Vận dụng các tính chất tổng chia hết, hiệu chia hết ♦ Ví dụ 1: Chứng minh rằng S = 5 + 52 + 53 +…+ 599 + 5100 chia hết cho 6. ♠ Hướng dẫn – Ta có: S = 5 + 52 + 53 +…+ 599 + 5100 = 5(1+5) + 53(1+5) +…+ 599(1+5) = 6.(5 + 53 + 55 +…+ 599) Vì 6 6 nên S chia hết cho 6 (theo tính chất). ♦ Ví dụ 2: Chứng minh rằng a) 36 + 81 + 171 chia hết cho 9 b) 135 + 275 + 335 chia hết cho 5 c) 2124 – 204 chia hết cho 4 d) 6433 – 2058 chia hết cho 7 ♠ Hướng dẫn a) Ta có: 36 9; 81 9; 171 9 nên (36 + 81 + 171) 9 (theo tính chất chia hết của một tổng) b) Ta có: 135 5; 275 5; 335 5 nên (135 + 275 + 335) 5 (theo tính chất chia hết của một tổng) c) Ta có: 2124 4; 204 4 nên (2124 – 204) 4 (theo tính chất chia hết của một hiệu) d) Ta có: 6433 7; 2058 7 nên (6433 – 2058) 7 (theo tính chất chia hết của một hiệu) ♦ Ví dụ 3: Chứng minh rằng a) A = 1 + 3 + 32 +…+ 311 chia hết cho 40. b) B = 5 + 52 + 53 +…+ 58 chia hết cho 30. ♠ Hướng dẫn a) Ta có: A = 1 + 3 + 32 +…+ 311 = (1 + 3 + 32 + 33) + 34(1 + 3 + 32 + 33) + 38(1 + 3 + 32 + 33) = (1 + 3 + 32 + 33)(1 + 34 + 38) = 40.(1 + 34 + 38) ⇒ A chia hết cho 40. a) Ta có: B = 5 + 52 + 53 +…+ 58 = 5(1 + 5) + 52(5+25) + 54(5+25) + 56(5+25) = 30(1 + 52 + 54 +56). ⇒ B chia hết cho 30. ° Dạng 4: Một số dạng bài toán chứng minh khác * Phương pháp: – Vận dụng các tính chất và dấu hiệu chia hết. ♦ Ví dụ 1: Chứng minh tổng 3 số tự nhiên liên tiếp chia hết cho 3 ♠ Hướng dẫn – Gọi ba số tự nhiên liên tiếp là: a, a+1 và a+2 ⇒ Tổng ba số là: a + a + 1 + a + 2 = (a + a + a) + (1 + 2) = (3a + 3) 3 (theo tính chất chia hết của 1 tổng) ♦ Ví dụ 2: Chứng minh tích của 2 số tự nhiên liên tiếp chia hết cho 2 ♠ Hướng dẫn – Gọi hai số tự nhiên liên tiếp là: b, b+1 ⇒ Tích hai số là: b(b + 1) – Nếu b chẵn thì b=2k (k∈N) ⇒ 2k(2k+1) 2 (do 2k 2) – Nếu b lẻ thì b=2k+1 (k∈N) ⇒ (2k+1)(2k+1+1) = (2k+1)(2k+2) 2 (do (2k + 2) 2) ⇒ Tích của 2 số tự nhiên liên tiếp chia hết cho 2. ♦ Ví dụ 3: Chứng minh tích của 2 số tự nhiên chẵn liên tiếp luôn chia hết cho 8 ♠ Hướng dẫn – Gọi hai số chẵn liên tiếp là: 2a và 2a+2 (a∈N) – Khi đó ta có: 2a.(2a+2) = 4a.(a+1) – Ta thấy, a(a+1) là hai số tự nhiên liên tiếp nên theo ví dụ 2 thì a(a+1) chia hết cho 2. ⇒ 4.a.(a+1) chia hết cho 4.2 ⇒ 4.a.(a+1) chia hết cho 8. – Kết luận: 2a.(2a+2) luôn chia hế cho 8, (∀a∈N). ♦ Ví dụ 4: Chứng minh rằng với mọi số tự nhiên a thì tích (a + 3).(a +6) chia hết cho 2. ♠ Hướng dẫn ◊ Với mọi số tự nhiên a (a chẵn hoặc a lẻ) ta có thể viết: a = 2k hoặc a = 2k + 1 (với k∈N). – Với a = 2k ta có: (a+3)(a+6) = (2k+3)(2k+6) = 2.(2k+3)(k+3) chia hết cho 2. – Với a = 2k + 1 ta có: (a+3).(a+6) = (2k+1 +3).(2k+1+6) = (2k+4).(2k+7) = 2.(k+2).(2k+7) chia hết cho 2. – Vậy với mọi số tự nhiên a thì (a+3)(a+6) chia hết cho 2. Hy vọng với bài viết hệ thống lại các bài toán vận dụng tính chất và dấu hiệu chia hết – toán 6 ở trên hữu ích cho các em. Mọi góp ý và thắc mắc các em vui lòng để lại bình luận dưới bài viết để thầy cô trường Tmdl.edu.vn ghi nhận và hỗ trợ, chúc các em học tập tốt! Đăng bởi: Tmdl.edu.vn Chuyên mục: Giáo Dục
Bản quyền bài viết thuộc trường Trường Trung Cấp Nghề Thương Mại Du Lịch Thanh Hoá. Mọi hành vi sao chép đều là gian lận!
Nguồn chia sẻ: Trường Tmdl.edu.vn (tmdl.edu.vn)
Trang chủ: tmdl.edu.vn
Danh mục bài: Giáo dục
