Các công thức Biến đổi Căn thức bậc hai và Bài tập vận dụng. Trong chương 1 toán lớp 9 nội dung chính các em được học về căn thức bậc hai, bậc 3. Để vận dụng giải được các bài tập về căn thức này điều bắt buộc là chúng ta phải nhớ được các công thức.
Bài viết này, chúng ta cùng ôn lại các công thức biến đổi căn thức bậc hai và vận dụng các công thức này để giải các bài tập minh họa. Việc giải bài tập nhiều sẽ giúp các em hiểu rõ và ghi nhớ tốt hơn các công thức qua đó rèn luyện được các kỹ năng giải toán.
Bạn đang xem bài: Các công thức Biến đổi Căn thức bậc hai và Bài tập vận dụng – Toán lớp 9
I. Các công thức biến đổi căn thức bậc hai cần nhớ.
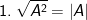
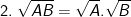 (với A≥0 và B≥0)
(với A≥0 và B≥0)
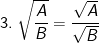 (với A≥0 và B>0)
(với A≥0 và B>0)
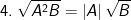 (với B≥0)
(với B≥0)
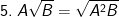 (với A≥0 và B≥0)
(với A≥0 và B≥0)
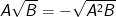 (với A<0 và B≥0)
(với A<0 và B≥0)
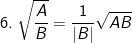 (với AB ≥0 và B≠0)
(với AB ≥0 và B≠0)
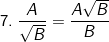 (với B>0)
(với B>0)
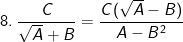 (với A≥0 và A≠B2)
(với A≥0 và A≠B2)
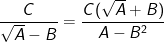 (với A≥0 và A≠B2)
(với A≥0 và A≠B2)
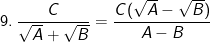 (với A≥0; B≥0 và A≠B)
(với A≥0; B≥0 và A≠B)
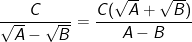 (với A≥0; B≥0 và A≠B)
(với A≥0; B≥0 và A≠B)
Như vậy ở trên là các công thức biến đổi căn thức bậc 2, các em lưu ý rằng: các biểu thức trong căn bậc 2 phải không âm, chính vì vậy mà mỗi công thức trên nếu có các điều kiện đi kèm các em cần phải ghi nhớ để tránh phép biến đổi của mình bị sai.
II. Bài tập vận dụng các phép biến đổi căn thức
* Bài 70 trang 40 SGK Toán 9 Tập 1: Tìm giá trị các biểu thức sau bằng cách biến đổi, rút gọn thích hợp:
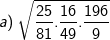
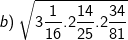
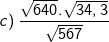
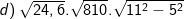
* Lời giải:
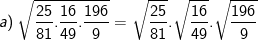
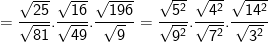
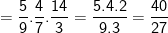
– Ta cũng có thể biến đổi như sau:
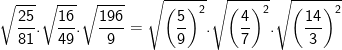
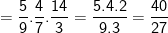
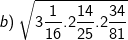
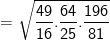
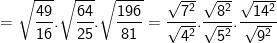
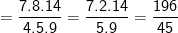
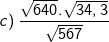
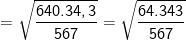
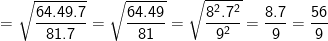
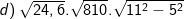
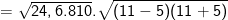
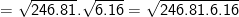
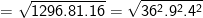
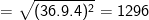
* Bài 71 trang 40 SGK Toán 9 Tập 1: Rút gọn các biểu thức sau:
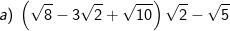
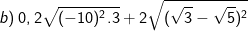
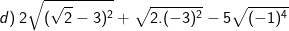
* Lời giải:
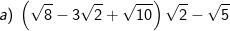
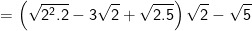
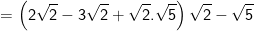
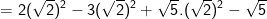
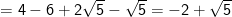
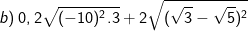
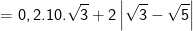
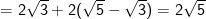
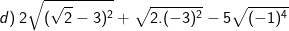
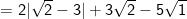
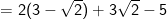
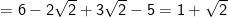
* Bài 73 trang 40 SGK Toán 9 Tập 1: Rút gọn rồi tính giá trị các biểu thức sau:
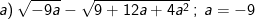
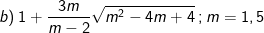
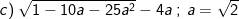
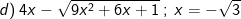
* Lời giải:
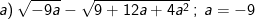
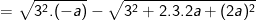
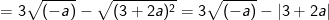
– Tại a = -9 thay vào ta được:
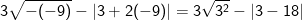
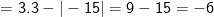
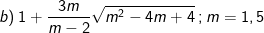
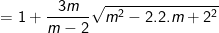
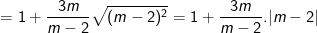
– Tại m = 1,5 thay vào ta được:
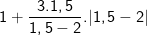
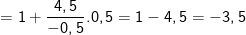
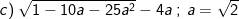
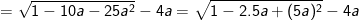
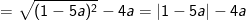
– Tại 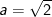 thay vào ta được:
thay vào ta được:
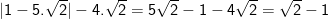
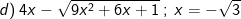
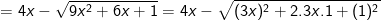
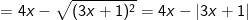
– Tại 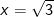 thay vào ta được
thay vào ta được
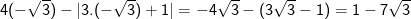
* Bài 74 trang 40 SGK Toán 9 Tập 1: Tìm x, biết:
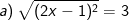
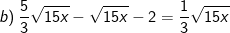
* Lời giải:
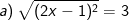
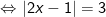 (*)
(*)
+ Nếu 2x – 1 ≥ 0 ⇒ x ≥ 1/2 thì |2x – 1| = 2x – 1 ta có
(*) ⇔ 2x – 1 = 3 ⇔ 2x = 4 ⇔ x = 2 (thỏa điều kiện x≥1/2).
+ Nếu Nếu 2x – 1 < 0 ⇒ x < 1/2 thì |2x – 1| = -(2x – 1) = 1 – 2x ta có
(*) ⇔ 1 – 2x = 3 ⇔ 2x = -2 ⇔ x = -1 (thỏa điều kiện x<1/2).
→ Vậy phương trình có 2 nghiệm: x = 2 và x = -1
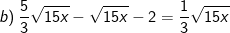 (*)
(*)
– Điều kiện: x≥0.
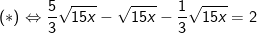
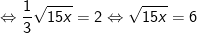
(Bình phương 2 vế của phương trình)
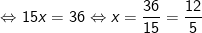
* Bài 76 trang 41 SGK Toán 9 Tập 1: Cho biểu thức
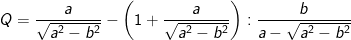 (với a>b>0).
(với a>b>0).
a) Rút gọn Q.
b) Xác định giá trị của Q khi a = 3b.
* Lời giải:
a) Rút gọn Q.
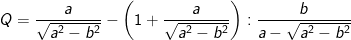
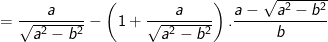
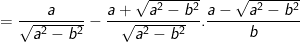
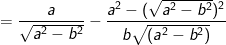
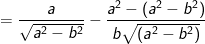
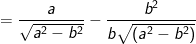
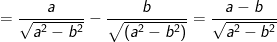
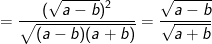
> Lưu ý: ở phép biến đổi trên do giả thiết a>b>0 nên a-b>0 ta mới có thể viết:
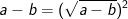 và
và 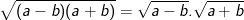
b) Thay a = 3b vào ta được:
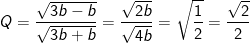
Như vậy việc vận dụng các công thức biến đổi căn thức bậc hai giúp chúng ta giải một số dạng bài tập về rút gọn biểu thức, tính giá trị của biểu thức chứa căn bậc hai một cách dễ dàng hơn.
Cũng cần lưu ý rằng đối với 1 biểu thức khi rút gọn chúng ta có thể vận dụng các phép biến đổi khác nhau, tuy nhiên kết quả rút gọn cuối cùng phải giống nhau.
Bản quyền bài viết thuộc Trường Trung Cấp Nghề Thương Mại Du Lịch Thanh Hoá. Mọi hành vi sao chép đều là gian lận!
Nguồn chia sẻ: https://tmdl.edu.vn/cac-cong-thuc-bien-doi-can-thuc-bac-hai-va-bai-tap-van-dung/
Trang chủ: tmdl.edu.vn
Danh mục bài: Giáo dục