Các dạng toán Phương trình bậc 2 một ẩn, cách giải và tính nhẩm nghiệm nhanh. Sau khi đã làm quen với hệ phương trình bậc nhất 2 ẩn, thì phương trình bậc 2 một ẩn chính là nội dung tiếp theo mà các em sẽ học, đây cũng là nội dung thường có trong chương trình ôn thi vào lớp 10 THPT.
Vì vậy, trong bài viết này chúng ta cùng tìm hiểu cách giải phương trình bậc 2 một ẩn, cách tính nhẩm nghiệm nhanh bằng hệ thức Vi-et, đồng thời giải một số dạng toán về phương trình bậc 2 một ẩn để thông qua bài tập các em sẽ nắm vững nội dung lý thuyết.
Bạn đang xem bài: Các dạng toán Phương trình bậc 2 một ẩn, cách giải và tính nhẩm nghiệm nhanh – Toán lớp 9
I. Tóm tắt lý thuyết về Phương trình bậc 2 một ẩn
1. Phương trình bậc nhất ax + b = 0
– Nếu a ≠ 0, phương trình có nghiệm duy nhất x=(-b/a)
– Nếu a = 0, b ≠ 0, phương trình vô nghiệm
– Nếu a = 0, b = 0, phương trình có vô số nghiệm
2. Phương trình bậc 2: ax2 + bx + c = 0 (a ≠ 0)
a) Công thức nghiệm của phương trình bậc 2 một ẩn:
• Tính 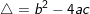
+) Δ > 0: PT có 2 nghiệm: 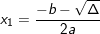 ;
; 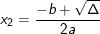
+) Δ = 0: PT có nghiệm kép: 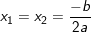
+) Δ < 0: PT vô nghiệm.
• Tính 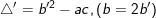
+) Δ’ > 0: PT có 2 nghiệm: 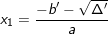 ;
; 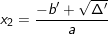
+) Δ’ = 0: PT có nghiệm kép: 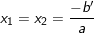
+) Δ’ < 0: PT vô nghiệm.
b) Định lý Vi-et:
– Gọi x1 và x2 là 2 nghiệm của PT bậc 2 một ẩn ax2 + bx + c = 0 (a≠0):
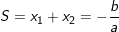 ;
; 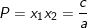
– Ta có thể sử dụng định lý Vi-et để tính các biểu thức của x1 , x2 theo a,b,c:
♦ 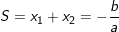
♦ 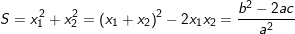
♦ 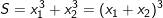
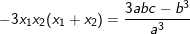
♦ 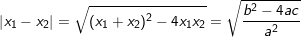
c) Định lý Vi-et đảo:
– Nếu x1 + x2 = S và x1.x2 = P thì x1, x2 là nghiệm của phương trình: X2 – SX + P = 0 (Điều kiện S2 – 4P ≥ 0)
d) Ứng dụng của định lý Vi-et
* Tính nhẩm nghiệm phương trình bậc 2:
– Nếu a + b + c = 0 thì: x1 = 1 và x2 = (c/a);
– Nếu a – b + c = 0 thì: x1 = -1 và x2 = (-c/a);
* Tìm 2 số khi biết tổng và tích
– Cho 2 số x, y, biết x + y = S và x.y = P thì x, y là nghiệm của phương trình: X2 – SX + P = 0
* Phân tích thành nhân tử
– Nếu phương trình: ax2 + bx + c = 0 (a ≠ 0) có 2 nghiệm x1, x2 thì ax2 + bx + c = a(x – x1)(x – x2) = 0
* Xác định dấu của các nghiệm số
– Cho phương trình: ax2 + bx + c = 0 (a ≠ 0), giả sử PT có 2 nghiệm x1, x2 thì S = x1 + x2 = (-b/a); P = x1x2 = (c/a)
– Nếu P < 0 thì phương trình có 2 nghiệm trái dấu
– Nếu P > 0 và Δ > 0 thì phương trình có 2 nghiệm cùng dấu, khi đó nếu S > 0 thì phương trình có 2 nghiệm dương, S < 0 thì phương trình có 2 nghiệm âm.
II. Một số dạng toán phương trình bậc 2 một ẩn
Dạng 1: Giải phương trình bậc 2 một ẩn
* Phương pháp:
+ Trường hợp 1: Phương trình bậc 2 khuyết hạng tử bậc nhất:
– Chuyển hạng tử tự do sang vế phải
– Chia cả 2 vế cho hệ số bậc 2, đưa về dạng x2 = a.
+ Nếu a > 0, phương trình có nghiệm x = ±√a
+ Nếu a = 0, phương trình có nghiệm x = 0
+ Nếu a < 0, phương trình vô nghiệm
+ Trường hợp 2: Phương trình bậc 2 khuyết hạng tử dự do:
– Phân tích vế trái thành nhân tử bằng phương pháp đặt nhân tử chung, đưa về phương trình tích rồi giải.
+ Trường hợp 3: Phương trình bậc 2 đầy đủ:
– Sử dụng công thức nghiệm, hoặc công thức nghiệm thu gọn để giải
– Sử dụng quy tắc tính nhẩm nghiệm để tính nghiệm đối với 1 số phương trình đặc biệt.
Ví dụ: Giải các phương trình sau:
a) 2x2 – 4 = 0 b) x2 + 4x = 0
c) x2 – 5x + 4 = 0
* Lời giải:
a) 2x2 – 4 = 0 ⇔ 2x2 = 4 ⇔ x2 = 2 ⇔ x = ±√2.
⇒ Kết luận: Phương trình có nghiệm x=±√2.
b) x2 + 4x = 0 ⇔ x(x+4) = 0
⇔ x = 0 hoặc x + 4 =0
⇔ x = 0 hoặc x = -4
⇒ Kết luận: Phương trình có nghiệm x=0 và x=-4.
c) x2 – 5x + 4 = 0
* Cách giải 1: sử dụng công thức nghiệm
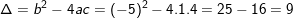
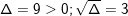
⇒ PT có 2 nghiệm phân biệt: 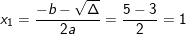 ;
; 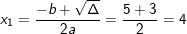
⇒ Kết luận: Phương trình có nghiệm x=1 và x=4.
* Cách giải 2: nhẩm nghiệm
– PT đã cho: x2 – 5x + 4 = 0 có các hệ số a=1; b=-5; c=4 và ta thấy: a + b + c = 1 – 5 + 4 = 0 nên theo ứng dụng của định lý Vi-ét, ta có x1 = 1; x2 = c/a = 4/1 = 4
⇒ Kết luận: Phương trình có nghiệm x=1 và x=4.
* Một số lưu ý khi giải phương trình bậc 2:
♦ Nếu gặp hằng đẳng thức 1 và 2 thì đưa về dạng tổng quát giải bình thường, không cần giải theo công thức, ví dụ: x2 – 2x + 1 = 0 ⇔ (x-1)2 = 0 ⇔ x = 1.
♦ Phải sắp xếp lại đúng thứ tự các hạng tử để lập thành phương trình ax2 + bx + c = 0 rồi mới áp dụng công thức, ví dụ: x(x – 5) = 6 ⇔ x2 – 5x = 6 ⇔ x2 – 5x – 6 = 0 ⇔ áp dụng công thức giải tiếp,…
♦ Không phải lúc nào x cũng là ẩn số mà có thể là ẩn y, ẩn z ẩn t hay ẩn a, ẩn b,… tùy vào cách ta chọn
biến, ví dụ: a2 – 3a + 2 = 0; t2 – 6t + 5 = 0.
Dạng 2: Phương trình đưa về phương trình bậc 2 bằng phương pháp đặt ẩn phụ
a) Phương trình trùng phương: ax4 + bx2 + c = 0 (a≠0)
* Phương pháp:
– Đặt t = x2 (t≥0), đưa PT về dạng: at2 + bt + c = 0
– Giải PT bậc 2 theo t, kiểm tra nghiệm t có thoả điều kiện hay không, nếu có, trở lại phương trình x2 = t để tìm nghiệm x.
b) Phương trình chứa ẩn ở mẫu:
* Phương pháp:
– Tìm điều kiện xác định của phương trình
– Quy đồng mẫu thức 2 vế rồi khử mẫu
– Giải phương trình vừa nhận được
– Kiểm tra điều kiện các giá trị tìm được, loại các giá trị không thoả mãn điều kiện, các giá trị thoả điều kiện xác định là nghiệm của phương trình đã cho.
Ví dụ: Giải phương trình sau:
a) x4 – 3x2 + 2 = 0
b) 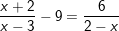
* Lời giải:
a) x4 – 3x2 + 2 = 0 (*)
– Đặt t = x2 (t ≥ 0) ta có (*) ⇔ t2 – 3t + 2 = 0
– Ta thấy a + b + c = 0 ⇒ t = 1 hoặc t = 2 (đều thoả ĐK t ≥ 0)
– Với t = 1: x2 = 1 ⇒ x = ±1
– Với t = 2: x2 = 2 ⇒ x = ±√2
⇒ Kết luận: Phương tình có nghiệm (-√2; -1; 1; √2)
b) 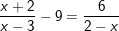 (*)
(*)
ĐK: x ≠ 3; x ≠ 2
– Quy đồng khử mẫu, PT (*) ta được:
(x+2)(2-x) – 9(x-3)(2-x) = 6(x-3)
⇔ 4 – x2 – 9(-x2 + 5x – 6) = 6x – 18
⇔ 4 – x2 + 9x2 -45x + 54 – 6x + 18 = 0
⇔ 8x2 – 51x + 76 = 0
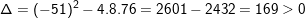 ,
, 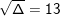
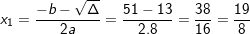 ;
;
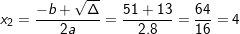
– Cả 2 nghiệm trên đều thoả ĐK x ≠ 3; x ≠ 2;
⇒ PT có nghiệm: x1 = 19/8 và x2 = 4;
Dạng 3: Giải biện luận số nghiệm của phương trình bậc 2 có tham số
* Phương pháp:
– Sử dụng công thức nghiệm, hoặc công thức nghiệm thu gọn để giải,
– Tính 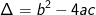 theo tham số:
theo tham số:
+ Nếu Δ > 0: phương trình có 2 nghiệm phân biệt
+ Nếu Δ = 0: phương trình có nghiệm kép
+ Nếu Δ < 0: phương trình vô nghiệm
Ví dụ: Giải biện luận theo m, phương trình: mx2 – 5x – m – 5 = 0 (*)
* Lời giải:
– Trường hợp m = 0 thì (*) trở thành: -5x – 5 = 0 ⇒ x = -1
– Trường hợp m ≠ 0, ta có:
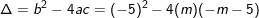
= 25 + 4m(m+5) = 25 + 4m2 + 20m = (2m+5)2
– Ta thấy: Δ = (2m+5)2 ≥ 0, ∀ m nên PT(*) sẽ luôn có nghiệm
+ Nếu Δ = 0 ⇒ m =-5/2 thì PT (*) có nghiệp duy nhất: 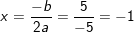
+ Nếu Δ = 0 ⇒ m < -5/2 hoặc m > -5/2 thì PT (*) có 2 nghiệm phân biệt:
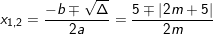
Dạng 4: Xác định tham số m để phương trình bậc 2 thoả mãn điều kiện nghiệm số
* Phương pháp
– Giải phương trình bậc 2, tìm x1; x2 (nếu có)
– Với điều kiện về nghiệm số của đề bài giải tìm m
– Bảng xét dấu nghiệm của phương trình bậc 2 một ẩn:
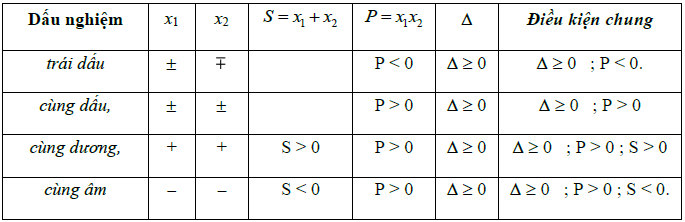
* Lưu ý: Nếu bài toán yêu cầu phương trình có 2 nghiệm phân biệt thì ta xét Δ > 0 ; còn nếu đề bài chỉ nói chung chung phương trình có 2 nghiệm thì ta xét Δ ≥ 0.
• Tìm điều kiện tổng quát để phương trình ax2 + bx + c = 0 (a≠0) có:
1. Có nghiệm (có hai nghiệm) ⇔ Δ ≥ 0
2. Vô nghiệm ⇔ Δ < 0
3. Nghiệm duy nhất (nghiệm kép, hai nghiệm bằng nhau) ⇔ Δ = 0
4. Có hai nghiệm phân biệt (khác nhau) ⇔ Δ > 0
5. Hai nghiệm cùng dấu ⇔ Δ ≥ 0 và P > 0
6. Hai nghiệm trái dấu ⇔ Δ > 0 và P < 0 ⇔ a.c < 0
7. Hai nghiệm dương (lớn hơn 0) ⇔ Δ ≥ 0; S > 0 và P > 0
8. Hai nghiệm âm (nhỏ hơn 0) ⇔ Δ ≥ 0; S < 0 và P > 0
9. Hai nghiệm đối nhau ⇔ Δ ≥ 0 và S = 0
10.Hai nghiệm nghịch đảo nhau ⇔ Δ ≥ 0 và P = 1
11. Hai nghiệm trái dấu và nghiệm âm có giá trị tuyệt đối lớn hơn ⇔ a.c < 0 và S < 0
12. Hai nghiệm trái dấu và nghiệm dương có giá trị tuyệt đối lớn hơn ⇔ a.c < 0 và S > 0
Ví dụ: Cho phương trình bậc 2 ẩn x tham số m: x2 + mx + m + 3 = 0 (*)
a) Giải phương trình với m = -2.
b) Tìm m để phương trình có 2 nghiệm x1 , x2 thoả x12 + x22 = 9
c) Tìm m để phương trình có 2 nghiệm x1 , x2 thoả 2x1 + 3x2 = 5
* Lời giải:
a) với m = -2 thì (*) ⇔ x2 – 2x + 1 = 0
– Ta thấy, a + b + c = 0 nên theo Vi-et PT có nghiệm: x1 = 1; x2 = c/a = 1;
– Hoặc: x2 – 2x + 1 = 0 ⇔ (x-1)2 = 0 nên có nghiệp kép: x = 1
b) Để PT: x2 + mx + m + 3 = 0 có 2 nghiệm thì:
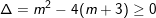
– Khi đó theo định lý Vi-et ta có: x1 + x2 = -m và x1x2 = m+3
Mà x12 + x22 = x12 + 2x1x2 + x22 – 2x1x2
= (x1 + x2)2 – 2x1x2 = (-m)2 – 2(m+3) = m2 – 2m – 6
– Do đó, để: x12 + x22 = 9 ⇔ m2 – 2m – 6 = 9 ⇔ m2 – 2m – 15 = 0
Ta tính Δ’m = (-1)2 – 1(-15) = 16 ⇒ 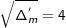
⇒ PT có 2 nghiệm m1 = (1+4)/1 = 5 và m2 = (1-4)/1 = -3
– Thử lại ĐK của m để Δ ≥ 0:
_ Với m = 5 ⇒ Δ = 25 – 32 = -7 < 0 (loại)
_ Với m = -3 ⇒ Δ = 9 > 0 (thoả ĐK)
⇒ Vậy với m = -3 thì PT (*) có 2 nghiệm thoả x12 + x22 = 9
c) Theo câu b) PT có 2 nghiệm x1 , x2 ⇔ Δ ≥ 0
Theo Vi-et ta có: 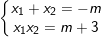
– Theo yêu cầu bài toán ta cần tìm m sao cho: 2x1 + 3x2 = 5, ta sẽ tìm x1 và x2 theo m
– Ta giải hệ: 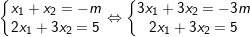
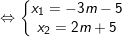
– Lại có x1x2 = m + 3 ⇒ (-3m-5)(2m+5) = m+3
⇔ -6m2 – 25m – 25 = m + 3
⇔ 6m2 + 26m + 28 = 0
⇔ 3m2 + 13m + 14 = 0
Tính Δm = 132 – 4.3.14 = 1 > 0.
⇒ PT có 2 nghiệm phân biệt: m1 = -7/3; m2 = -2
– Thử lại điều kiện: Δ ≥ 0;
_ Với m = -7/3; Δ = 25/9 > 0 (thoả)
_ Với m = -2; Δ = 0 (thoả)
⇒ Kết luận: với m=-2 hoặc m=-7/3 thì PT có 2 nghiệm thoả 2x1 + 3x2 = 5.
Dạng 5: Giải bài toán bằng cách lập phương trình
* Phương pháp: Vận dụng linh hoạt theo yêu cầu bài toán để lập phương trình và giải
Ví dụ: Trong lúc học nhóm Hùng yêu cầu bạn Minh và bạn Lan mỗi người chọn một số, sao cho 2 số này hơn kém nhau là 5 và tích của chúng phải bằng 150, vậy 2 bạn Minh và Lan phải chọn nhưng số nào?
* Lời giải:
– Gọi số bạn Minh chọn là x, thì số bạn Lan chọn sẽ là x + 5
– Theo bài ra, tích của 2 số này là 150 nên ta có: x(x+5) = 150
⇔ x2 + 5x – 150 = 0
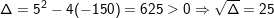
– Phương trình có nghiệm x1 = 10; x2 = -15
– Vậy có 2 cặp số thỏa là: (10; 15) và (-15; -10)
III. Bài tập Phương trình bậc 2 một ẩn
Bài 12 trang 42 sgk toán 9 tập 2: Giải các phương trình sau:
a) x2 – 8 = 0 b) 5x2 – 20 = 0 c) 0,4x2 + 1 = 0
d) 2x2 + x√2 = 0 e) -0,4x2 + 1,2x = 0
* Lời giải Bài 12 trang 42 sgk toán 9 tập 2:
a) x2 – 8 = 0 ⇔ x2 = 8 ⇔ x = ±2√2
b) 5x2 – 20 = 0 ⇔ x2 = 4 ⇔ x = ±2
c) 0,4x2 + 1 = 0 ⇔ x2 = -2,5 ⇔ PT vô nghiệm
d) 2x2 + x√2 = 0 ⇔ x√2.(x√2 +1) = 0 ⇔ x = 0 hoặc x = -1/√2
e) -0,4x2 + 1,2x = 0 ⇔ 0,4x(-x+3) = 0 ⇔ x = 0 hoặc x = 3
Bài 16 trang 45 sgk toán 9 tập 2: Dùng công thức nghiệm giải các phương trình sau
a) 2x2 – 7x + 3 = 0 b) 6x2 + x + 5 = 0
c) 6x2 + x – 5 = 0 d) 3x2 + 5x + 2 = 0
e) y2 – 8y + 16 =0 f) 16z2 + 24z + 9 = 0
* Lời giải Bài 16 trang 45 sgk toán 9 tập 2:
a) 2x2 – 7x + 3 = 0
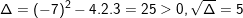
– Phương trình có 2 nghiệm phân biệt:
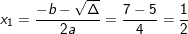 ;
; 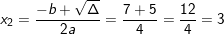
b) PT vô nghiệm
c) x1 = -1; x2 = 5/6
d) x1 = -1; x2 = -2/3
e) nghiệm kép: y = 4
f) nghiệm kép: z = -3/4
III. Luyện tập các dạng bài tập phương trình bậc hai một ẩn
Bài 1: Giải các phương trình sau:
a) 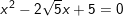
b) 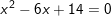
c) 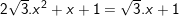
d) 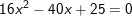
e) 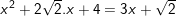
Bài 2: Giải các phương trình sau bằng phương pháp tính nhẩm nghiệm
a) 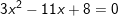
b) 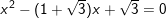
c) 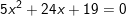
d) 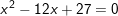
e) 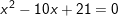
f) 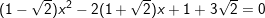
Bài 3: Gọi x1 và x2 là nghiệm của phương trình x2 – 3x – 7 = 0. Không giải phương trình tính giá trị của các biểu thức sau:
1) 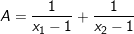
2) 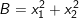
3) 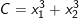
4) 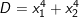
5) 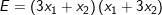
Bài 4: Gọi x1 và x2 là nghiệm của phương trình 3x2 + 5x – 6 = 0. Không giải phương trình tính giá trị của các biểu thức sau:
1) 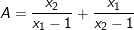
2) 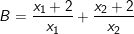
Bài 5: Cho phương trình (2m-1)x2 – 2mx + 1 = 0. Xác định m để phương trình trên có nghiệm thuộc khoảng (-1;0)
Bài 6: Cho phương trình có ẩn x: x2 – mx + m – 1 = 0 (m là tham số).
1) CMR luôn có nghiệm x1, x2 với mọi giá trị của m
2) Đặt 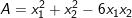
a) Chứng minh: A = m2 – 8m + 8
b) Tìm m sao cho A = 8.
c) Tính giá trị nhỏ nhất của A và của m tương ứng
d) Tìm m sao cho x1 = 3x2.
Hy vọng với bài viết hướng dẫn cách giải phương trình bậc 2 một ẩn và các dạng toán cùng cách tính nhẩm nghiệm ở trên hữu ích cho các em. Mọi góp ý và thắc mắc các em vui lòng để lại lời nhắn dưới phần bình luận để thầy cô trường THPT Thành phố Sóc Trăng ghi nhận và hỗ trợ, chúc các em học tập tốt.
Bản quyền bài viết thuộc trường Trường Trung Cấp Nghề Thương Mại Du Lịch Thanh Hoá. Mọi hành vi sao chép đều là gian lận!
Nguồn chia sẻ: Trường Tmdl.edu.vn (tmdl.edu.vn)
Trang chủ: tmdl.edu.vn
Danh mục bài: Giáo dục