
Tín hiệu của toán học bạn cần biết?
Bạn đang xem bài: Các dấu trong toán học bạn cần biết?
Trong toán học, có rất nhiều ký hiệu đặc thù như dấu ngoặc nhọn, dấu ngoặc nhọn, dấu ngoặc nhọn, dấu ngoặc nhọn. Tôi ko biết sử dụng nó lúc nào và ở đâu.Vì vậy tôi sẽ tóm tắt lại bài viết này Ký hiệu toán học Hãy cho bạn hữu của bạn biết.
1. Bảng ký hiệu các ký hiệu toán học
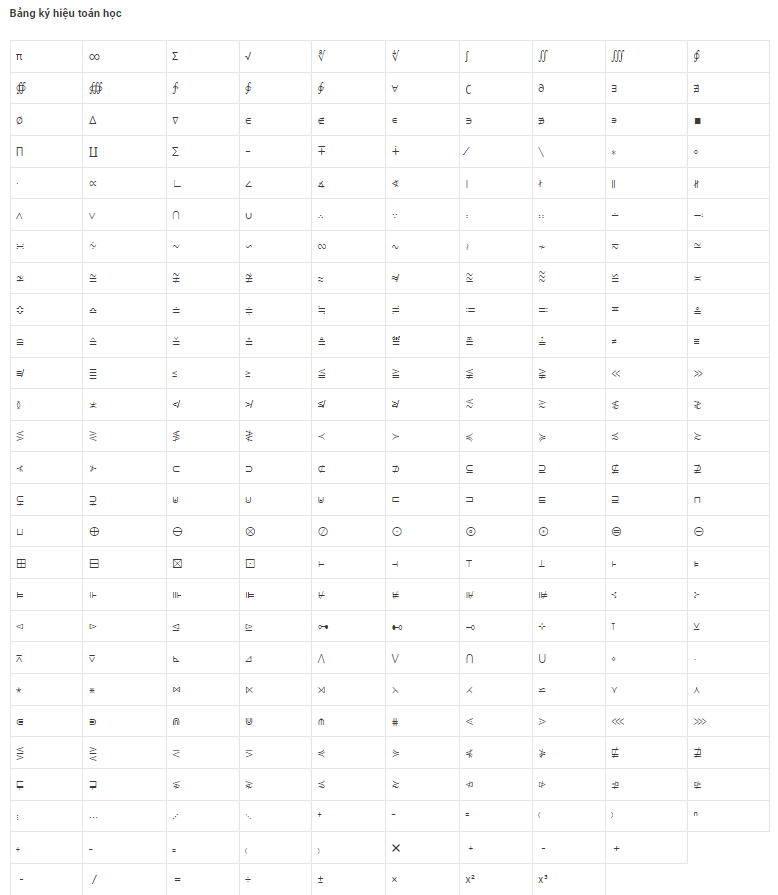
Như bảng kí hiệu hóa học ở trên, mình sẽ tổng hợp lại một số kí hiệu và kí hiệu toán học cho các bạn:
| biểu tượng | Nội dung |
| + | Thêm dấu: Thường được gọi là dấu cộng hoặc dấu cộng |
| – – | Dấu trừ: Đôi lúc được gọi là dấu trừ |
| NS | Biểu tượng nhân: Thường được gọi là dấu thời kì hoặc dấu thời kì |
| ÷ | Tín hiệu chia: chia |
| = | dấu bằng |
| | | Giá trị tuyệt đối |
| ≠ | Không công bình |
| () | dấu ngoặc |
| [] | Dấu ngoặc vuông |
| % | Dấu phần trăm: 100 trở lên |
| Σ | Ký hiệu tổng lớn: tổng |
| √ | Dấu căn bậc hai |
| Tín hiệu bất đồng đẳng: nhỏ | |
| >> >> | Tín hiệu của sự bất đồng đẳng: lớn hơn |
| !! | yếu tố |
| θ | Theta |
| π | Số pi |
| ≅ | Về |
| ∅ | bộ trống |
| ∠ | Dấu góc |
| !! | Tín hiệu giai thừa |
| ∴ | vì thế |
| ∞ | Infiniti |
Dưới đây là danh sách đầy đủ 24 chữ cái Hy Lạp thường được sử dụng trong toán học, vật lý và hóa học.Và cách đọc các ký hiệu toán học
- α (alpha)
- β (beta)
- (gamma)
- (đồng bằng)
- (Epsilon)
- (Zeta)
- (Eta)
- (Theta)
- (Jota)
- (Kappa)
- Lambda (Lambda)
- μ (Mu)
- (Nu)
- (Xi)
- (Omicron)
- (Số pi)
- (Thấp)
- (sigma)
- (vận tải)
- (Upsilon)
- (Châu phi)
- (chi trả)
- (Tê ngưu)
- (omega)
2. Dấu ngoặc đơn trong toán học có tức là gì?
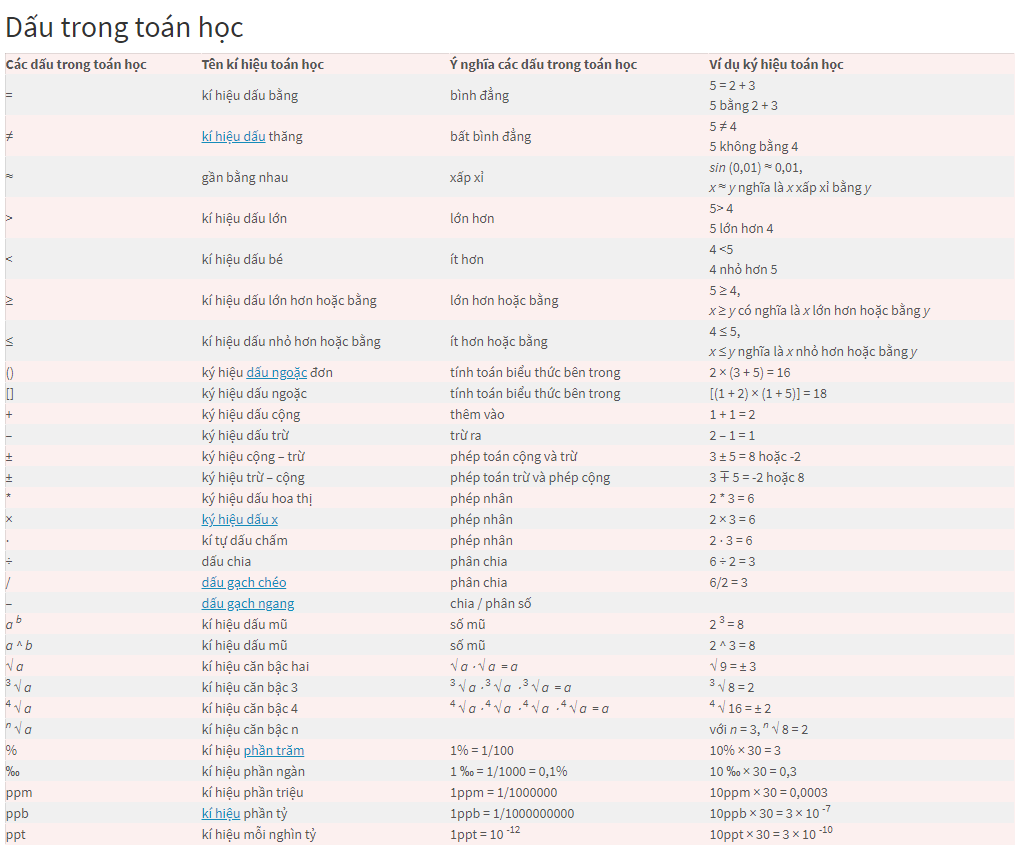
* Sử dụng dấu ngoặc đơn ()
Dấu ngoặc đơn được sử dụng để nhóm các số và / hoặc các biến. Nếu bạn gặp sự cố bao gồm dấu ngoặc vuông, bạn nên sử dụng trật tự các thao tác để khắc phục sự cố. Ví dụ, nó giải bài toán sau: 9 – 5 (8 – 3) x 2 + 6
Đối với vấn đề này, trước tiên bạn cần tính toán hoạt động được đặt trong dấu ngoặc đơn. Đây thường là một phép toán thậm chí theo sau phép toán khác được nhắc đến. Trong bài toán này, các phép tính nhân và chia thông thường được thực hiện trước phép trừ (phép trừ), nhưng 8-3 được đặt trong dấu ngoặc đơn, vì vậy chúng ta sẽ khắc phục phần này của bài toán trước. Sau lúc xử lý các phép tính trong ngoặc đơn, hãy bỏ qua chúng. Trong trường hợp này, (8 – 3) trở thành 5, khắc phục vấn đề sau.
9 – 5 (8 – 3) x 2 + 6
= 9 – 5 ÷ 5 x 2 + 6
= 9 – 1 x 2 + 6
= 9 – 2 + 6
= 7 + 6
= 13
Xem xét rằng theo trật tự của các phép toán, trước tiên hãy tính trị giá trong dấu ngoặc đơn, sau đó sử dụng số mũ để tính số, sau đó nhân và / hoặc chia, và cuối cùng là cộng hoặc trừ. Nhân và chia, cộng và trừ giữ nguyên vị trí theo trật tự của các phép toán, vì vậy các phép toán này được thực hiện từ trái sang phải.
Trong bài toán trên, sau lúc thực hiện phép trừ trong ngoặc vuông, trước hết bạn cần chia 5 cho 5 để được 1. Sau đó nhân 1 với 2 để được 2. Sau đó trừ 2 đi 9 để được 7. Sau đó thêm 7 và 6 và câu trả lời cuối cùng là 13.
* Dấu ngoặc đơn cũng có thể có tức là phép nhân
Bài toán: Trong 3 (2 + 5), dấu ngoặc đơn biểu thị phép nhân. Tuy nhiên, phép nhân ko diễn ra cho tới lúc hoàn thành phép toán trong ngoặc (2 + 5), vì vậy bạn cần giải các bài toán sau:
3 (2 + 5)
= 3 (7)
= 21
* Ví dụ về dấu ngoặc []
Dấu ngoặc đơn được sử dụng sau dấu ngoặc đơn để nhóm các số và biến. Thông thường, bạn sử dụng dấu ngoặc đơn trước tiên, sau đó là dấu ngoặc vuông, sau đó là dấu ngoặc nhọn. Sau đây là một ví dụ về vấn đề với dấu ngoặc vuông.
4-3 [4 – 2 (6 – 3)] 3
= 4 – 3 [4 – 2 (3)] ÷ 3 (Thực hiện thao tác đặt trong dấu ngoặc đơn trước. Bỏ dấu ngoặc đơn.)
= 4 – 3 [4 – 6] ÷ 3 (Thực hiện thao tác trong ngoặc đơn.)
= 4 – 3 [-2] ÷ 3 (dấu ngoặc đơn cho biết số trong đó được nhân với -3 x -2.)
= 4 + 6 3
= 4 + 2
= 6
* Ví dụ về dấu ngoặc nhọn {}
Dấu ngoặc nhọn cũng được sử dụng để nhóm các số và biến. Vấn đề trong ví dụ này sử dụng dấu ngoặc đơn, dấu ngoặc nhọn và dấu ngoặc nhọn. Các dấu ngoặc bên trong các dấu ngoặc khác (hoặc dấu ngoặc nhọn và ngoặc nhọn) còn được gọi là “dấu ngoặc đơn lồng nhau”. Hãy nhớ luôn làm việc từ trong ra ngoài nếu có dấu ngoặc đơn bên trong dấu ngoặc nhọn và dấu ngoặc nhọn hoặc dấu ngoặc nhọn lồng nhau.
2 {1 + [4 (2 + 1) + 3]}
= 2 {1 + [4 (3) + 3]}
= 2 {1 + [12 + 3]}
= 2 {1 + [15]}
= 2 {16}
= 32
* Ghi chú về dấu ngoặc đơn, dấu ngoặc đơn, dấu ngoặc đơn
Dấu ngoặc nhọn, dấu ngoặc nhọn và dấu ngoặc nhọn đôi lúc được gọi tương ứng là “hình tròn”, “hình vuông” và “dấu ngoặc nhọn”. Dấu ngoặc nhọn cũng được sử dụng theo bộ như sau:
{2, 3, 6, 8, 10 …}
Khi sử dụng dấu ngoặc vuông lồng nhau, trật tự luôn là dấu ngoặc đơn, dấu ngoặc nhọn và dấu ngoặc nhọn. (Trích: Loigiaihay)
Một số bài viết liên quan tới “Học thuật”:
Xem thêm các bài viết mới: gì ?
..
Thông tin thêm
Các dấu trong toán học bạn cần biết?
[rule_3_plain]
Các tín hiệu trong toán học bạn cần biết?
Trong toán học, sẽ có rất nhiều ký hiệu đặc thù như dấu ngoặc nhọn, dấu ngoặc nhọn, dấu ngoặc nhọn, dấu ngoặc nhọn,… Và chúng ta sẽ ko biết sử dụng nó lúc nào và ở đâu! Vì vậy bài viết này mình sẽ tổng hợp lại tín hiệu trong toán học cho bạn hữu của bạn biết.
1. Bảng kí hiệu các tín hiệu trong toán học
Như bảng kí hiệu hóa học ở trên, mình sẽ tổng hợp một số kí hiệu và kí hiệu trong toán học cho các bạn:
Biểu tượng
Nội dung
+
Thêm dấu: Thường được gọi là dấu cộng hoặc dấu cộng
–
Dấu trừ: Thường được gọi là dấu trừ
NS
Dấu nhân: Thường được gọi là dấu thời kì hoặc dấu thời kì
÷
Tín hiệu của sự phân chia: Để phân chia
=
Dấu bằng
| |
Giá trị tuyệt đối
≠
Không bằng
()
Dấu ngoặc đơn
[]
Dấu ngoặc vuông
%
Dấu phần trăm: Trên 100
Σ
Tín hiệu tổng lớn: Sum
√
Dấu căn bậc hai
Tín hiệu bất đồng đẳng: Nhỏ hơn
>
Tín hiệu bất đồng đẳng: Lớn hơn
!
yếu tố
θ
Theta
π
Số Pi
≅
Khoảng
∅
Bộ trống
∠
Dấu góc
!
Tín hiệu giai thừa
∴
vì thế
∞
vô cực
Dưới đây là danh sách đầy đủ 24 chữ cái trong bảng chữ cái Hy Lạp thường được sử dụng trong Toán, Lý và Hóa. và cách đọc các ký hiệu toán học
α (Alpha)
β (Beta)
(Gamma)
(Đồng bằng)
(Epsilon)
(Zeta)
(Eta)
(Theta)
(Iota)
(Kappa)
Lambda (Lambda)
μ (Mu)
(Nu)
(Xi)
(Omicron)
(Số Pi)
(Rho)
(Sigma)
(Tàu)
(Upsilon)
(Châu phi)
(Chi)
(Psi)
(Omega)
2. Ý nghĩa của dấu ngoặc trong toán học?
* Sử dụng dấu ngoặc đơn ()
Dấu ngoặc đơn được sử dụng để nhóm các số hoặc biến hoặc cả hai. Khi bạn thấy một vấn đề có chứa dấu ngoặc, bạn cần sử dụng trật tự các phép toán để khắc phục vấn đề đó. Ví dụ, giải bài toán: 9 – 5 (8 – 3) x 2 + 6
Đối với vấn đề này, trước tiên bạn phải tính toán hoạt động trong dấu ngoặc đơn – ngay cả lúc đó là một phép toán thường xuất hiện sau các phép toán khác trong bài toán. Trong bài toán này, các phép tính nhân và chia thông thường sẽ đứng trước phép trừ (phép trừ), tuy nhiên, vì 8 – 3 được đặt trong dấu ngoặc đơn nên bạn giải phần này của bài toán trước. Khi bạn đã quan tâm tới phép tính trong dấu ngoặc đơn, bạn sẽ loại trừ chúng. Trong trường hợp này (8 – 3) trở thành 5, vì vậy bạn sẽ khắc phục vấn đề như sau:
9 – 5 (8 – 3) x 2 + 6
= 9 – 5 ÷ 5 x 2 + 6
= 9 – 1 x 2 + 6
= 9 – 2 + 6
= 7 + 6
= 13
Xem xét rằng theo trật tự của các phép toán, bạn sẽ tính toán những gì trong dấu ngoặc đơn trước tiên, tiếp theo, tính các số với số mũ, sau đó nhân và / hoặc chia, và cuối cùng, cộng hoặc trừ. Nhân và chia, cũng như cộng và trừ, giữ một vị trí ngang nhau trong trật tự các phép toán, vì vậy bạn thực hiện các phép toán này từ trái sang phải.
Trong bài toán trên, sau lúc thực hiện phép trừ trong ngoặc, trước hết bạn cần chia 5 cho 5, được 1; rồi nhân 1 với 2, được 2; rồi trừ 2 với 9, được 7; và sau đó thêm 7 và 6, dẫn tới câu trả lời cuối cùng là 13.
* Dấu ngoặc đơn cũng có thể có tức là phép nhân
Trong bài toán: 3 (2 + 5), dấu ngoặc đơn cho bạn biết phép nhân. Tuy nhiên, bạn sẽ ko nhân cho tới lúc hoàn thành thao tác bên trong dấu ngoặc đơn – 2 + 5 – vì vậy bạn sẽ khắc phục được vấn đề như sau:
3 (2 + 5)
= 3 (7)
= 21
* Ví dụ về Dấu ngoặc []
Dấu ngoặc đơn được sử dụng sau dấu ngoặc đơn để nhóm các số và biến. Thông thường, bạn sẽ sử dụng dấu ngoặc đơn trước tiên, sau đó là dấu ngoặc vuông, tiếp theo là dấu ngoặc nhọn. Dưới đây là một ví dụ về sự cố lúc sử dụng dấu ngoặc:
4 – 3 [4 – 2 (6 – 3)] 3
= 4 – 3 [4 – 2 (3)] ÷ 3 (Thực hiện thao tác trong dấu ngoặc đơn trước; bỏ dấu ngoặc đơn.)
= 4 – 3 [4 – 6] ÷ 3 (Thực hiện thao tác trong ngoặc.)
= 4 – 3 [-2] ÷ 3 (Dấu ngoặc cho biết bạn nhân số trong đó, là -3 x -2.)
= 4 + 6 3
= 4 + 2
= 6
* Ví dụ về dấu ngoặc nhọn {}
Dấu ngoặc nhọn cũng được sử dụng để nhóm các số và biến. Bài toán ví dụ này sử dụng dấu ngoặc đơn, dấu ngoặc nhọn và dấu ngoặc nhọn. Các dấu ngoặc bên trong các dấu ngoặc đơn khác (hoặc dấu ngoặc nhọn và ngoặc nhọn) cũng được gọi là “dấu ngoặc đơn lồng nhau.” Hãy nhớ rằng, lúc bạn có dấu ngoặc đơn bên trong dấu ngoặc nhọn và dấu ngoặc nhọn hoặc dấu ngoặc đơn lồng nhau, hãy luôn làm việc từ trong ra ngoài:
2 {1 + [4 (2 + 1) + 3]}
= 2 {1 + [4 (3) + 3]}
= 2 {1 + [12 + 3]}
= 2 {1 + [15]}
= 2 {16}
= 32
* Ghi chú về Dấu ngoặc đơn, Dấu ngoặc đơn và Dấu ngoặc
Dấu ngoặc đơn, dấu ngoặc nhọn và dấu ngoặc nhọn đôi lúc được gọi tương ứng là dấu ngoặc vuông “tròn”, “vuông” và “xoăn”. Dấu ngoặc nhọn cũng được sử dụng theo bộ, như trong:
{2, 3, 6, 8, 10…}
Khi làm việc với các dấu ngoặc lồng nhau, trật tự sẽ luôn là dấu ngoặc đơn, dấu ngoặc nhọn và dấu ngoặc nhọn. (Trích: Loigiaihay)
Một số bài viết liên quan tới “học thuật” :
Xem thêm nhiều bài mới tại : Là Gì ?
TagsLà gì?
[rule_2_plain]
#Các #dấu #trong #toán #học #bạn #cần #biết
- Tổng hợp: Thư Viện Hỏi Đáp
- Nguồn: https://bigdata-vn.com/cac-dau-trong-toan-hoc-ban-can-biet/
Trang chủ: tmdl.edu.vn
Danh mục bài: Tổng hợp


