Cách chứng minh hình thang cân nhanh nhất và bài tập vận dụng

Cách chứng minh hình thang cân nhanh nhất và bài tập vận dụng

Chuyên đề về hình thang cũng như cách chứng minh hình thang cân học sinh đã được tìm hiểu trong chương trình Toán 8, phân môn Hình học. Đây là phần kiến thức quan trọng của chương trình. Nhằm giúp các bạn nắm chắc hơn về chuyên đề này cũng như thông thạo cách chứng minh hình thang cân, Trường Trung Cấp Nghề Thương Mại Du Lịch Thanh Hoá.vn đã chia sẻ bài viết sau đây. 

I. LÝ THUYẾT VỀ HÌNH THANG CÂN

Bạn đang xem bài: Cách chứng minh hình thang cân nhanh nhất và bài tập vận dụng

1. Định nghĩa

Hình thang cân là hình thang có hai góc kề một đáy bằng nhau.

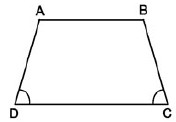
Tứ giác ABCD là hình thang cân (đáy AB; CD)

⇔AB//CD”>⇔AB//CD và Góc C = Góc D

2. Tính chất

– Tính chất 1: Trong một hình thang cân, hai cạnh bên bằng nhau.

Ví dụ: ABCD là hình thang cân (AB // CD)

=> AD = BC

– Tính chất 2: Trong một hình thang cân, hai đường chéo bằng nhau.

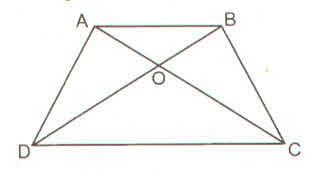
Ví dụ: Cho ABCD là hình thang cân (AB // CD)

=> AC = BD

– Tính chất 3: Hình thang cân luôn nội tiếp được trong một đường tròn.

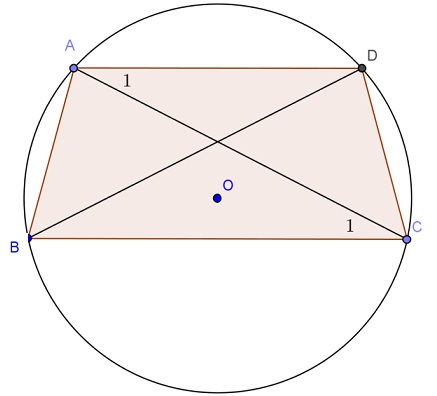
Ví dụ: ABCD là hình thang cân (AB // CD)

=> Luôn có một đường tròn tâm O nội tiếp hình thang này

3. Dấu hiệu nhận biết hình thang cân

1. Hình thang có hai góc kề một đáy bằng nhau là hình thang cân.
2. Hình thang có hai đường chéo bằng nhau là hình thang cân.

Lưu ý:

Hình thang cân thì có 2 cạnh bên bằng nhau nhưng hình thang có 2 cạnh bên bằng nhau chưa chắc là hình thang cân. Ví dụ như hình vẽ dưới đây:

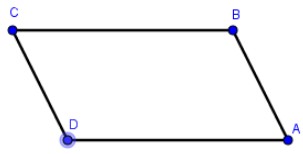
Ví dụ:

+ ABCDABCD là hình thang cân thì AD=BC;AC=BDAD=BC;AC=BD

+ Tứ giác ABCDABCD có {AB//CDˆD=ˆC⇔ABCD{AB//CDD^=C^⇔ABCD là hình thang cân.

+ Tứ giác ABCDABCD có {AB//CDˆA=ˆB⇔ABCD{AB//CDA^=B^⇔ABCD là hình thang cân.

+ Tứ giác ABCDABCD có {AB//CDAC=BD⇔ABCD{AB//CDAC=BD⇔ABCD là hình thang cân.

II. CÁCH CHỨNG MINH HÌNH THANG CÂN

1. Phương pháp chứng minh

Phương pháp 1:

Để chứng minh tứ giác đó là hình thang cân ta phải chứng minh tứ giác đó có 2 cạnh song song với nhau dựa vào các cách chứng minh song song như sau:

• Hai góc đồng vị bằng nhau.
• Hai góc so le trong bằng nhau.
• Hai góc trong cùng phía bù nhau hoặc định lý từ góc vuông đến góc song song.

Phương pháp 2:

Chứng minh hình thang đó có hai góc kề một cạnh đáy bằng nhau thì hình thang đó là hình thang cân.

Phương pháp 3:

Chứng minh hình thang đó có hai đường chéo bằng nhau thì hình thang đó là hình thang cân.

Đây là 3 phương pháp rất hay được sử dụng để các em có thể sử đụng để làm bài tập về chứng minh hình thang cân.

Cách chứng minh một tứ giác là hình thang cân?

• Chứng minh tứ giác đó là hình thang ⇒ Chứng minh tứ giác đó có 2 cạnh song song với nhau ⇒ dựa vào các cách chứng minh song song như: hai góc đồng vị bằng nhau, hai góc so le trong bằng nhau, hai góc trong cùng phía bù nhau hoặc định lý từ góc vuông đến góc song song
• Chứng minh hình thang là hình thang cân theo hai cách ở trên

2. Một số ví dụ về cách chứng minh hình thang cân

Ví dụ 1:

Cho hình thang cân ABCD có AB||CD, AB<CD, AB=2cm, DC=4cm. Từ A,B lần lượt kẻ đường cao xuống DC tại H,K sao cho AH⊥DC, BK⊥DC. Chứng minh rằng DH=KC?

Lời giải:

Xét hai tam vuông AHD và tam giác vuông BKD ta có:

AD=BC, góc ADH =  góc KCB (Theo giả thiết đề bài)

• → ⊿AHD = ⊿BKD ( theo trường hợp cạnh huyền-góc nhọn)
• → DH=KC (đpcm)

 Ví dụ 2:

Trong các tứ giác ABCD, EFGH trên giấy kẻ ô vuông (h.31), tứ giác nào là hình thang cân? Vì sao?

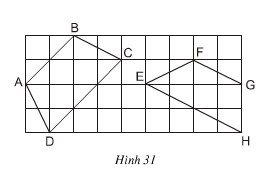
Lời giải:

Để nhận biết được tứ giác nào là hình thang cân thì phải dùng tính chất: “Hình thang cân có hai cạnh bên bằng nhau”.

• Tứ giác ABCD là hình thang cân vì AD = BC.
• Tứ giác EFGH không là hình thang cân vì EF > GH.

III. BÀI TẬP VỀ CHỨNG MINH HÌNH THANG CÂN

Bài 1. Tính độ dài các cạnh của hình thang cân ABCD trên giấy kẻ ô vuông (h.30, độ dài của cạnh ô vuông là 1cm).

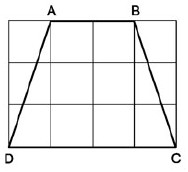
Lời giải:

Theo hình vẽ, ta có: AB = 2cm, CD = 4cm.

Áp dụng định lí Pitago trong tam giác vuông AED ta được:

AD² = AE² + ED² = 32 + 12 = 10.

Suy ra AD = √10 cm

Vậy AB = 2cm, CD = 4cm, AD = BC = √10 cm

Bài 2. Cho hình thang cân ABCD (AB // CD, AB < CD). Kẻ các đường cao AE, BF của hình thang. Chứng minh rằng DE = CF.

Lời giải:

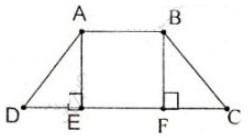
Xét hai tam giác vuông AED và BFC

Ta có: AD = BC (gt)

∠D =  ∠C (gt)

Nên  ∆AED =  ∆BFC (cạnh huyền – góc nhọn)

Suy ra: DE = CF.

Bài 3. Cho hình thang cân ABCD (AB//CD), E là giao điểm của hai đường chéo. Chứng minh rằng EA = EB, EC = ED.

Lời giải:

(*)Chứng minh ∠ACD = ∠BDC

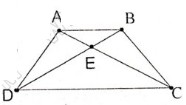
(*)Chứng minh EA = EB; EC = ED

Ta có ABCD là hình thang cân nên AB//CD ⇒ AD = BC và ∠ADC = ∠BCD

DC là cạnh chung của ΔADC và ΔBCD
⇒ ΔADC = ΔBCD (c.g.c) ⇒ ∠ACD = ∠BDC.

Ta có: ∠ACD = ∠BDC ⇒ ∠ECD = ∠EDC ⇒ΔECD cân tại E ⇒ ED = EC

Mặt khác: AC = BD (ABCD là hình thang cân)

Bài 4. Đố. Trong các tứ giác ABCD, EFGH trên giấy kẻ ô vuông (h.31), tứ giác nào là hình thang cân? Vì sao?

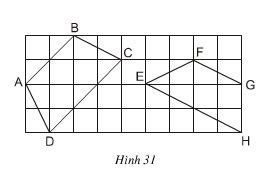
Lời giải:

Để xét xem tứ giác nào là hình thang cân ta dùng tính chất “Trong hình thang cân hai cạnh bên bằng nhau”.

Tứ giác ABCD là hình thang cân vì AD = BC.

Tứ giác EFGH không là hình thang cân vì EF > GH.

Bài 5: Cho tam giác ABC cân tại A. Trên các cạnh bên AB, AC lấy theo thứ tự các điểm D, E sao cho AD = AE

a) Chứng minh rằng BDEC là hình thang cân.

b) Tính các góc của hình thang cân đó, biết rằng góc A = 50^o.

Lời giải:

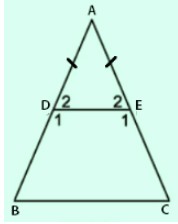
a)Ta có AD =  AE (gt) nên  ∆ADE cân

Do đó  ∠D1 = ∠E1

Trong tam giác ADE có:  ∠D1 + ∠E1+ ∠A = 1800

Hay 2∠D1= 1800 – ∠A ⇒ ∠D1= (1800 – ∠A)/2

Tương tự trong tam giác cân ABC ta có ∠B = (1800 – ∠A)/2

Nên ∠D1= ∠B mà góc  ∠D1 , ∠B là hai góc đồng vị.

Suy ra DE // BC

Do đó BDEC là hình thang.

Lại có ΔABC cân tại A ⇒ ∠B = ∠C Nên BDEC là hình thang cân.

b) Với ∠A=500 Ta được  ∠B = ∠C = (1800 – ∠A)/2 = (1800 – 500)/2
= 650

∠D2 = ∠E2= 1800  – ∠B = 1800 – 650= 1150

Bài 6: Cho tam giác ABC cân tại A, các đường phân giác BD, CE (D ∈ AC, E ∈ AB). Chứng minh rằng BEDC là hình thang cân có đáy nhỏ bằng cạnh bên.

Lời giải:

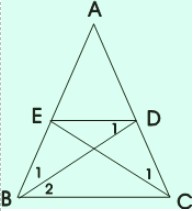
a) ΔABD và ΔACE có:

AB = AC (gt)

∠A chung; ∠B1 = ∠C1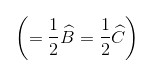

Nên ΔABD = ΔACE (g.c.g)

Suy ra AD = AE.

Chứng minh BEDC là hình thang cân như câu a của bài 15.

b) Vì BEDC là hìnhthang cân nên DE // BC.

Suy ra ∠D1 = ∠B2 (so le trong)

Lại có  ∠B2 = ∠B1  nên ∠B1= ∠A1

Do đó tam giác EBD cân. Suy ra EB = ED.

Vậy BEDC là hình-thang-cân có đáy nhỏ bằng cạnh bên.

Bài 7: Hình thang ABCD (AB // CD) có ∠ACD = ∠BDC. Chứng minh rằng ABCD là hình thang cân.

Lời giải:

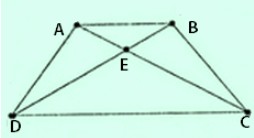
Gọi E là giao điểm của AC và BD.

∆ECD có ∠C1 = ∠D1 (do ∠ACD = ∠BDC) nên là tam giác cân.

Suy ra EC = ED        (1)

Tương tự ∆EAB cân tại A  suy ra: EA = EB      (2)

Từ (1) và (2) ta có: EA + EC = EB + ED ⇒ AC = BD

Hình thang ABCD có hai đường chéo bằng nhau nên là hình thang cân.

Bài 8: Chứng minh định lý: “Hình thang có hai đường chéo bằng nhau là hình thang cân” qua bài toán sau: Cho hình thang ABCD (AB // CD) có AC = BD. Qua B kẻ đường thẳng song song với AC, cắt đường thẳng DC tại tại E. Chứng minh rằng:

a) ΔBDE là tam giác cân.

b) ΔACD = ΔBDC

c) Hình thang ABCD là hình thang cân.

Lời giải:

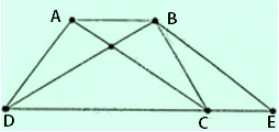
a) Ta có AB//CD suy ra AB // CE  và AC//BE

Xét Hình thang ABEC (AB // CE) có hai cạnh bên AC, BE song song nên chúng bằng nhau:  AC = BE   (1)

Theo giả thiết AC = BD    (2)

Từ (1) và (2) suy ra BE = BD do đó tam giác BDE cân.

b) Ta có AC // BE suy ra ∠C1 = ∠E      (3)

∆BDE cân tại B (câu a) nên  ∠D1 = ∠E    (4)

Từ (3) và (4) suy ra ∠C1 =  ∠D1

Xét  ∆ACD và  ∆BCD có AC = BD (gt)

∠C1 =  ∠D1     (cmt)

CD cạnh chung

Nên ∆ACD = ∆BDC (c.g.c)

c) ∆ACD = ∆BDC (câu b)

Suy ra ∠ADC = ∠BD

Hình thang ABCD có hai góc kề một đáy bằng nhau nên là hình thang-cân.

Bài 9 : Hình thang ABCD (AB//CD) có A – D = 20^o, B = 2C . Tính các góc của hình thang.

Giải.

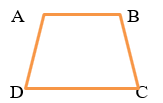
Vì ABCD là hình thang (AB//CD), nên ta có :

B + C = 180^o (hai góc trong cùng phía bù nhau)

2C + C = 180^o ( vì B = 2C)

3C = 180^o → C = 60^o → B = 2.60^o = 120^o

A – D = 20^o → A = 20 + D

A + D = 180^o (hai góc trong cùng phía bù nhau)

20 + D + D = 180

2D = 160 → D = 80 →à A = 20 + 80 = 100

Vậy A = 100 ; B = 120 ; C = 60 ; D = 80.

Bài 10 Tứ giác ABCD có AB = BC và AC là tia phân giác của góc A. Chứng minh rằng từ giác ABCD là hình thang.

Gợi ý :

AB = BC để làm gì?

AC là tia phân giác để làm gì?

Bài 11: Tứ giác ABCD có BC = CD và BD là tia phân giác của góc D. Chứng minh rằng ABCD là hình thang.

Gợi ý : vẽ hình và làm tương tự bài toán 3.

Cách chứng minh một tứ giác là hình thang à chứng minh 2 cạnh song song à 2 góc đồng vị bằng nhau, so le trong bằng nhau hoặc trong cùng phía bù nhau.

Bà 12: Hình thang vuông ABCD có A = D = 90^o, C = 45^o . Biết đường cao bằng 4cm. AB + CD = 10cm, Tính hai đáy.

Gợi ý :

• Vẽ hình
• Đường cao AD = 4cm.
• Dựng đường cao BH à BH = AB = 4cm.
• Tam giác BHC vuông tại H và C = 45^o à tam giác BHC là tam giác vuông cân à BH = CH = 4cm.
• AB + CD = 10

AB + DH + CH = 10

AB + AB + 4 = 10 (vì AB = DH)

2AB = 6 → AB = 3 →  DH = 3 →  DC = DH + CH = 3 + 4 = 7cm

Bài 13 : Cho tam giác ABC cân tại A, các đường phân giác BD, CE (D

AC, E  AB). Chứng minh rằng BEDC là hình thang cân có đáy nhỏ bằng cạnh bên.

Gợi ý :

Bước 1 : Chứng minh tứ giác BEDC là hình thang (hai góc đồng vị AED = ABC tính thông qua góc chung A của 2 tam giác cân ABC và tam giác cân AED à chứng minh tam giác AED là tam giác cân à chứng minh AE = AD)

Bước 2 : BEDC là hình thang dễ dàng thấy B = C (vì tam giác ABC cân tại A) à là hình thang cân.

Bài 14 : Cho hình thang cân ABCD, có đáy nhỏ AB bằng cạnh bên AD. Chứng minh rằng AC là tia phân giác của góc C.

Gợi ý :

ABCD là hình thang cân, đáy nhỏ AB

AB = AD (gt)

BC = AD (vì ABCD là hình thang cân)

Nên tam giác ABC cân tại B à học sinh tự tư duy tiếp.

Bài 15 : Cho tam giác ABC cân tại A. Trên cạnh bên AB, AC lấy các điểm M, N sao cho BM = CN.

a) Chứng minh tứ giác BMNC là hình thang cân.

b)Tính các góc của tứ giác BMNC biết rằng A = 40^o.

Gợi ý : tứ giác BMNC là hình thang cân  BMNC là hình thang (đồng vị, so le trong, trong cùng phía bù nhau)  hình thang cân (2 cách chứng minh hình thang cân).

Vậy là các bạn vừa được chia sẻ cách chứng minh hình thang cân nhanh nhất và nhiều bài tập vận dụng. Hi vọng, chia sẻ cùng bài viết, bạn đã có thêm nhiều bí kíp hay trong việc chứng minh hình thang nói chung, hình thang cân nói riêng. Cảm ơn các bạn đã đồng hành cùng bài viết ! Hẹn gặp lại các bạn trong những bài viết sau !

Bản quyền bài viết thuộc Trường Trung Cấp Nghề Thương Mại Du Lịch Thanh Hoá. Mọi hành vi sao chép đều là gian lận!
Nguồn chia sẻ: https://tmdl.edu.vn https://tmdl.edu.vn/cach-chung-minh-hinh-thang-can-nhanh-nhat-va-bai-tap-van-dung/

Trang chủ: tmdl.edu.vn
Danh mục bài: Giáo dục