Căn thức (căn bậc 2, căn bậc 3) là nội dung kiến thức mà các em học ở ngay chương 1 đại số lớp 9, phần bài tập về căn thức cũng thường xuyên xuất hiện trong đề thi tuyển sinh vào lớp 10 THPT.
Có nhiều dạng bài tập về căn thức như: rút gọn biểu thức, tính giá trị của biểu thức, giải phương trình, hệ phương trình,… Tuy nhiên, trong bài viết này chúng ta tập trung tìm hiểu cách giải phương trình chứa dấu căn, qua đó vận dụng giải một số bài tập về phương trình chứa căn thức để rèn luyện kỹ năng giải toán.
Bạn đang xem bài: Cách giải phương trình chứa dấu căn và Bài tập vận dụng – Toán lớp 9
I. Kiến thức cần nhớ khi giải phương trình chứa dấu căn
• 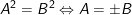
• 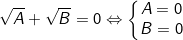
• 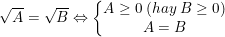
• 
• 
• 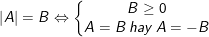
• 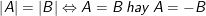
• 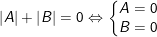
• 
• 
• 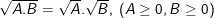
• 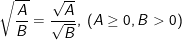
II. Cách giải Phương trình có chứa dấu căn
1. Giải phương trình chứa căn thức dạng:  với e ≥ 0 là hằng số
với e ≥ 0 là hằng số
i) Trường hợp: 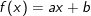 hoặc
hoặc 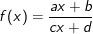 thì:
thì:
+ Bước 1: Tìm điều kiện của x để f(x) ≥ 0
+ Bước 2: Bình phương 2 vế phương trình để khử căn.
+ Bước 3: Giải phương trình để tìm nghiệm x thỏa mãn điều kiện
* Ví dụ 1 (Bài 25 trang 16 SGK Toán 9 Tập 1): Tìm x?
a)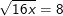 b)
b) 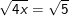
c)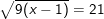 d)
d)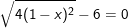
° Lời giải:
a)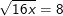 (*)
(*)
– Điều kiện: x ≥ 0, khi đó bình phương 2 vế ta có:
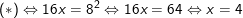
– Ta thấy x = 4 thỏa điều kiện nên pt có nghiệm x = 4.
b) 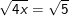 (*)
(*)
– Điều kiện: x ≥ 0, khi đó bình phương 2 vế ta có:
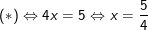
– Ta thấy x = 5/4 thỏa điều kiện nên pt có nghiệm x = 5/4.
c)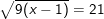 (*)
(*)
– Điều kiện: x – 1 ≥ 0 ⇔ x ≥ 1; khi đó ta có (ở bày này ta có thể rút gọn hệ số trước khi bình phương 2 vế):
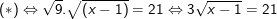
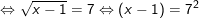
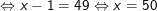
– Ta thấy x = 50 thỏa điều kiện nên pt có nghiệm x = 50.
d)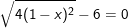 (*)
(*)
– Vì (1 – x)2 ≥ 0 ∀x nên pt xác định với mọi giá trị của x.
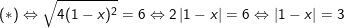
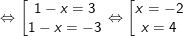
→ Vậy phương trình có 2 nghiệm x = -2 hoặc x = 4
* Ví dụ 2: Giải các phương trình sau:
a)  b)
b) 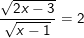
° Lời giải:
a)  (*)
(*)
– Điều kiện: 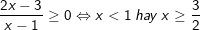
– Khi đó bình phương 2 vế ta được:
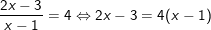
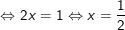
– Đối chiếu điều kiện (x < 1 hoặc x ≥ 3/2) ta thấy x = 1/2 thỏa điều kiện, nên ta nhận nghiệm này. Kết luận pt có nghiệm x = 1/2.
b) 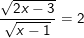 (*)
(*)
– Điều kiện: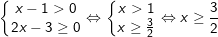
– Khi đó bình phương 2 vế ta được:

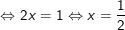
– Đối chiếu điều kiện (x ≥ 3/2) ta thấy x = 1/2 không thỏa điều kiện này, nên ta KHÔNG nhận nghiệm này. Kết luận pt vô nghiệm.
ii) Trường hợp:  (*) thì ta cần kiểm tra biểu thức f(x).
(*) thì ta cần kiểm tra biểu thức f(x).
+) Nếu f(x) = ax2 + bx + c = (Ax ± B)2 tức là có dạng hằng đẳng thức thì KHAI CĂN, tức là:
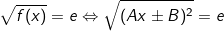
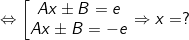
+) Nếu  không có dạng hằng đẳng thức thì ta thực hiện các bước sau:
không có dạng hằng đẳng thức thì ta thực hiện các bước sau:
– Bước 1: Điều kiện f(x) ≥ 0
– Bước 2: Bình phương 2 vế phương trình để khử căn thức
– Bước 3: Giải phương trình bậc 2 (bằng cách phân tích thành nhân tử đưa về pt tích).
* Ví dụ 1: Giải phương trình sau: 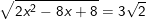 (*)
(*)
° Lời giải:
– Vì: 2x2 – 8x + 8 = 2(x2 – 4x + 4) = 2(x – 2)2 nên ta có:

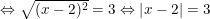
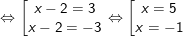
* Ví dụ 2: Giải phương trình sau: 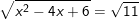 (*)
(*)
° Lời giải:
– Ta thấy: x2 – 4x + 6 = x2 – 4x + 4 + 2 = (x – 2)2 + 2 không có dạng (Ax ± B)2nên ta thực hiện như sau:
– Điều kiện: x2 – 4x + 6 ≥ 0 ⇔ (x – 2)2 + 2 ≥ 0 ∀x nên biểu thức xác định với mọi giá trị của x.
– Bình phương 2 vế phương trình ta được:
(x – 2)2 + 2 = 11 ⇔ (x – 2)2 = 9 
– Kết luận: Phương trình có 2 nghiệm x = -1 và x = 5.
2. Giải phương trình chứa dấu căn dạng: 
* Phương pháp giải:
– Bước 1: Viết điều kiện của phương trình: 
– Bước 2: Nhận dạng từng loại tương ứng với các cách giải sau:
¤ Loại 1: Nếu f(x) có dạng hằng đẳng thức (Ax ± B)2 thì khai căn đưa về phương trình trị tuyệt đối để giải.
¤ Loại 2: Nếu f(x) = Ax ± B và g(x) = Ex ± D thì dùng phương pháp bình phương 2 vế.
¤ Loại 3: Nếu f(x) = Ax2 + Bx + C [không có dạng hằng đẳng thức (Ax ± B)2] và g(x) = Ex ± D thì dùng phương pháp bình phương 2 vế.
¤ Loại 4: Nếu f(x) = Ax2 + Bx + C và g(x) = Ex2 + Dx + F thì thử phân tích f(x) và g(x) thành nhân tử, nếu chúng có nhân tử chung thì đặt nhân tử chung đưa về phương trình tích.
– Bước 3: Kiểm tra nghiệm tìm được có thỏa mãn điều kiện không sau đó kết luận nghiệm của phương trình.
* Ví dụ 1: Giải phương trình sau: 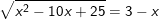
° Lời giải:
– Ta có: 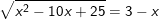
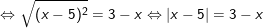
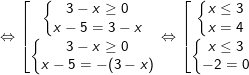
– Vậy phương trình vô nghiệm
* Ví dụ 2: Giải phương trình sau: 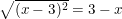 (*)
(*)
° Lời giải:
– Ta có: 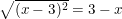

– Vậy phương trình có vô số nghiệm x ≤ 3.
* Ví dụ 3: Giải phương trình sau:
° Lời giải:
– Điều kiện: 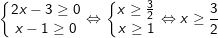
– Bình phương 2 vế ta được:
2x – 3 = (x – 1)2 ⇔ 2x – 3 = x2 – 2x + 1
⇔ x2 – 4x + 4 = 0 ⇔ (x – 2)2 = 0 ⇔ x = 2.
– Đối chiếu với điều kiện ta thấy x = 2 thỏa điều kiện nên phương trình nhận nghiệm này.
– Phương trình có nghiệm x = 2.
* Ví dụ 4: Giải phương trình sau: (*)
(*)
° Lời giải:
– Ta thấy: f(x) = x2 – 5x – 6 không có dạng hằng đẳng thức (Ax ± B)2 (và vế phải là dạng hàm bậc 1) nên để khử căn ta dùng phương pháp bình phương 2 vế.
– Điều kiện: 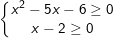 khi đó ta bình phương 2 vế được:
khi đó ta bình phương 2 vế được:
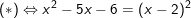

– Kiểm tra x = -10 có thỏa mãn điều kiện không bằng cách thay giá trị này vào các biểu thức điều kiện thấy không thỏa
→ Vậy phương trình vô nghiệm.
3. Giải phương trình chứa dấu căn dạng: ![small sqrt{[f(x)]^2}pm sqrt{[h(x)]^2}=g(x) 1596080259w0j8iuwr7k 1607563722 1628739188](https://tmdl.edu.vn/wp-content/uploads/2022/12/1596080259w0j8iuwr7k_1607563722_1628739188.gif)
* Để giải phương trình dạng này ta thực hiện các bước sau:
– Bước 1: Nếu f(x) và h(x) có chứa căn thì phải có điều kiện biểu thức trong căn ≥ 0.
– Bước 2: Khử căn thức đưa phương trình về dạng pt trị tuyệt đối: |f(x)| ± |h(x)| = g(x).
– Bước 3: Xét dấu trị tuyệt đối (khử trị tuyệt đối) để giải phương trình.
* Ví dụ 1: Giải phương trình:  (*)
(*)
° Lời giải:
– Điều kiện: x ≥ 0.
– Mặt khác, ta thấy:  và
và  nên ta có:
nên ta có:
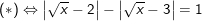 (**)
(**)
– Ta xét các trường hợp để phá dấu trị tuyệt đối:
+) TH1: Nếu 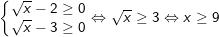 , ta có:
, ta có:
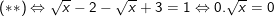
⇒ Phương trình có vô số nghiệm x ≥ 9.
+) TH2: Nếu 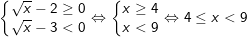 , ta có:
, ta có:
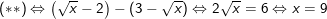
– Đối chiếu điều kiện ta thấy x = 9 không thỏa đk nên loại.
+) TH3: Nếu 
+) TH4: Nếu 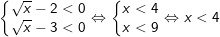 , ta có:
, ta có:
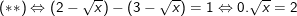
→ Phương trình vô nghiệm.
⇒ Kết luận: Vậy phương trình có vô số nghiệm x ≥ 9.
* Ví dụ 2: Giải phương trình: 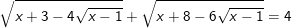
° Lời giải:
– Điều kiện: x ≥ 1
– Nhận thấy: 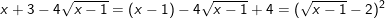

– Đến đây xét các trường hợp giải tương tự ví dụ 1 ở trên.
4. Cách giải một số phương trình chứa căn khác.
i) Phương pháp đặt ẩn phụ để giải phương trình chứa dấu căn.
* Ví dụ 1: Giải phương trình sau:  (*)
(*)
° Lời giải:
– Điều kiện: x ≥ 0
Đặt  khi đó ta có pt (*) trở thành:
khi đó ta có pt (*) trở thành:
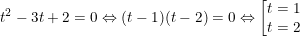
– Cả 2 nghiệm t đều thỏa điều kiện nên ta có:
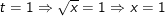
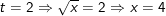
(Cách giải pt bậc 2 một ẩn các em sẽ học ở nội dung bài chương sau).
* Ví dụ 2: Giải phương trình sau: 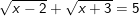 (*)
(*)
° Lời giải:
– Điều kiện: 
Đặt 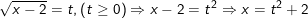 , khi đó pt(*) trở thành:
, khi đó pt(*) trở thành:

– Ta thấy pt(**) có dạng ở mục 2) loại 3; với điều kiện 5 – t ≥ 0 ⇔ t ≤ 5; ta bình phương 2 vế (**) được:
t2 + 5 = (5 – t)2 ⇔ t2 + 5 = t2 – 10t + 25 ⇔ 10t = 20 ⇔ t= 2
– Với t = 2 thỏa điều kiện 0≤ t ≤ 5 nên ta có:
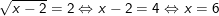
→ Phương trình có nghiệm x = 6.
* Ví dụ 3: Giải phương trình sau: 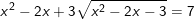 (*)
(*)
° Lời giải:
– Điều kiện: x2 – 2x – 3 ≥ 0. Khi đó ta có:

Đặt  khi đó pt(**) trở thành:
khi đó pt(**) trở thành:
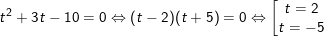
– Đối chiếu điều kiện thì t = -5 loại và t = 2 nhận.
Với t = 2 ⇒ x2 – 2x – 3 = 4 ⇔ x2 – 2x – 7 = 0 ⇔ (x2 – 2x + 1) – 8 = 0.

– Kiểm tra thấy 2 nghiệm x trên thỏa điều kiện nên pt có 2 nghiệm. x = 1 ± 2√2.
ii) phương pháp đánh giá biểu thức dưới dấu căn (lớn hơn hoặc nhỏ hơn 1 hằng số) để giải phương trình chứa căn thức.
– Áp dụng với phương trình chứa căn thức dạng: ![small sqrt{[f(x)]^2+c}+sqrt{[h(x)]^2+d}=pm [g(x)]^2+e 1596080313bglsi08wkw 1607563729 1628739215](https://tmdl.edu.vn/wp-content/uploads/2022/12/1596080313bglsi08wkw_1607563729_1628739215.gif) (với c,d>0 và c+d=e)
(với c,d>0 và c+d=e)
– PT có thể cho ngay dạng này hoặc có thể tách một hệ số nào đó để có [f(x)]2; [h(x)]2 hay [g(x)]2;
* Ví dụ: Giải phương trình sau:  (*)
(*)
° Lời giải:
– Ta nhận thấy:


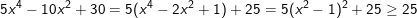
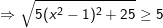
– Do đó:  dấu “=” xảy ra khi và chỉ khi:
dấu “=” xảy ra khi và chỉ khi:

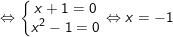
→ Vậy phương trình có nghiệm x = -1.
III. Một số bài tập về phương trình có chứa dấu căn
* Bài 1: Giải các phương trình sau:
a)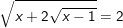
b)
* Bài 2: Giải các phương trình sau:
a)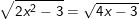
b)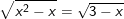
c)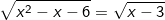
* Bài 3: Giải các phương trình sau
a)
b)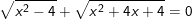
c)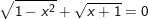
d)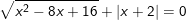
Hy vọng với bài viết về cách giải phương trình chứa dấu căn ở trên giúp các em hiểu rõ hơn phương pháp giải các dạng toán căn thức này. Qua đó dễ dàng giải các bài toán tương tự khi gặp. Chúc các em học tập tốt.
Bản quyền bài viết thuộc trường Trường Trung Cấp Nghề Thương Mại Du Lịch Thanh Hoá. Mọi hành vi sao chép đều là gian lận!
Nguồn chia sẻ: Trường Tmdl.edu.vn (tmdl.edu.vn)
Trang chủ: tmdl.edu.vn
Danh mục bài: Giáo dục




