Cùng Tmdl.edu.vn tìm hiểu Cách tìm điểm đối xứng của một điểm qua đường thẳng – Toán 10 chuyên đề
Vậy cách tìm điểm đối xứng của một điểm qua đường thẳng như thế nào? chúng ta sẽ cùng tìm hiểu qua bài viết dưới đây và cùng xem các bài tập và ví dụ minh họa để hiểu rõ nhé.
Bạn đang xem bài: Cách tìm điểm đối xứng của một điểm qua đường thẳng – Toán 10 chuyên đề
Các em có thể xem lại nội dung phương trình tổng quát, phương trình tham số, phương trình chính tắc của đường thẳng nếu các em chưa nhớ rõ phần kiến thức này.
° Cách tìm điểm đối xứng của một điểm qua đường thẳng
• Cách giải 1:
* Giải sử cần tìm điểm M’ đối xứng với M qua (d), ta làm như sau:
– Tìm hình chiếu H của M lên (d). (xem ngay cách tìm hình chiếu của một điểm lên đường thẳng).
– M’ đối xứng với M qua (d) nên M’ đối xứng với M qua H (khi đó H là trung điểm của M và M’).
• Cách giải 2:
– Gọi M’ là điểm đối xứng của M(x;y) qua d: ax + by + c = 0 và H là trung điểm của MM’ thì điều kiện:
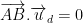(1)
Và 
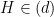(2)
– Giải hệ từ (1) và (2) ta suy ra tọa độ điểm M’
* Ví dụ 1: Tìm điểm của điểm M’ đối xứng với M(3;-1) qua đường thẳng (d) có phương trình: x + 2y – 6 = 0
* Lời giải:
¤ Đầu tiên ta tìm hình chiếu H của M(3;-1) lên (d).
– Gọi (d’) là đường thẳng đi qua M và vuông góc với (d)
– Vì (d) có phương trình: x + 2y – 6 = 0 nên VTPT của (d) là: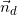 
= (1;2)
– Lại có (d’) ⊥ (d) nên (d’) nhận VTPT của (d) là VTCP ⇒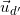 
=(1;2)
– Phương trình đường thẳng (d’) qua M(3;-1) có VTCP 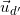(1;2) là:
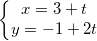
– Vì H là hình chiếu của M thì H là giao điểm của (d) và (d’) nên có:
Thay x,y từ (d’) và phương trình (d), ta có:
(3+t) + 2(-1+2t) – 6 = 0
⇔ 5t – 5 = 0 ⇔ t =1
⇒ x = 4, y = 1 là toạ độ điểm H.
Vậy tọa độ H(4;1)
¤ Khi đó H là trung điểm của M(3;-1) và M'(xM’;yM‘), ta có:
; 
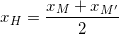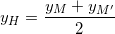
⇒ xM’ = 2xH – xM = 2.4 – 3 = 5
⇒ yM’ = 2yH – yM = 2.1 – (-1) = 3
⇒ Điểm M'(5;3) là điểm đối xứng của M(3;-1) lên (d): x + 2y – 6 = 0
* Ví dụ 2: Tìm tọa độ điểm M’ đối xứng với M(2;3) qua đường thẳng d: y = x.
* Lời giải:
– Gọi M'(x;y) là điểm đối xứng với M qua d và H là trung điểm của MM’
Khi đó M, M’ đối xứng nhau qua d: x – y = 0 thì điều kiện là: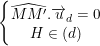 
– Ta có: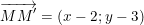 
;
; 
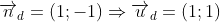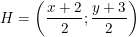
Từ điều kiện trên ta có:
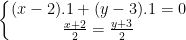
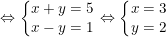
Vậy suy ra: M'(3;2)
Như vậy, tùy vào bài toán và cách nào các em cảm thấy mình vận dụng nhuần nhuyễn hơn, cách nào giúp em thấy dễ nhớ hơn thì các em có thể chọn làm theo để ghi nhớ thật kỹ nhé.
Theo Tmdl.edu.vn đánh giá, thì cách 2 vận dụng sẽ tốt hơn cách 1 và giúp bài giải của chúng ta ngắn gọn hơn.
Hy vọng với bài viết Cách tìm điểm đối xứng của một điểm qua đường thẳng ở trên hữu ích cho các em. Mọi thắc mắc các em vui lòng để lại bình luận dưới bài viết để Tmdl.edu.vn ghi nhận và hỗ trợ. Chúc các em học tập tốt!
Bản quyền bài viết thuộc trường Trường Trung Cấp Nghề Thương Mại Du Lịch Thanh Hoá. Mọi hành vi sao chép đều là gian lận!
Nguồn chia sẻ: Trường Tmdl.edu.vn (tmdl.edu.vn)
Trang chủ: tmdl.edu.vn
Danh mục bài: Giáo dục
