Cách tìm X lớp 6 lũy thừa nâng cao sẽ là nội dung chính mà các Trường Trung Cấp Nghề Thương Mại Du Lịch Thanh Hoá sẽ hướng dẫn các em trong bài học hôm nay. Trước khi đi tìm x lớp 6 lũy thừa nâng cao. Các em cùng ôn lại kiến thức về lũy thừa nhé.

Lý thuyết Lũy thừa với số mũ tự nhiên
Lũy thừa là gì?
Phép tính a lũy thừa b ký hiệu là ab, a là cơ số, b là số mũ.
Bạn đang xem bài: Cách tìm X lớp 6 lũy thừa nâng cao (bài tập chi tiết dễ hiểu)
Phép lũy thừa đặc biệt:
- a² còn gọi là “a bình phương”.
- a³ còn gọi là “a lập phương”.
Lũy thừa với số mũ tự nhiên
Lũy thừa bậc n của a là tích của n thừa số bằng nhau, mỗi thừa số bằng a:
(n thừa số a) (a khác 0)
a được gọi là cơ số; n được gọi là số mũ.
Nhân hai lũy thừa cùng cơ số
Khi nhân hai lũy thừa cùng cơ số, ta giữa nguyên cơ số và cộng các số mũ.
Chia hai lũy thừa cùng cơ số
Khi chia hai lũy thừa cùng cơ số (khác 0), ta giữ nguyên cơ số và trừ các số mũ cho nhau.
Lũy thừa của lũy thừa
Ví dụ:
Nhân hai lũy thừa cùng số mũ, khác cơ số
Ví dụ :
Chia hai lũy thừa cùng số mũ, khác cơ số
Ví dụ :
Một vài quy ước
1n = 1 ví dụ : 12017 = 1
a0 = 1 ví dụ : 20170 = 1
Một số tính chất lũy thừa
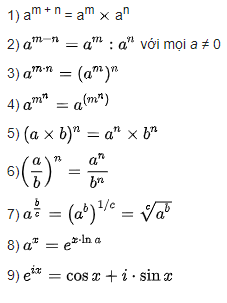

Lũy thừa với số mũ nguyên âm

Cách tìm X lớp 6 lũy thừa nâng cao
Bài tập 1: Cách tìm x lớp 6 dạng lũy thừa biết ( 2x + 1)³ = 125. Các em xem video hướng dẫn giải bên dưới nhé:
Bài tập 2: Cách tìm x lớp 6 dạng lũy nâng cao
Bài tập 3: Cách tìm x lớp 6 dạng lũy nâng cao
Bài tập 4: Tìm số tự nhiên x, biết rằng:
2x + 2x + 3 = 144
Lời giải:
Ta có: 2x + 2x + 3 = 144
=> 2x + 2x.23 = 144
=> 2x.(1 + 8) = 144
=> 2x.9 = 144
=> 2x = 144 : 9 = 16 = 24
=> x = 4.
Bài tập 5 Tìm tập hợp các số tự nhiên x, biết rằng lũy thừa 52x – 1 thỏa mãn điều kiện:
100 < 52x – 1 < 56.
Lời giải:
Ta có: 100 < 52x – 1 < 56
=> 52 < 100 < 52x-1 < 56
=> 2 < 2x – 1 < 6
=> 2 + 1 < 2x < 6 + 1
=> 3 < 2x < 7
Vì x ∈ N nên suy ra: x ∈ {2; 3} là thỏa mãn.
Hy vọng với bài học về tìm X lớp 6 lũy thừa nâng cao sẽ giúp cho các em ôn tập và củng cố các dạng bài tập, rèn luyện kỹ năng giải toán lũy thừa lớp 6. Thầy cô chúc các em học thật tốt nhé.
Bản quyền bài viết thuộc Trường Trung Cấp Nghề Thương Mại Du Lịch Thanh Hoá. Mọi hành vi sao chép đều là gian lận!
Nguồn chia sẻ: https://tmdl.edu.vn https://tmdl.edu.vn/cach-tim-x-lop-6-luy-thua-nang-cao/
Trang chủ: tmdl.edu.vn
Danh mục bài: Giáo dục