Chuyên đề về hàm số – toán 7: định nghĩa, tính chất và các dạng bài tập
Chuyên đề về hàm số từ định nghĩa đến tính chất và các dạng toán thường gặp là những nội dung quan trọng Zixabooks.com sẽ chia sẻ qua bài viết này. Đậy là phần kiến thức Toán, phân môn Đại số trọng tâm của chương trình. Hãy chia sẻ bài viết sau đây để nắm vững hơn các kiến thức cần ghi nhớ bạn nhé !
I. LÝ THUYẾT CHUNG VỀ HÀM SỐ
Bạn đang xem bài: Chuyên đề về hàm số – toán 7: định nghĩa, tính chất và các dạng bài tập
1. Định nghĩa
Nếu đại lượng y phụ thuộc vào đại lượng thay đổi x sao cho với mỗi giá trị của x ta luôn xác định được chỉ một giá trị tương ứng của y thì y được gọi là hàm số của x và x gọi là biến số
Nhận xét: Nếu đại lượng y là hàm số của đại lượng x thì mỗi giá trị của đại lượng x đều có một giá trị tương ứng duy nhất của đại lượng y( hay mỗi giá trị của x không thể có hơn một giá trị tương ứng của đại lượng y)
Chú ý:
+ Khi x thay đổi mà y luôn nhận một giá trị thì y được gọi là hàm hằng
+ Hàm số có thể được cho bằng bảng, bằng công thức,…
+ Khi y là hàm số của x ta có thể viết: y = f(x); y = g(x);…
Ví dụ:
Có các hàm số như sau: y = 2x; y = -x; y = -x/2;…
2. Các dạng hàm số
- Đơn ảnh, song ảnh, toàn ảnh
- Hàm hợp và hàm ngược
3. Các tính chất của hàm số
- Tính đơn điệu
- Tính chẵn lẻ

II. CÁC DẠNG TOÁN VỀ HÀM SỐ LỚP 7
1. Dạng 1: Xác định đại lượng y có phải là hàm số của đại lượng x hay không
Phương pháp giải:
- Kiểm tra điều kiện: mỗi giá trị của x được tương ứng với 1 giá trị của y.
- Đại lượng y có phải là hàm số của đại lượng x hay không.
- Vì mỗi giá trị của x luôn luôn xác định được chỉ một giá trị tương ứng của y nên đại lượng y là hàm số của đại lượng x.
Ví dụ 1: Đại lượng x lấy các giá trị là các số tự nhiên, đại lượng y lấy giá trị là số dư của phép chia x cho 3. Đại lượng y có phải là hàm số cảu đại lượng x không?
Gợi ý: Đại lượng y là hàm số của đại lượng x vì ứng với mỗi giá trị tương ứng của x ta luôn xác định được chỉ một giá trị của y
Ví dụ 2: Bảng sau đây có cho ta một hàm số không? Nếu không thì thay đổi như thế nào để được một hàm số:

Hướng dẫn:
Bảng này không xác định hàm số vì giá trị x = 6 không có giá trị tương ứng của y.
Có thể thay đổi bằng một trong hai cách
– Với x = 6 cho thêm một giá trị tương ứng của y.
– Bỏ giá trị 6 của x.
2. Dạng 2: Tính giá trị của hàm số khi biết giá trị của biến
Phương pháp giải:
- Nếu hàm số cho bằng bảng thì cặp giá trị tương ứng của x và y nằm cùng một cột.
- Nếu hàm số cho bằng công thức ta thay giá trị của biến đã cho vào công thức để tính giá trị tương ứng của hàm số.
Ví dụ 1:
Bảng sau đây có xác định một hàm số không? Tìm giá trị của y tại x = – 2,3 ; x = – 4,5 ; x = 0.

Hướng dẫn:
Bảng này có xác định đại lượng y là hàm số của đại lượng x.
Khi x = -2,3 thì y = 5, khi x = – 4,5 thì y = 7, khi x = 0 thì y = 2.
Ví dụ 2:
Một hàm số được cho bằng công thức: y = f(x) = – x² + 2.
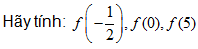
Hướng dẫn:
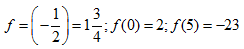
Dạng 3: Viết công thức xác định hàm số
Ví dụ: Một hàm số được cho bằng bảng sau:
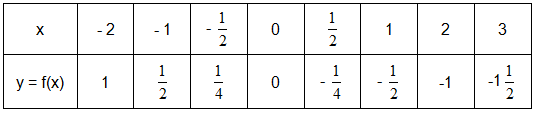
a) Tìm f(-1), f(0), f(2).
b) Hàm số này có thể được cho bằng công thức nào?
Giải:
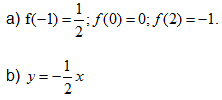
III. BÀI TẬP CHUYÊN ĐỀ HÀM SỐ LỚP 7
1. Các công thức sau đây có chứng tỏ rằng đại lượng y là hàm số cảu đại lượng x hay không?
a) y – 3 = x ;
b) – 2y = x ;
c) y² = x.
Gợi ý:
a) y = x + c3 : Đại lượng y là hàm số của đại lượng x
b) y = – 0.5x : Đại lượng y là hàm số của đại lượng x.
c) y² = x : Đại lượng y không phải là hàm số của đại lượng x. Chẳng hạn, ứng với x = 1 có hia giá trị của y là ± 1.
2. Đại lượng y có phải là hàm số của đại lượng x không, nếu bảng các giá trị tương ứng của chúng là:
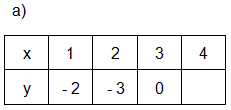
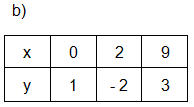
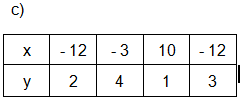


Gợi ý:
a) Không phải hàm số vì giá trị x = 4 không có giá trọ tương ứng của y.
b) Là hàm số.
c) Không phải hàm số vì giá trị x = -12 có hai giá trị tương ứng khác nhau của y (2 và 3).
d) Là hàm số.
e) Không phải hàm số vì các giá trị của x không phải là các số.
3. Đại lượng x lấy các giá trị là các số tự nhiên, đại lượng y lấy giá trị là ước của x. Đại lượng y có phải là hàm số của đại lượng x không?
Gợi ý: Đại lượng y không phải làm hàm số của đại lượng x vì ứng với giá trị x = 5 chẳng hạn ta có hai giá trị của y (ước tự nhiên của 5 là 1 và 5)
4. Bảng sau đây có xác định một hàm số không? Nếu không thì thay đổi như thế nào để được một hàm số:

Gợi ý:
Bảng này không xác địng hàm số vì giá trị x = 4 có giá trị tương ứng của y (-2 và – 4).
Có thể thay đổi bằng cách bỏ một trong hai cặp (x= 4, y = -3) hoặc (x = 4, y = -4).
5.
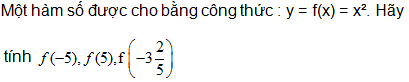
Gợi ý:
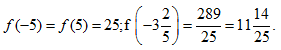
6. Cho hình vuông có cạnh x. Viết công thức của hàm số cho tương ứng cạnh x của hình vuông với:
a) Chu vi y của nó.
b) Diện tích y của nó.
Gợi ý:
a) y = 4x
b) y = x²
7. Đại lượng y = f(x) là hàm số của đại lượng x, biết rằng:
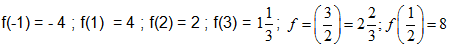
a) Lập bảng các giá trị tương ứng của x và y.
b) Viết công thức xác định hàm số này.
Gợi ý:
a)
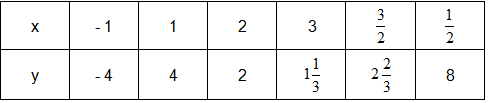
b)
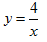
8. Đại lượng x lấy giá trị là các số thực, đại lượng y lấy giá trị bằng x nếu x ≥ 0, bằng – x nếu x < 0
a) Đại lượng y có phải là hàm số của đại lượng x không?
b) Nếu có, hãy viết công thức xác định hàm số này.
Gợi ý:
a) y là hàm số của x;
b) y = |x|
9.

Gợi ý:

10.
Một hàm số được xác định như sau:
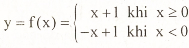
a) Tính f(3) , f(-3).
b) Có cách nào viết gọn công thức trên không?
Gợi ý:
a) f(3) = 4 ; f(-3) = 4
b) y = f(x) = |x| + 1.
Trên đây, chúng tối đã giới thiệu trọn vẹn các kiến thức cần ghi nhớ về chuyên đề hàm số và các dạng bài tập thường gặp. Hi vọng, bạn nắm vững hơn mảng kiến thức Đại số 7 quan trọng này. Hãy lưu lại để xem khi cần bạn nhé ! Đại lượng tỉ lệ thuận, đại lượng lệ nghịch cũng đã được Trường Trung Cấp Nghề Thương Mại Du Lịch Thanh Hoá giới thiệu rất chi tiết. Bạn tham khảo thêm nhé !
tmdl.edu.vn. Mọi hành vi sao chép đều là gian lận!
Nguồn chia sẻ: https://tmdl.edu.vn/chuyen-de-ve-ham-so-toan-7-dinh-nghia-tinh-chat-va-cac-dang-bai-tap/
Trang chủ: tmdl.edu.vn
Danh mục bài: Giáo dục



