Trong tam giác vuông, ngoài định lý Pitago các em đã được giới thiệu còn nhiều hệ thức lượng thể hiện mối quan hệ giữa góc và cạnh, cạnh và đường cao, cạnh và góc, góc và góc,… trong tam giác vuông
Vậy các hệ thức lượng thể hiện mối quan hệ giữa đường cao cạnh, góc của tam giác vuông có công thức được viết như thế nào? chúng ta hãy hệ thống lại qua bài viết này.
Bạn đang xem bài: Công thức hệ thức lượng trong tam giác vuông, tỉ số lượng giác của góc nhọn – Toán lớp 9
I. Các hệ thức về cạnh và đường cao trong tam giác vuông
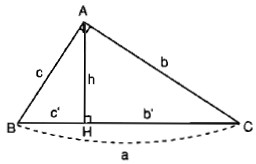
– Cho tam giác vuông như hình, ta có:
 1)
1) 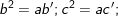
2) 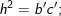
3) 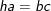
4) 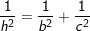
II. Định nghĩa tỉ số lượng giác của góc nhọn
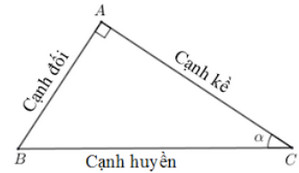
1) sinα = (cạnh đối/cạnh huyền)
2) cosα = (cạnh kề/cạnh huyền)
3) tanα = (cạnh đối/cạnh kề)
4) cotα = (cạnh kề/cạnh đối)
* Cách nhớ gợi ý:
– Để ý: Sin = Đối/Huyền; Cos = Kề/Huyền; Tan = Đối/Kề; Cot – Kề/Đối nên cách nhớ như sau: Sin Đi Học, Cos Không Hư, Tan Đoàn Kết, Cot Kết Đoàn

III. Tính chất của các các tỉ số lượng giác
• Hai góc α và β phụ nhau, khi đó:
1) sinα = cosβ
2) cosα = sinβ
3) tanα = cotβ
4) cotα = tanβ
• Cho góc nhọn α, ta có:
1) 0<sinα<1; 0<cosα<1; sin2α + cos2α = 1;
2) 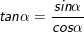
3) 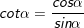
4) 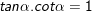
IV. Công thức, hệ thức về cạnh và góc trong tam giác vuông.
– Cho tam giác vuông như hình dưới, khi đó:
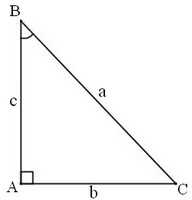
1) 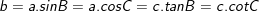
2) 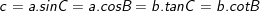
Như vậy, với việc hệ thống lại các công thức hệ thức lượng trong tam giác vuông ở trên, hy vọng sẽ giúp ích cho các em trong việc ghi nhớ và vận dụng giải các bài tập hình học lượng giác được tốt hơn. Mọi góp ý các em hãy để lại dưới phần bình luận để HayHocHoi.Vn ghi nhận và hỗ trợ.
tmdl.edu.vn. Mọi hành vi sao chép đều là gian lận!
Nguồn chia sẻ: https://tmdl.edu.vn/cong-thuc-he-thuc-luong-trong-tam-giac-vuong-ti-so-luong-giac-cua-goc-nhon/
Trang chủ: tmdl.edu.vn
Danh mục bài: Giáo dục