Công thức tính cực trị hàm số bậc bốn trùng phương cực hay & các dạng toán
Bài viết hôm nay, Trường Trung Cấp Nghề Thương Mại Du Lịch Thanh Hoá sẽ chia sẻ cùng các bạn công thức tính cực trị hàm số bậc bốn trùng phương cực hay & các dạng bài tập thường gặp. Hãy dành thời gian chia sẻ để nắm vững hơn kiến thức Toán 12 vô cùng quan trọng này bạn nhé !
I. CỰC TRỊ HÀM SỐ BẬC BỐN TRÙNG PHƯƠNG LÀ GÌ ?
Bạn đang xem bài: Công thức tính cực trị hàm số bậc bốn trùng phương cực hay & các dạng toán
1. Cực trị hàm số là gì ?

2. Cực trị hàm số bậc bốn là gì?
Cho hàm số bậc 4 : y=f(x)=ax4+bx3+cx2+dx+e với a≠0
Đạo hàm y′=4ax3+3bx2+2cx+d
Hàm số y=f(x) có thể có một hoặc ba cực trị .
Điểm cực trị là điểm mà qua đó thì đạo hàm y′ đổi dấu.
3. Cực trị hàm số bậc bốn trùng phương là gì?
Hàm số trùng phương là hàm số bậc 4 có dạng:
y=f(x)=ax4+bx2+c
Như vậy có thể coi đây là một hàm số bậc 2 với ẩn là x2
II. CÔNG THỨC TÍNH CỰC TRỊ CỦA HÀM SỐ BẬC BỐN TRÙNG PHƯƠNG CỰC HAY
Xét hàm số trùng phương f(x)=ax4+bx2+c có ba điểm cực trị tạo thành tam giác cân ABC đỉnh A
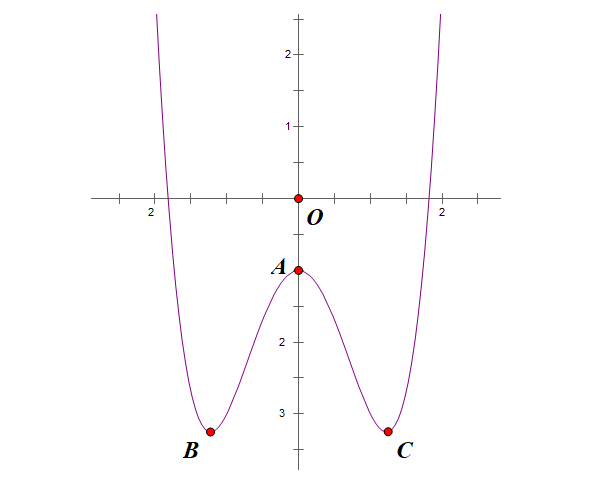
Tọa độ các đỉnh:
- A(0;c)
- B(√-b/2a;−Δ4/a)
- C(√-b/2a;−x.Δ/4a)
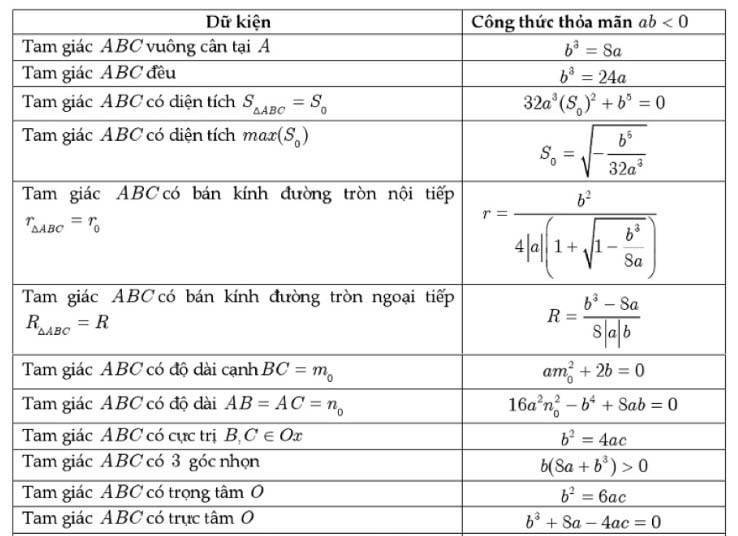
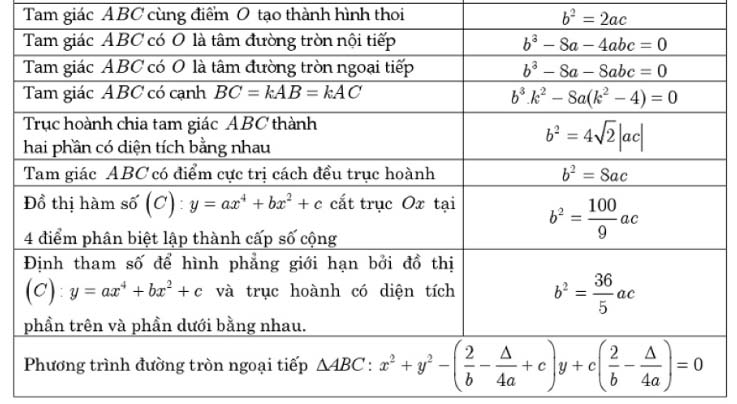
Để giải quyết nhanh các bài toán về hàm bậc 4 trùng phương trong các bài toán trắc nghiệm thì ta có các công thức sau đây
cos BACˆ=b3+8a/b3−8a
Diện tích ΔABC=b2/4|a|.√-b/2a
VÍ DỤ MINH HỌA
Ví dụ 1: Cho hàm số y = x4 – 2(m+1)x2 + m2 (1), với m là tham số thực. Tìm m để đồ thị hàm số (1) có ba điểm cực trị tạo thành ba đỉnh của một tam giác vuông.
Giải
Đạo hàm y’ = 4x3 – 4(m + 1)x.
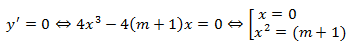
Hàm số có 3 cực trị m + 1 > 0 ⇔ m > -1
Khi đó đồ thị hàm số có 3 cực trị:
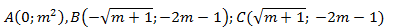
Nhận xét: A ∈ Oy, B và C đối xứng nhau qua Oy nên ∆ABC cân tại A tức là AB = AC nên tam giác chỉ có thể vuông cân tại A.
Cách 1: Gọi M là trung điểm của BC=>M(0; -2m – 1)
Do đó để tam giác ABC vuông cân ⇔ BC = 2AM (đường trung tuyến bằng nửa cạnh huyền)
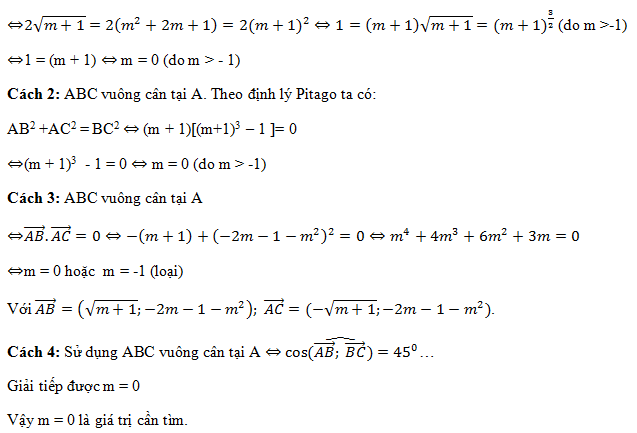
Ví dụ 2: Cho hàm số y = x4 – 2mx2 + m -1 (1), với m là tham số thực. Xác định các giá trị của tham số m để hàm số (1) có ba cực trị, đồng thời các giá trị của hàm số tạo thành một tam giác có bán kính đường tròn ngoại tiếp bằng 1.
Giải

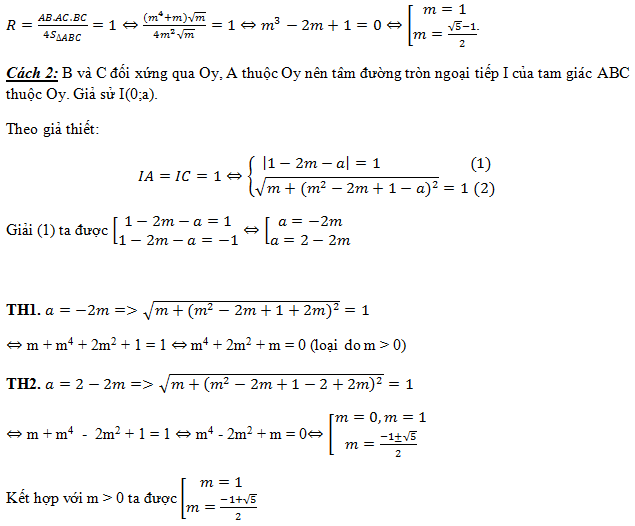
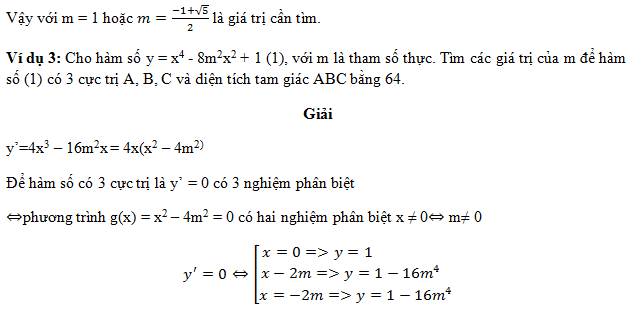
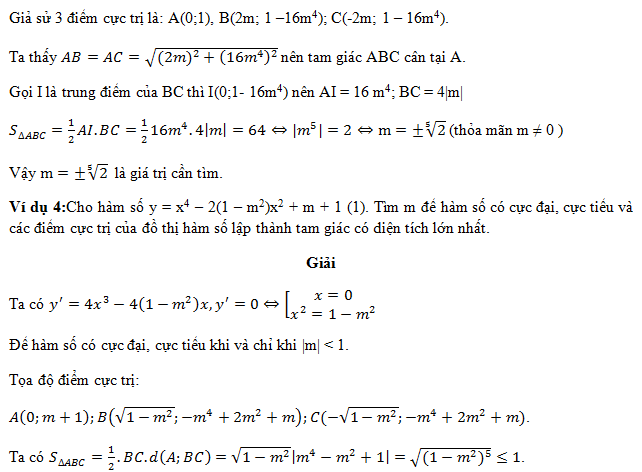
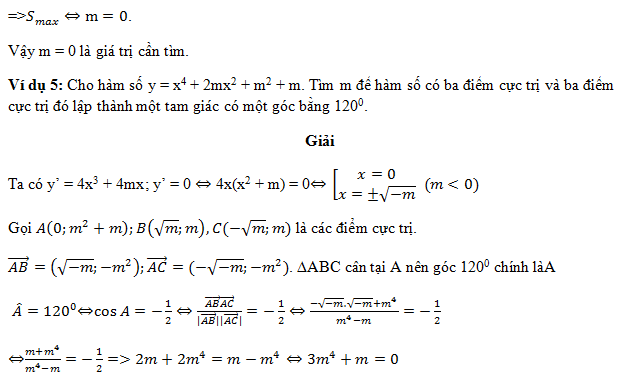
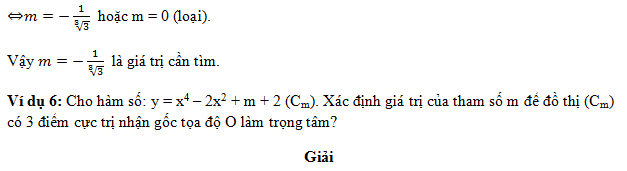
Học sinh tự giải
Vậy là các bạn vừa được tìm hiểu công thức tính cực trị hàm số bậc bốn trùng phương và nhiều dạng bài tập liên quan. Hi vọng, đây sẽ là nguồn tư liệu thiết yếu phục vụ quá trình dạy và học được tốt hơn. Xem thêm công thức tính cực trị hàm số bậc ba tại đường link này nhé !
Bản quyền bài viết thuộc Trường Trung Cấp Nghề Thương Mại Du Lịch Thanh Hoá. Mọi hành vi sao chép đều là gian lận!
Nguồn chia sẻ: https://tmdl.edu.vn/cong-thuc-tinh-cuc-tri-ham-so-bac-bon-trung-phuong-cuc-hay-cac-dang-toan/
Công thức tính cực trị hàm số bậc bốn trùng phương cực hay & các dạng toán
Bài viết hôm nay, Trường Trung Cấp Nghề Thương Mại Du Lịch Thanh Hoá sẽ chia sẻ cùng các bạn công thức tính cực trị hàm số bậc bốn trùng phương cực hay & các dạng bài tập thường gặp. Hãy dành thời gian chia sẻ để nắm vững hơn kiến thức Toán 12 vô cùng quan trọng này bạn nhé !
I. CỰC TRỊ HÀM SỐ BẬC BỐN TRÙNG PHƯƠNG LÀ GÌ ?
Bạn đang xem bài: Công thức tính cực trị hàm số bậc bốn trùng phương cực hay & các dạng toán
1. Cực trị hàm số là gì ?

2. Cực trị hàm số bậc bốn là gì?
Cho hàm số bậc 4 : y=f(x)=ax4+bx3+cx2+dx+e với a≠0
Đạo hàm y′=4ax3+3bx2+2cx+d
Hàm số y=f(x) có thể có một hoặc ba cực trị .
Điểm cực trị là điểm mà qua đó thì đạo hàm y′ đổi dấu.
3. Cực trị hàm số bậc bốn trùng phương là gì?
Hàm số trùng phương là hàm số bậc 4 có dạng:
y=f(x)=ax4+bx2+c
Như vậy có thể coi đây là một hàm số bậc 2 với ẩn là x2
II. CÔNG THỨC TÍNH CỰC TRỊ CỦA HÀM SỐ BẬC BỐN TRÙNG PHƯƠNG CỰC HAY
Xét hàm số trùng phương f(x)=ax4+bx2+c có ba điểm cực trị tạo thành tam giác cân ABC đỉnh A

Tọa độ các đỉnh:
- A(0;c)
- B(√-b/2a;−Δ4/a)
- C(√-b/2a;−x.Δ/4a)
Để giải quyết nhanh các bài toán về hàm bậc 4 trùng phương trong các bài toán trắc nghiệm thì ta có các công thức sau đây
cos BACˆ=b3+8a/b3−8a
Diện tích ΔABC=b2/4|a|.√-b/2a


VÍ DỤ MINH HỌA
Ví dụ 1: Cho hàm số y = x4 – 2(m+1)x2 + m2 (1), với m là tham số thực. Tìm m để đồ thị hàm số (1) có ba điểm cực trị tạo thành ba đỉnh của một tam giác vuông.
Giải
Đạo hàm y’ = 4x3 – 4(m + 1)x.
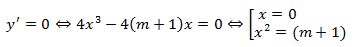
Hàm số có 3 cực trị m + 1 > 0 ⇔ m > -1
Khi đó đồ thị hàm số có 3 cực trị:
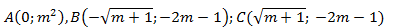
Nhận xét: A ∈ Oy, B và C đối xứng nhau qua Oy nên ∆ABC cân tại A tức là AB = AC nên tam giác chỉ có thể vuông cân tại A.
Cách 1: Gọi M là trung điểm của BC=>M(0; -2m – 1)
Do đó để tam giác ABC vuông cân ⇔ BC = 2AM (đường trung tuyến bằng nửa cạnh huyền)
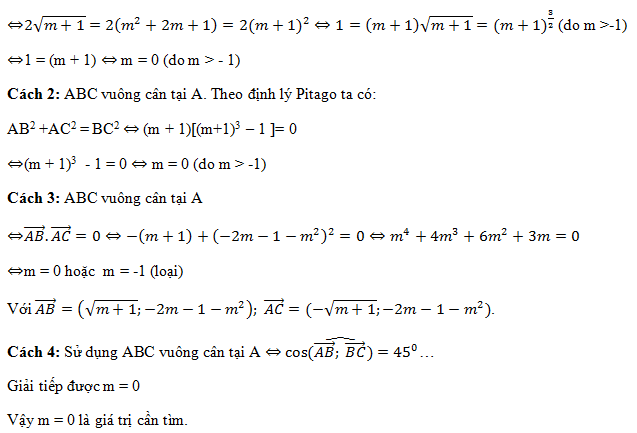
Ví dụ 2: Cho hàm số y = x4 – 2mx2 + m -1 (1), với m là tham số thực. Xác định các giá trị của tham số m để hàm số (1) có ba cực trị, đồng thời các giá trị của hàm số tạo thành một tam giác có bán kính đường tròn ngoại tiếp bằng 1.
Giải

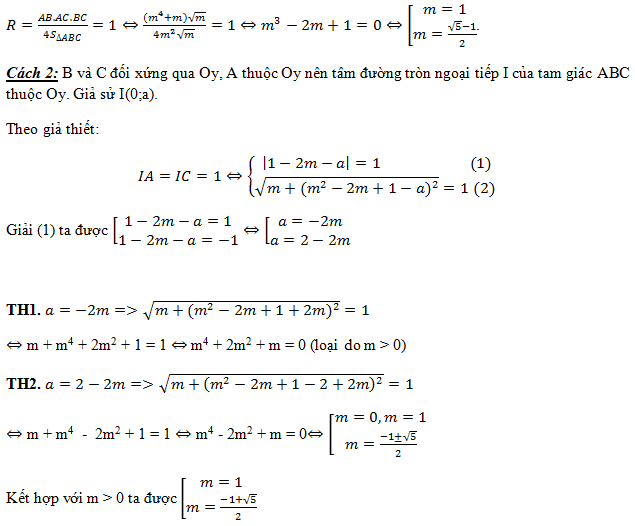
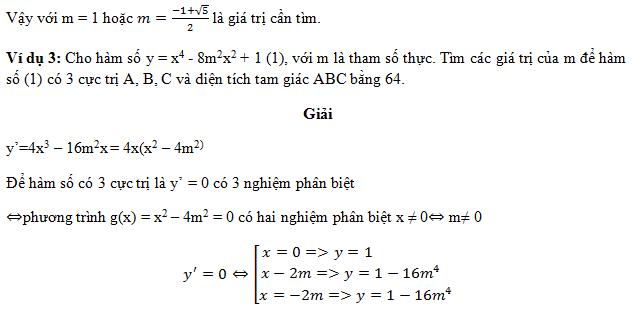
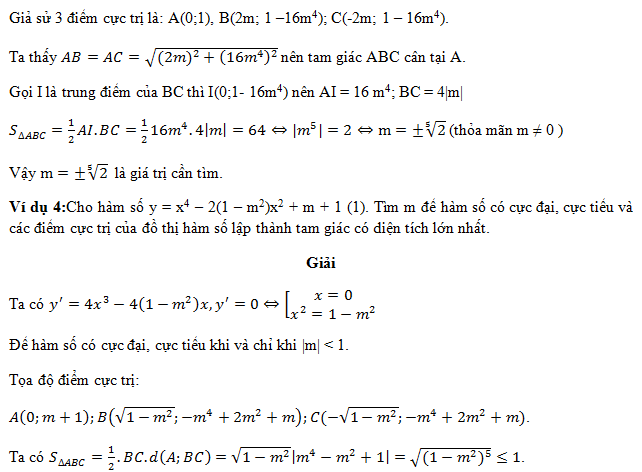
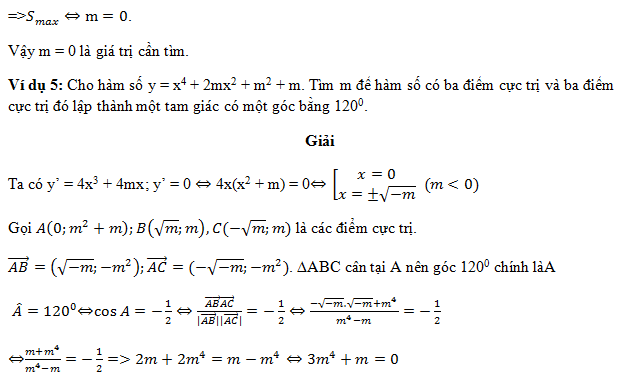
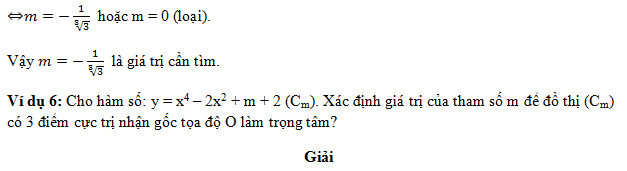
Học sinh tự giải
Vậy là các bạn vừa được tìm hiểu công thức tính cực trị hàm số bậc bốn trùng phương và nhiều dạng bài tập liên quan. Hi vọng, đây sẽ là nguồn tư liệu thiết yếu phục vụ quá trình dạy và học được tốt hơn. Xem thêm công thức tính cực trị hàm số bậc ba tại đường link này nhé !
Bản quyền bài viết thuộc Trường Trung Cấp Nghề Thương Mại Du Lịch Thanh Hoá. Mọi hành vi sao chép đều là gian lận!
Nguồn chia sẻ: https://tmdl.edu.vn/cong-thuc-tinh-cuc-tri-ham-so-bac-bon-trung-phuong-cuc-hay-cac-dang-toan/
Trang chủ: tmdl.edu.vn
Danh mục bài: Giáo dục