Công thức tính diện tích hình trụ: diện tích xung quanh & diện tích toàn phần

Ở bài viết trước, Trường Trung Cấp Nghề Thương Mại Du Lịch Thanh Hoá đã giới thiệu đến quý thầy cô và các bạn học sinh công thức tính thể tích khối trụ. Bài viết hôm nay, chúng tôi sẽ tiếp tục giới thiệu Công thức tính diện tích hình trụ: công thức tính diện tích xung quanh hình trụ và công thức tính diện tích toàn phần hình trụ. Bên cạnh đó, chúng tôi sẽ cung cấp thêm các dạng bài tập vận dụng để bạn nắm chắc hơn nội dung bài. Cùng tìm hiểu nhé !

I. LÝ THUYẾT CHUNG

Bạn đang xem bài: Công thức tính diện tích hình trụ: diện tích xung quanh & diện tích toàn phần

1. Hình trụ là gì?

Khi quay hình chữ nhật ABCD một vòng quanh cạnh CD cố định ta thu được một hình trụ.

– Hai đáy là hình tròn bằng nhau và nằm trên hai mặt phẳng song song.

– DC là trục của hình trụ.

– Các đường sinh của hình trụ( chẳng hạn EF) vuông góc với hai mặt đáy.

Độ dài đường sinh cũng là độ dài đường cao của hình trụ.

Hình trụ được sử dụng khá phổ biến trong các bài toán hình học từ căn bản đến phức tạp, trong đó công thức tính diện tích, thể tích hình trụ thường được sử dụng khác phổ biến trong việc tính một không gian nhất định bị chiếm giữ bởi một hình trụ.

Bên cạnh đó, công thức tính diện tích, thể tích hình trụ cũng được áp dụng trong các dạng bài toán phức hợp thêm cách tính thể tích hình lập phương hay diện tích hình chữ nhật. Cùng tham khảo công thức tính thể tích hình trụ và các ví dụ trực quan nhất trong cách tính diện tích, thể tích hình trụ.

jtn2znxruj9kwdkt3sz0qpkwysbgiwgsfn7skrif 1 3

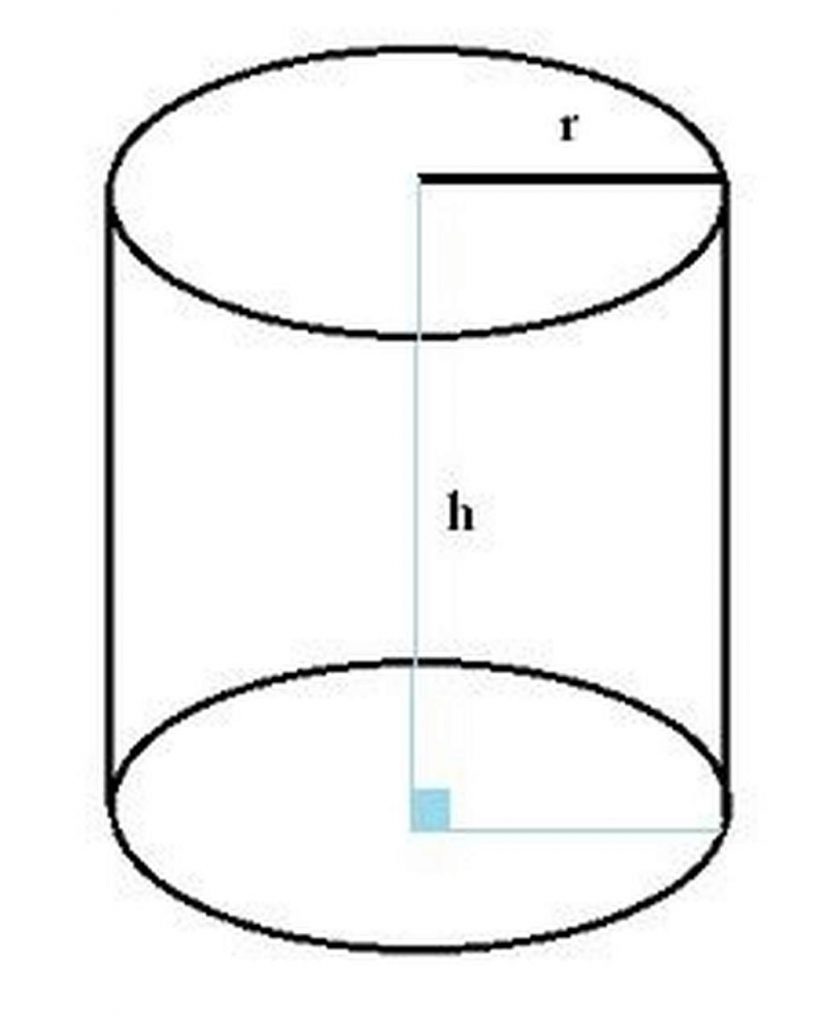
2. Diện tích hình trụ là gì ?

Diện tích hình trụ là toàn bộ không gian chiếm giữ bằng cách tính tổng diện tích xung quanh và diện tích hai đáy. Trong khi đó, diện tích toàn phần hình trụ là diện tích của mặt xung quanh hình trụ, không gồm diện tích hai đáy.

II. CÔNG THỨC TÍNH DIỆN TÍCH HÌNH TRỤ

1. Công thức tính diện tích xung quanh của hình trụ

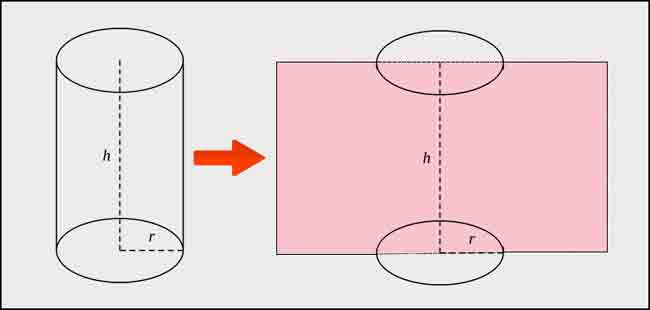
Diện tích xung quanh hình trụ tròn chỉ bao gồm diện tích mặt xung quanh, bao quanh hình trụ tròn, không gồm diện tích hai đáy.

Công thức tính diện tích xung quanh bằng chu vi đường tròn đáy nhân với chiều cao.

S_{xung quanh} = 2 x π x r x h

Trong đó:

+ r: bán kính hình trụ

+ h: chiều cao nối từ đáy tới đỉnh hình trụ

fkrgcxphl0ygxn3xvpfc4ziymfsoikduglzrsd4s 1

Ví dụ: Mô hình của một cái lọ thí nghiệm dạng hình trụ (không nắp) có bán kính đường tròn đáy 14cm,chiều cao 10cm. Tìm diện tích xung quanh cộng với diện tích một đáy

Lời giải:

2. Công thức tính diện tích toàn phần của hình trụ

Diện tích toàn phần của hình trụ được tính là độ lớn của toàn bộ không gian hình chiếm giữ, bao gồm cả diện tích xung quanh và diện tích hai đáy tròn.

Công thức: Công thức tính diện tích toàn phần bằng diện tích xung quanh cộng với diện tích của 2 đáy.

S _{toàn phần} = 2 x π x r² + 2 x π x r x h = 2 π x r x (r + h)

Trong đó:

+ r: bán kính hình trụ

+ 2 x π x r x h: diện tích xung quanh hình trụ

+ 2 x π x r²: diện tích của hai đáy

Ví dụ:

Một hình trụ tròn có bán kính đáy r = 4 cm, chiều cao h = 6 cm. Tính diện tích toàn phần hình trụ đứng.

Hướng dẫn giải: S_tp = S_xq + 2.S_đáy= 2.π.r² + 2.π.r.h = 2.π.4² + 2.π.4.6 = 32π + 48π = 80π (cm²).

III. BÀI TẬP VỀ DIỆN TÍCH HÌNH TRỤ

Bài 1:

Một bóng đèn huỳnh quang dài 1,2m, đường kính của đường tròn đáy là 4cm, được đặt khít vào một ống giấy cứng dạng hình hộp. Tính diện tích phần giấy cứng dùng để làm một hộp.

Lời giải:

Diện tích phần giấy cứng cần tính chính là diện tích xung quanh của một hình hộp có đáy là hình vuông cạnh 4cm, chiều cao 1,2m = 120cm.

Diện tích xung quanh của hình hộp chính là diện tích bốn hình chữ nhật bằng nhau với chiều dài là 120 cm và chiều rộng 4cm::

S_xq= 4.4.120 = 1920 cm²

^{Đáp số: 1920 cm2}

Bài 2: Tính diện tích toàn phần của hình trụ, có độ dài đường tròn đáy là 10cm, khoảng cách giữa 2 đáy là 6cm.

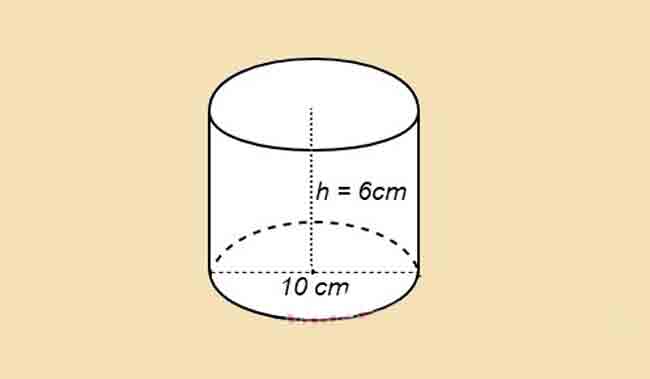
Giải

Theo đề bài ta có: h = 6cm; 2r = 10cm => r = 5cm.

Áp dụng công thức tính diện tích toàn phần hình trụ:

Stp=2πr(r+h)=2π.5(5+6)=110π(cm2)

=> Vậy diện tích toàn phần của hình trụ là 110π(cm2)

Bài 3: Tính diện tích toàn phần của hình trụ có chiều cao là 7cm và diện tích xung quanh bằng 310 (cm2)

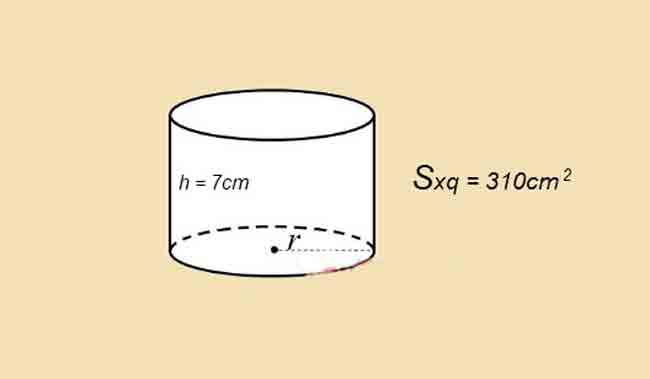
Giải

Theo đề bài ta có: h = 7; Sxq=310

Áp dụng công thức tính diện tích xung quanh Sxq=2πrh

=> r=Sxq2πrh=3102π.7≈7cm

Vậy S_đ=πr2=π.72=49π≈154cm2

=> Diện tích toàn phần của hình trụ: S_tp=2.Sđ+Sxq=2.154+310=618cm2

Bài 4: Một hình trụ có chu vi đáy bằng 20 cm, diện tích xung quanh bằng 14 cm². Tính chiều cao của hình trụ và thể tích của hình trụ.

Giải:

Diện tích xung quanh của hình trụ: Sxq = chu vi đáy x chiều cao = 2 x π x r x h = 20 x h = 14

→ h = 0,7 (cm)

Chu vi đáy bằng 20cm → 2 x π x r = 20 → r ~ 3,18 cm

Thể tích của hình trụ: V = π x r² x h ~ 219,91 cm³

Bài 5: Một hình trụ có diện tích toàn phần gấp 2 lần diện tích xung quanh biết bán kính đáy hình trụ là 6cm. Tính thể tích hình trụ.

Giải:

Diện tích toàn phần gấp 2 lần diện tích xung quanh: Stp = 2Sxq

→ 2 x 2 x π x r x h = 2 x π x r x (r + h) → 2h = 6 + h → h = 6 (cm)

Thể tích của hình trụ: V = π x r² x h ~ 678,58 cm³

Bài 6: Một hình trụ có bán kính đáy là 7cm, diện tích xung quanh bằng 352cm2.

Khi đó, chiều cao của hình trụ là:

(A) 3,2 cm; (B) 4,6cm; (C) 1,8 cm

(D) 2,1cm; (E) Một kết quả khác

Hãy chọn kết quả đúng.

Giải:

bai tap tinh dien tich hinh tru lop 9 2

Bài 7: Chiều cao của một hình trụ bằng bán kính đường tròn đáy. Diện tích xung quanh của hình trụ 314 cm2.

Hãy tính bán kính đường tròn đáy và thể tích hình trụ (làm tròn kết quả đến chữ số thập phân thứ hai).

Giải:

Diện tích xung quanh hình trụ bằng 314cm2

⇔ 2.π.r.h = 314

Mà r = h

⇒ 2πr²= 314

⇒ r² ≈ 50

⇒ r ≈ 7,07 (cm)

Thể tích hình trụ: V = π.r².h = π.r³ ≈ 1109,65 (cm3).

Bài 8: Một bóng đèn huỳnh quang dài 1,2m, đường kính của đường tròn đáy là 4cm, được đặt khít vào một ống giấy cứng dạng hình hộp (h.82). Tính diện tích phần giấy cứng dùng để làm một hộp.

(Hộp hở hai đầu, không tính lề và mép dán).

bai tap tinh dien tich hinh tru lop 9 5

Hình 82

Giải:

Diện tích phần giấy cứng cần tính chính là diện tích xung quanh của một hình hộp có đáy là hình vuông cạnh 4cm, chiều cao 1,2m = 120cm.

Diện tích xung quanh của hình hộp chính là diện tích bốn hình chữ nhật bằng nhau với chiều dài là 120 cm và chiều rộng 4cm::

Sxq= 4.4.120 = 1920 cm2

Bài 9: Hình 83 là một hình trụ cùng với hình khai triển của nó kèm theo kích thước.

bai tap tinh dien tich hinh tru lop 9 6

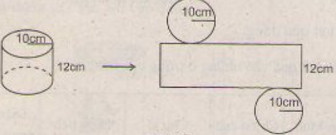
Hãy điền vào các chỗ … và các ô trống những cụm từ hoặc các số cần thiết.

bai tap tinh dien tich hinh tru lop 9 7

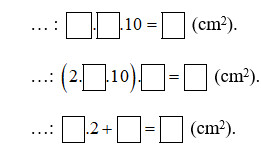
Giải:

Điền vào chỗ trống như sau:

Diện tích đáy: 10.π.10 = 100π (cm2).

Diện tích xung quanh: (2.π.10).12 = 240π (cm2).

Diện tích toàn phần: 100π.2 + 240π = 440π (cm2).

Bài 10 : Hãy tính:

a) Diện tích xung quanh của một hình trụ có chu vi hình tròn đáy là 13cm và chiều cao là 3cm.

b) Thể tích của hình trụ có bán kính đường tròn đáy là 5mm và chiều cao là 8mm.

Giải:

Ta có : C = 13cm, h = 3cm

Diện tích xung quanh của hình trụ là :

Sxq = 2πr.h = C.h = 13.3 = 39 (cm2)

b) Ta có : r = 5mm, h = 8mm

Thể tích hình trụ là :

V = πr².h = π. 5².8 = 200π ≈ 628 (mm3)

Bài 11: Diện tích xung quanh của một hình trụ là 10m2 và diện tích toàn phần của nó là 14m2.Hãy tính bán kính của đường tròn đáy và chiều cao của hình trụ (lấy π =3,14 ; làm tròn kết quả đến chữ số thập phân thứ 2)

Giải:

bai tap tinh dien tich hinh tru lop 9 15

Trên đây, Trường Trung Cấp Nghề Thương Mại Du Lịch Thanh Hoá đã giới thiệu đến quý thầy cô và các bạn học sinh Công thức tính diện tích hình trụ: công thức tính diện tích xung quanh hình trụ và công thức tính diện tích toàn phần hình trụ cùng nhiều bài tập vận dụng có đáp án. Hi vọng, đây là nguồn tư liệu quý giá giúp các bạn dạy và học tốt hơn. Xem thêm công thức tính thể tích khối trụ tại đường link này nữa bạn nhé !

Bản quyền bài viết thuộc Trường Trung Cấp Nghề Thương Mại Du Lịch Thanh Hoá. Mọi hành vi sao chép đều là gian lận!
Nguồn chia sẻ: https://tmdl.edu.vn/cong-thuc-tinh-dien-tich-hinh-tru-dien-tich-xung-quanh-dien-tich-toan-phan/

Trang chủ: tmdl.edu.vn
Danh mục bài: Giáo dục

Lương Sinh20 Tháng Hai, 2023