Công thức tính góc giữa hai đường thẳng trong mặt phẳng và trong không gian
Bài viết hôm nay, Trường Trung Cấp Nghề Thương Mại Du Lịch Thanh Hoá sẽ giới thiệu đến quý bạn đọc công thức tính góc giữa hai đường thẳng trong mặt phẳng và trong không gian cực chi tiết. Các bạn dành thời gian chia sẻ để có thêm nguồn tư liệu quý phục vụ quá trình dạy và học tốt hơn nhé !
I. LÝ THUYẾT CẦN GHI NHỚ
Bạn đang xem bài: Công thức tính góc giữa hai đường thẳng trong mặt phẳng và trong không gian
1. Góc giữa hai đường thẳng là gì?
Hai đường thẳng trong không gian gồm 4 vị trí tương đối là cắt nhau, song song, trùng nhau và chéo nhau như sau:
- Khi hai đường thằng song song hoặc trùng nhau thì góc hai đường thẳng bằng 0o
- Khi hai đường thẳng cắt nhau sẽ tạo thành 2 góc đối đỉnh hay còn gọi là 4 góc. Lúc này ta chọn góc không tù là góc giữa hai đường thẳng
- Khi hai đường thẳng chéo nhau, ta chọn một điểm bất kỳ trong không gian. Từ đó dựng lần lượt 2 đường thẳng song song với hai đường thẳng đã cho. Chính vì vậy, hai đường thẳng mới này cắt nhau và góc của chúng chính là góc giữa 2 đường thẳng đã được cho (Chú ý việc chọn điểm không ảnh hưởng đến số đo của góc).
2. Góc giữa hai mặt phẳng là gì?
Góc giữa 2 mặt phẳng là góc được tạo bởi hai đường thẳng lần lượt vuông góc với hai mặt phẳng đó.
Trong không gian 3 chiều, góc giữa 2 mặt phẳng còn được gọi là ‘góc khối’, là phần không gian bị giới hạn bởi 2 mặt phẳng. Góc giữa 2 mặt phẳng được đo bằng góc giữa 2 đường thẳng trên mặt 2 phẳng có cùng trực giao với giao tuyến của 2 mặt phẳng.
Tính chất: Từ định nghĩa trên ta có:
- Góc giữa 2 mặt phẳng song song bằng 0 độ,
- Góc giữa 2 mặt phẳng trùng nhau bằng 0 độ.
II. CÔNG THỨC TÍNH GÓC GIỮA HAI ĐƯỜNG THẲNG TRONG MẶT PHẲNG VÀ TRONG KHÔNG GIAN

1. Công thức tính
– Cho hai đường thẳng d, d’ có vectơ chỉ phương 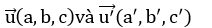
Góc φ giữa hai đường thẳng được tính theo công thức:
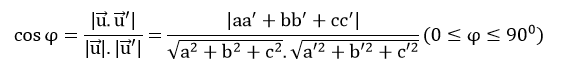
– Cho đường thẳng d có vectơ chỉ phương 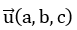 và mặt phẳng (P) có vectơ pháp tuyến
và mặt phẳng (P) có vectơ pháp tuyến 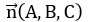
Góc φ giữa đường thẳng d và mặt phẳng (P) được tính theo công thức:
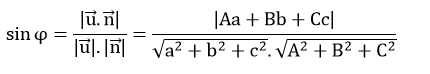
2. Ví dụ minh họa
Ví dụ 1:
Tính cosin góc giữa đường thẳng d với trục Ox biết 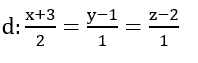
A. 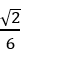
B. 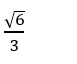
C. 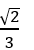
D. 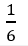
Hướng dẫn giải
Đường thẳng d có vecto chỉ phương 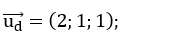
Trục Ox có vecto chỉ phương 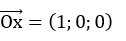
Cosin góc giữa d và Ox là:
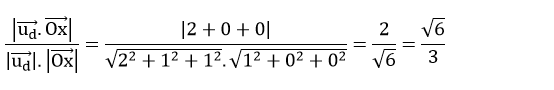
Chọn B.
Ví dụ: 2
Trong không gian với hệ tọa độ Oxyz; gọi đường thẳng d đi qua A( -1; 0; -1), cắt 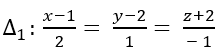 , sao cho cosin góc giữa d và
, sao cho cosin góc giữa d và 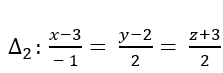 là nhỏ nhất. Phương trình đường thẳng d là
là nhỏ nhất. Phương trình đường thẳng d là
A. 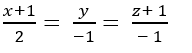
B. 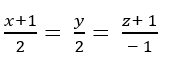
C. 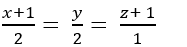
D. Đáp án khác
Hướng dẫn giải
Gọi giao điểm của đường thẳng d và Δ1 là M( 1+ 2t; 2+ t; -2- t)
Đường thẳng d có vectơ chỉ phương 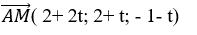
Đường thẳng Δ2 có vectơ chỉ phương 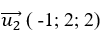
=> cosin góc giữa hai đường thẳng d và Δ2 là:
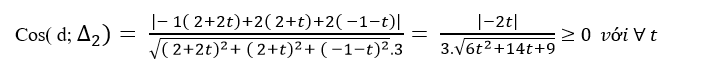
=> cosin góc giữa hai đường thẳng d và Δ2 là 0 khi t= 0.
Khi đó; M( 1; 2; – 2) và 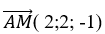
Vậy phương trình đường thẳng d là: 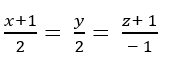
Chọn B.
III. CÁC DẠNG BÀI TẬP THƯỜNG GẶP
Bài 1:
Cho đường thẳng 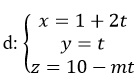 và mặt phẳng (P): 4x- 4y+ 2z- 9= 0. Xác định m để
và mặt phẳng (P): 4x- 4y+ 2z- 9= 0. Xác định m để 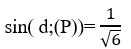
A. m= 1
B.m= – 1
C. m= – 2
D. m= -1 hoặc m= -7
Hướng dẫn giải
+ Đường thẳng d có vecto chỉ phương 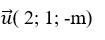
Mặt phẳng (P) có vecto pháp tuyến 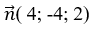
=> Sin góc tạo bởi đường thẳng d và mặt phẳng (P) là:
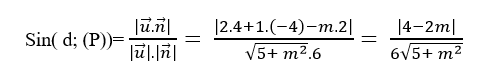
Theo giả thiết ta có: 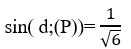
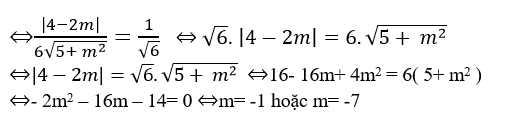
Chọn D.
Bài 2:
Cho đường thẳng 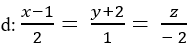 ; điểm A( 2; 0; 0); B (0; 1; 0) và C( 0;0;- 3).Xác định sin góc giữa đường thẳng d và mặt phẳng (ABC) ?
; điểm A( 2; 0; 0); B (0; 1; 0) và C( 0;0;- 3).Xác định sin góc giữa đường thẳng d và mặt phẳng (ABC) ?
A. 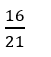
B. 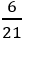
C. 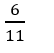
D. Đáp án khác
Hướng dẫn giải
+ Phương trình mặt phẳng (ABC): 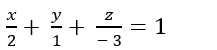
Hay ( ABC): 3x + 6y – 2z – 6= 0
Mặt phẳng (ABC) có vecto pháp tuyến 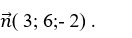 .
.
+ Đường thẳng d có vecto chỉ phương 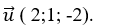 .
.
=> Sin góc giữa đường thẳng d và mặt phẳng (P) là:
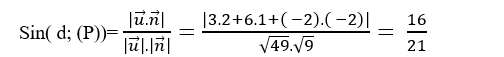
Chọn A.
Bài 3:
Cho bốn điểm A( 1; 0;1) ; B( -1; 2; 1); C( -1; 2; 1) và D( 0; 4; 2). Xác định cosin góc giữa hai đường thẳng AB và CD?
A. 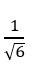
B. 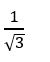
C. 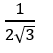
D. Đáp án khác
Hướng dẫn giải
+ Đường thẳng AB có vecto chỉ phương 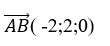
+ Đường thẳng CD có vecto chỉ phương 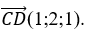 .
.
=> Cosin góc giữa hai đường thẳng AB và CD là:
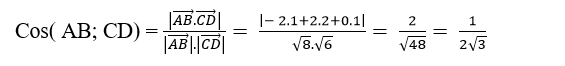
Chọn C.
Bài 4:
Cho đường thẳng 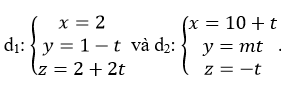 . Xác định m để cosin góc giữa hai đường thẳng đã cho là:
. Xác định m để cosin góc giữa hai đường thẳng đã cho là: 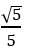
A. m= 2
B. m = – 4
C. m= (- 1)/2
D. m= 1
Hướng dẫn giải
Đường thẳng d1 có vecto chỉ phương 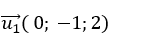
Đường thẳng d2 có vecto chỉ phương 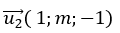
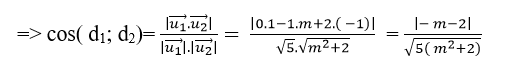
Để cosin góc giữa hai đường thẳng đã cho là:
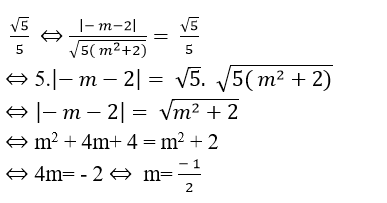
Chọn C.
Bài 5:
Cho đường thẳng 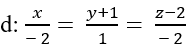 và mặt phẳng (P): x+ my- z+ 100= 0. Xác định m để cosin góc giữa đường thẳng d và mặt phẳng (P) là
và mặt phẳng (P): x+ my- z+ 100= 0. Xác định m để cosin góc giữa đường thẳng d và mặt phẳng (P) là 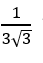 ?
?
A. m= ± 1
B.m= ± 2
C. m= 0
D. m= ± 3
Hướng dẫn giải
Đường thẳng d có vecto chỉ phương 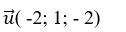
Mặt phẳng (P) có vecto pháp tuyến 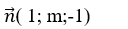
=> Sin góc tạo bởi đường thẳng d và mặt phẳng (P) là:
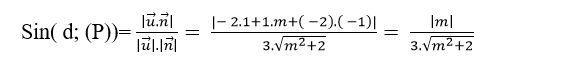
Theo giả thiết ta có:
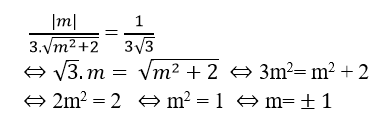
Chọn A.
Bài 6:
Tính góc giữa 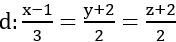 và d’ là giao tuyến của hai mặt phẳng: (P): x + 2y – z + 1 = 0 và (Q): 2x + 3z – 2 = 0?
và d’ là giao tuyến của hai mặt phẳng: (P): x + 2y – z + 1 = 0 và (Q): 2x + 3z – 2 = 0?
A. 30o
B. 45o
C. 60o
D. 90o
Hướng dẫn giải
Hai mặt phẳng (P)và (Q) có vecto pháp tuyến là: 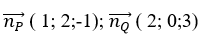
d’ là giao tuyến của (P) và (Q) nên vectơ chỉ phương của d’ là
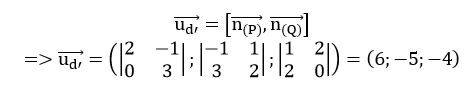
Đường thẳng d có vecto chỉ phương 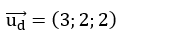
Cosin góc giữa d và d’ là:
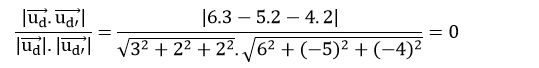
=> góc giữa d và d’ bằng 90o.
Chọn D.
Bài 7:
Tính sin góc giữa đường thẳng d và mặt phẳng (P) biết 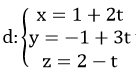 và (P): 2x – y + 2z – 1 = 0?
và (P): 2x – y + 2z – 1 = 0?
A. 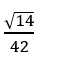
B. 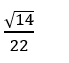
C. 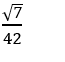
D. Đáp án khác
Hướng dẫn giải
Đường thẳng d có vecto chỉ phương 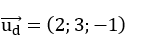
Mặt phẳng (P) có vecto pháp tuyến  nên sin góc giữa d và (P) là:
nên sin góc giữa d và (P) là:
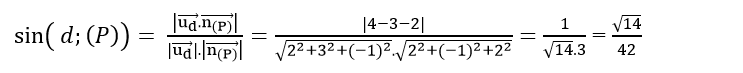
Chọn A.
Bài 8:
Trong không gian với hệ tọa độ Oxyz; gọi d đi qua điểm A( 1; -1; 2) , song song với (P): 2x- y- z+ 3= 0 , đồng thời tạo với đường thẳng 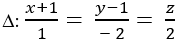 một góc α sao cho cosα đạt giá trị nhỏ nhât. Phương trình đường thẳng d là.
một góc α sao cho cosα đạt giá trị nhỏ nhât. Phương trình đường thẳng d là.
A. 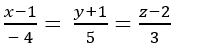
B. 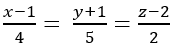
C.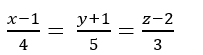
D. 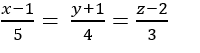
+ Đường thẳng Δ có vectơ chỉ phương 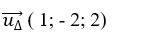
Đường thẳng d có vectơ chỉ phương 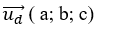
Mặt phẳng (P) có vectơ pháp tuyến 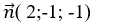
+ Vì d// (P) nên hai vecto ud→ và n→ vuông góc với nhau.
=> ud→.n→= 0 ⇔ 2a- b- c= 0 ⇔ c= 2a- b
+ Cosin góc tạo bởi đường thẳng d và Δ là:
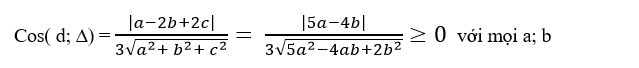
=> cosin góc tạo bởi hai đường thẳng d và Δ đạt giá trị nhỉ nhất là 0 khi 5a- 4b= 0
Chọn a= 4 => b= 5 và c= 3
+ Đường thẳng d đi qua điểm A (1; -1; 2) và nhận vecto 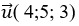 làm vecto chỉ phương
làm vecto chỉ phương
=> Phương trình d: 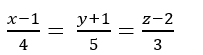
Chọn C.
Bài 9:
Trong không gian với hệ tọa độ Oxyz; cho đường thẳng 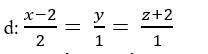 mặt phẳng (P): 2x- y- z+ 5= 0 và M( 1; -1; 0). Đường thẳng Δ đi qua điểm M, cắt d và tạo với mặt phẳng (P) một góc thỏa mãn sin (Δ; (P))= 0,5
mặt phẳng (P): 2x- y- z+ 5= 0 và M( 1; -1; 0). Đường thẳng Δ đi qua điểm M, cắt d và tạo với mặt phẳng (P) một góc thỏa mãn sin (Δ; (P))= 0,5
A. 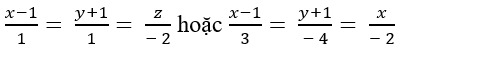
B.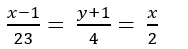
C. 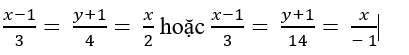
D. 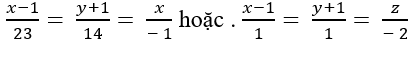
Bài 10:
Trong không gian Oxyz, cho điểm A( -2; 0; 0), đường thẳng d qua điểm A cắt và tạo với trục Oy góc 45o. Đường thẳng d có vecto chỉ phương là:
A. ( 2;2; 1) hoặc ( 2;- 2; 1)
B . ( 2; -1;0) hoặc ( 2; 1;0)
C. ( 1;2; 0) hoặc ( – 2; 1;0)
D. ( 2; 2; 0) hoặc ( 2; -2; 0)
Gọi giao điểm của đường thẳng d và trục Oy là M( 0; m;0)
Trục Oy có vectơ chỉ phương là 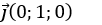
Đường thẳng d có vecto chỉ phương 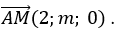 .
.
Góc giữa đường thẳng d và trục Oy là 45o nên ta có:
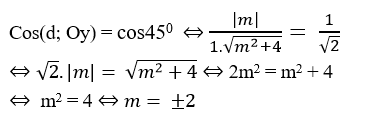
+ Với m= 2 đường thẳng d có vecto chỉ phương 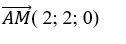
+Với m = -2 đường thẳng d có vecto chỉ phương 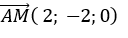
Chọn D.
Vậy là Trường Trung Cấp Nghề Thương Mại Du Lịch Thanh Hoá đã giới thiệu đến các bạn công thức tính góc giữa hai đường thẳng trong mặt phẳng và trong không gian cực chi tiết. Hi vọng, đây sẽ là nguồn tư liệu thiết yếu giúp các bạn dạy và học tốt hơn. Xem thêm công thức tính góc giữa hai vectơ tại đường link này bạn nhé !
Bản quyền bài viết thuộc Trường Trung Cấp Nghề Thương Mại Du Lịch Thanh Hoá. Mọi hành vi sao chép đều là gian lận!
Nguồn chia sẻ: https://tmdl.edu.vn https://tmdl.edu.vn/cong-thuc-tinh-goc-giua-hai-duong-thang-trong-mat-phang-va-trong-khong-gian/
Trang chủ: tmdl.edu.vn
Danh mục bài: Giáo dục





