Hướng dẫn các bước khảo sát và vẽ đồ thị hàm số bậc 4 trùng phương
Ở bài viết trước, Trường Trung Cấp Nghề Thương Mại Du Lịch Thanh Hoá đã giới thiệu đến thầy cô cùng các bạn học sinh các bước khảo sát và vẽ đồ thị hàm số bậc ba. Tiếp nối mạch kiến thức đó, hôm nay chúng tôi sẽ hướng dẫn các bước khảo sát và vẽ đồ thị hàm số bậc 4 trùng phương. Chia sẻ để nắm chắc hơn chuyên đề Đại số quan trọng này nhé !
I. LÝ THUYẾT CHUNG
Bạn đang xem bài: Hướng dẫn các bước khảo sát và vẽ đồ thị hàm số bậc 4 trùng phương
1. Cực trị của hàm bậc 4 là gì?
Cho hàm số bậc 4 : y=f(x)=ax4+bx3+cx2+dx+e với a≠0
Đạo hàm y′=4ax3+3bx2+2cx+d
Hàm số y=f(x) có thể có một hoặc ba cực trị .
Điểm cực trị là điểm mà qua đó thì đạo hàm y′ đổi dấu
2. Số điểm cực trị của hàm bậc 4
Xét đạo hàm y′=4ax3+3bx2+3cx+d
- Nếu y′=0 có đúng 1 nghiệm thì hàm số y=f(x) có đúng 1 cực trị (có thể là cực đại hoặc cực tiểu).
- Nếu y′=0 có 2 nghiệm (gồm 1 nghiệm đơn , 1 nghiệm kép) thì hàm số y=f(x) có đúng 1 cực trị (có thể là cực đại hoặc cực tiểu).
- Nếu y′=0 có 3 nghiệm phân biệt thì hàm số y=f(x) có 3 cực trị (gồm cả cực đại và cực tiểu).
3. Hàm số trùng phương là gì ?
Hàm số trùng phương là hàm số bậc 4 có dạng:
y=f(x)=ax4+bx2+c
Như vậy có thể coi đây là một hàm số bậc 2 với ẩn là x2
4. Điều kiện cực trị của hàm bậc 4 trùng phương

II. CÁC BƯỚC KHẢO SÁT VÀ VẼ ĐỒ THỊ HÀM SỐ BẬC 4 TRÙNG PHƯƠNG
1. Cách khảo sát và vẽ đồ thị hàm số bậc 4 trùng phương
Để khảo sát và vẽ đồ thị hàm số bậc 4 trùng phương ta thực hiện các bước sau đây:
Bước 1: Tìm tập xác định. D=R
Bước 2: Xét sự biến thiên
- Xét chiều biến thiên của hàm số
+ Tính đạo hàm y’ = 4ax3 + 2bx
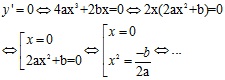
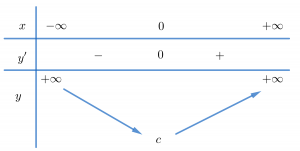
+ Xét dấu đạo hàm y’ và suy ra chiều biến thiên của hàm số.
- Tìm cực trị
- Tìm các giới hạn tại vô cực ( x →± ∞). (Hàm trùng phương không có TCĐ và TCN.)
- Lập bảng biến thiên
Thể hiện đầy đủ và chính xác các giá trị trên bảng biến thiên
Bước 3: Vẽ đồ thị
– Giao của đồ thị với trục Oy: x=0 =>y= c => (0;c)
– Giao của đồ thị với trục Ox:
– Các điểm CĐ; CT nếu có.
(Chú ý: giải phương trình trùng phương- các bạn bấm máy tính như giải pt bậc 2 nhưng chỉ lấy nghiệm không âm, sau đó giải để tìm ra x)
– Lấy thêm một số điểm (nếu cần)- (điều này làm sau khi hình dung hình dạng của đồ thị. Thiếu bên nào học sinh lấy điểm phía bên đó, không lấy tùy tiện mất thời gian.)
– Nhận xét về đặc trưng của đồ thị. Ta có: Nên đồ thị hàm số đã cho là hàm số chẵn. Đồ thị của nó nhận Oy làm trục đối xứng..
2. Các trường hợp biến thiên của đồ thị hàm số bậc 4
Trường hợp 1. a>0, b≥0
Hàm số đồng biến trên khoảng (0;+∞) và nghịch biến trên (−∞;0).
Trường hợp này đồ thị hàm trùng phương có dạng gần giống đồ thị hàm số bậc 2.

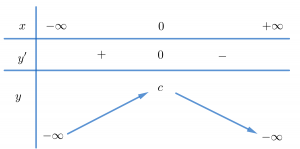
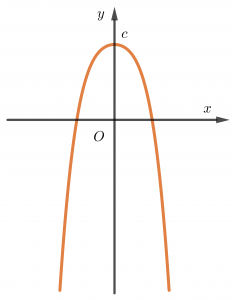
Trường hợp 2. a<0, b≤0
Hàm số nghịch biến trên khoảng (0;+∞) và đồng biến trên (−∞;0).
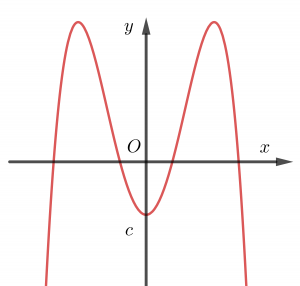
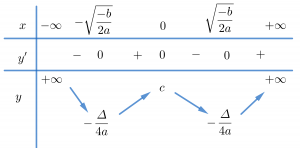
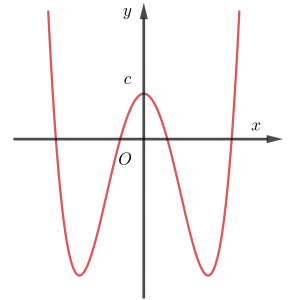
Trường hợp 3. a>0, b<0
Chúng ta thường nhớ hình dáng bảng biến thiên trường hợp này giống chữ W.
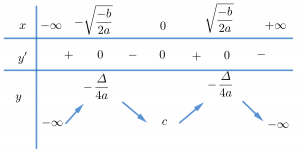
Trường hợp 4. a<0, b>0
Chúng ta thường nhớ hình dáng bảng biến thiên trường hợp này giống chữ M.
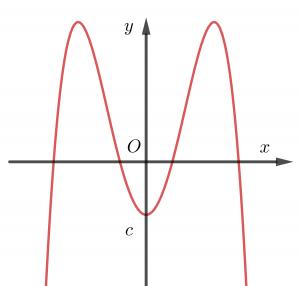
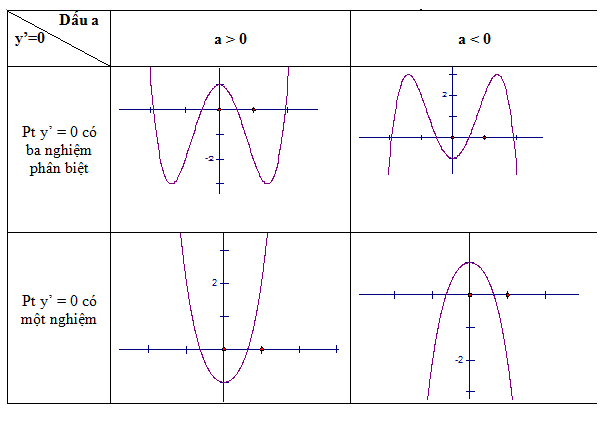
3. Các dạng đồ thị hàm số bậc 4 trùng phương: y = ax4 + bx2 + c (a≠0)
III. BÀI TẬP VỀ ĐỒ THỊ HÀM SỐ BẬC 4 TRÙNG PHƯƠNG
1. Bài tập có lời giải
Bài 1:
Cho hàm số y = x4 – 2x2 – 1 có đồ thị (C).
a. Khảo sát sự biến thiên và vẽ đồ thị (C) của hàm số;
b. Dùng đồ thị (C), hãy biện luận theo m số nghiệm thực của phương trình x4 – 2x2 – 1= m (*)
a. Khảo sát sự biến thiên và vẽ đồ thị:
* Tập xác định: D= R.
* Chiều biến thiên :
Ta có : y’= 4x3 – 4x = 4x (x2 -1)
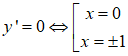
Giới hạn của hàm số tại vô cực: 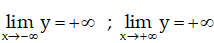
o Bảng biến thiên :
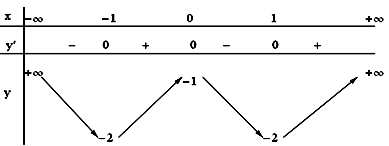
Hàm số nghịch biến trên các khoảng 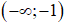 và (0; 1), đồng biến trên các khoảng (-1; 0) và
và (0; 1), đồng biến trên các khoảng (-1; 0) và 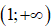
Hàm số đạt cực đại tại điểm x= 0 ; giá trị cực đại của hàm số là y(0) = – 1.
Hàm số đạt cực tiểu tại điểm 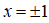 ; giá trị cực tiểu của hàm số là
; giá trị cực tiểu của hàm số là 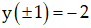
o Đồ thị : Cho 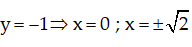
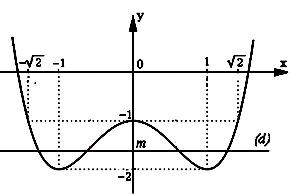
b . Biện luận theo m số nghiệm thực của phương trình: x4 – 2x2 – 1= m
Số nghiệm của (*) là số giao điểm của (C) và đường thẳng d: y= m.
Dựa vào đồ thị, ta thấy :
+ Khi m < -2 thì (*) vô nghiệm.
+ Khi 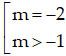 thì (*) có 2 nghiệm.
thì (*) có 2 nghiệm.
+ Khi -2 < m < -1 thì (*) có 4 nghiệm.
+ Khi m = -1 thì (*) có 3 nghiệm
2. Bài luyện tập thêm
1. y = 2x2 – x4
2. y = – x4 + 4x2 – 1
3. y = (x2 –1)(x2+2)
4. y = -x4 + 2x2 + 3
5. y= x4 + 4x2 – 3
6. y=12x4−3x2+32y=12×4−3×2+32

Vậy là các bạn vừa được tìm hiểu các bước khảo sát và vẽ đồ thị hàm số bậc 4 trùng phương . Hi vọng, sau khi chia sẻ cùng bài viết, bạn nắm chắc hơn kiến thức này. Cách khảo sát và vẽ đồ thị hàm số bậc ba Trường Trung Cấp Nghề Thương Mại Du Lịch Thanh Hoá cũng đã chia sẻ rất chi tiết. Bạn tham khảo thêm nhé !
Bản quyền bài viết thuộc Trường Trung Cấp Nghề Thương Mại Du Lịch Thanh Hoá. Mọi hành vi sao chép đều là gian lận!
Nguồn chia sẻ: https://tmdl.edu.vn/huong-dan-cac-buoc-khao-sat-va-ve-do-thi-ham-so-bac-4-trung-phuong/
Hướng dẫn các bước khảo sát và vẽ đồ thị hàm số bậc 4 trùng phương
Ở bài viết trước, Trường Trung Cấp Nghề Thương Mại Du Lịch Thanh Hoá đã giới thiệu đến thầy cô cùng các bạn học sinh các bước khảo sát và vẽ đồ thị hàm số bậc ba. Tiếp nối mạch kiến thức đó, hôm nay chúng tôi sẽ hướng dẫn các bước khảo sát và vẽ đồ thị hàm số bậc 4 trùng phương. Chia sẻ để nắm chắc hơn chuyên đề Đại số quan trọng này nhé !
I. LÝ THUYẾT CHUNG
Bạn đang xem bài: Hướng dẫn các bước khảo sát và vẽ đồ thị hàm số bậc 4 trùng phương
1. Cực trị của hàm bậc 4 là gì?
Cho hàm số bậc 4 : y=f(x)=ax4+bx3+cx2+dx+e với a≠0
Đạo hàm y′=4ax3+3bx2+2cx+d
Hàm số y=f(x) có thể có một hoặc ba cực trị .
Điểm cực trị là điểm mà qua đó thì đạo hàm y′ đổi dấu
2. Số điểm cực trị của hàm bậc 4
Xét đạo hàm y′=4ax3+3bx2+3cx+d
- Nếu y′=0 có đúng 1 nghiệm thì hàm số y=f(x) có đúng 1 cực trị (có thể là cực đại hoặc cực tiểu).
- Nếu y′=0 có 2 nghiệm (gồm 1 nghiệm đơn , 1 nghiệm kép) thì hàm số y=f(x) có đúng 1 cực trị (có thể là cực đại hoặc cực tiểu).
- Nếu y′=0 có 3 nghiệm phân biệt thì hàm số y=f(x) có 3 cực trị (gồm cả cực đại và cực tiểu).
3. Hàm số trùng phương là gì ?
Hàm số trùng phương là hàm số bậc 4 có dạng:
y=f(x)=ax4+bx2+c
Như vậy có thể coi đây là một hàm số bậc 2 với ẩn là x2
4. Điều kiện cực trị của hàm bậc 4 trùng phương


II. CÁC BƯỚC KHẢO SÁT VÀ VẼ ĐỒ THỊ HÀM SỐ BẬC 4 TRÙNG PHƯƠNG
1. Cách khảo sát và vẽ đồ thị hàm số bậc 4 trùng phương
Để khảo sát và vẽ đồ thị hàm số bậc 4 trùng phương ta thực hiện các bước sau đây:
Bước 1: Tìm tập xác định. D=R
Bước 2: Xét sự biến thiên
- Xét chiều biến thiên của hàm số
+ Tính đạo hàm y’ = 4ax3 + 2bx
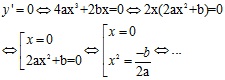
+ Xét dấu đạo hàm y’ và suy ra chiều biến thiên của hàm số.
- Tìm cực trị
- Tìm các giới hạn tại vô cực ( x →± ∞). (Hàm trùng phương không có TCĐ và TCN.)
- Lập bảng biến thiên
Thể hiện đầy đủ và chính xác các giá trị trên bảng biến thiên
Bước 3: Vẽ đồ thị
– Giao của đồ thị với trục Oy: x=0 =>y= c => (0;c)
– Giao của đồ thị với trục Ox:
– Các điểm CĐ; CT nếu có.
(Chú ý: giải phương trình trùng phương- các bạn bấm máy tính như giải pt bậc 2 nhưng chỉ lấy nghiệm không âm, sau đó giải để tìm ra x)
– Lấy thêm một số điểm (nếu cần)- (điều này làm sau khi hình dung hình dạng của đồ thị. Thiếu bên nào học sinh lấy điểm phía bên đó, không lấy tùy tiện mất thời gian.)
– Nhận xét về đặc trưng của đồ thị. Ta có: Nên đồ thị hàm số đã cho là hàm số chẵn. Đồ thị của nó nhận Oy làm trục đối xứng..
2. Các trường hợp biến thiên của đồ thị hàm số bậc 4
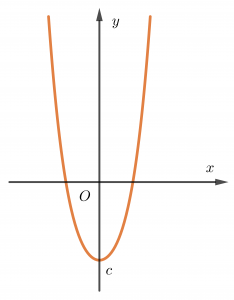
Trường hợp 1. a>0, b≥0
Hàm số đồng biến trên khoảng (0;+∞) và nghịch biến trên (−∞;0).
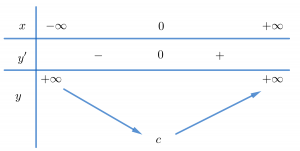
Trường hợp này đồ thị hàm trùng phương có dạng gần giống đồ thị hàm số bậc 2.
Trường hợp 2. a<0, b≤0
Hàm số nghịch biến trên khoảng (0;+∞) và đồng biến trên (−∞;0).
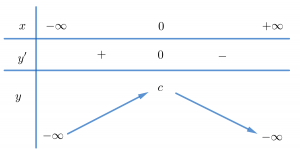
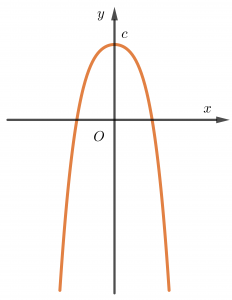
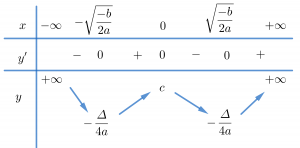
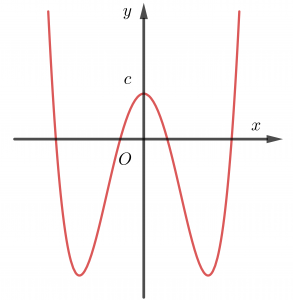
Trường hợp 3. a>0, b<0
Chúng ta thường nhớ hình dáng bảng biến thiên trường hợp này giống chữ W.
Trường hợp 4. a<0, b>0
Chúng ta thường nhớ hình dáng bảng biến thiên trường hợp này giống chữ M.
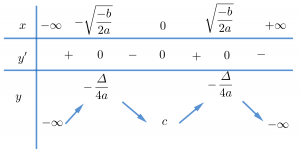
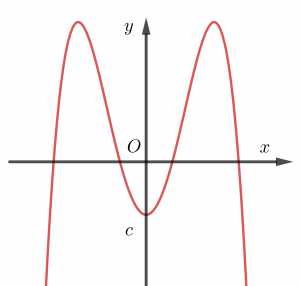
3. Các dạng đồ thị hàm số bậc 4 trùng phương: y = ax4 + bx2 + c (a≠0)

III. BÀI TẬP VỀ ĐỒ THỊ HÀM SỐ BẬC 4 TRÙNG PHƯƠNG
1. Bài tập có lời giải
Bài 1:
Cho hàm số y = x4 – 2x2 – 1 có đồ thị (C).
a. Khảo sát sự biến thiên và vẽ đồ thị (C) của hàm số;
b. Dùng đồ thị (C), hãy biện luận theo m số nghiệm thực của phương trình x4 – 2x2 – 1= m (*)
a. Khảo sát sự biến thiên và vẽ đồ thị:
* Tập xác định: D= R.
* Chiều biến thiên :
Ta có : y’= 4x3 – 4x = 4x (x2 -1)
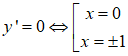
Giới hạn của hàm số tại vô cực: 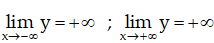
o Bảng biến thiên :
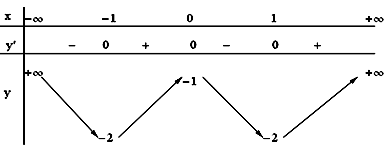
Hàm số nghịch biến trên các khoảng 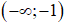 và (0; 1), đồng biến trên các khoảng (-1; 0) và
và (0; 1), đồng biến trên các khoảng (-1; 0) và 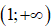
Hàm số đạt cực đại tại điểm x= 0 ; giá trị cực đại của hàm số là y(0) = – 1.
Hàm số đạt cực tiểu tại điểm 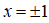 ; giá trị cực tiểu của hàm số là
; giá trị cực tiểu của hàm số là 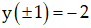
o Đồ thị : Cho 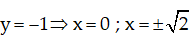
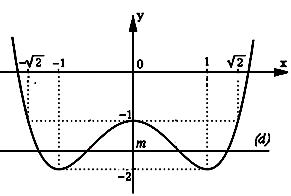
b . Biện luận theo m số nghiệm thực của phương trình: x4 – 2x2 – 1= m
Số nghiệm của (*) là số giao điểm của (C) và đường thẳng d: y= m.
Dựa vào đồ thị, ta thấy :
+ Khi m < -2 thì (*) vô nghiệm.
+ Khi 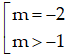 thì (*) có 2 nghiệm.
thì (*) có 2 nghiệm.
+ Khi -2 < m < -1 thì (*) có 4 nghiệm.
+ Khi m = -1 thì (*) có 3 nghiệm
2. Bài luyện tập thêm
1. y = 2x2 – x4
2. y = – x4 + 4x2 – 1
3. y = (x2 –1)(x2+2)
4. y = -x4 + 2x2 + 3
5. y= x4 + 4x2 – 3
6. y=12x4−3x2+32y=12×4−3×2+32

Vậy là các bạn vừa được tìm hiểu các bước khảo sát và vẽ đồ thị hàm số bậc 4 trùng phương . Hi vọng, sau khi chia sẻ cùng bài viết, bạn nắm chắc hơn kiến thức này. Cách khảo sát và vẽ đồ thị hàm số bậc ba Trường Trung Cấp Nghề Thương Mại Du Lịch Thanh Hoá cũng đã chia sẻ rất chi tiết. Bạn tham khảo thêm nhé !
Bản quyền bài viết thuộc Trường Trung Cấp Nghề Thương Mại Du Lịch Thanh Hoá. Mọi hành vi sao chép đều là gian lận!
Nguồn chia sẻ: https://tmdl.edu.vn/huong-dan-cac-buoc-khao-sat-va-ve-do-thi-ham-so-bac-4-trung-phuong/
Trang chủ: tmdl.edu.vn
Danh mục bài: Giáo dục