Lý thuyết phép đối xứng trục và phương pháp giải các dạng toán thường gặp
Phép đối xứng trục là một trong những phần kiến thức trọng tâm của chương trình Hình học 11. Bài viết hôm nay, Trường Trung Cấp Nghề Thương Mại Du Lịch Thanh Hoá sẽ giới thiệu chi tiết về chuyên đề này: từ phần lý thuyết đến phương pháp giải các dạng toán thường gặp của phép đối xứng trục. Các bạn chia sẻ nhé !
I. LÝ THUYẾT VỀ PHÉP ĐỐI XỨNG TRỤC
Bạn đang xem bài: Lý thuyết phép đối xứng trục và phương pháp giải các dạng toán thường gặp
1. Định nghĩa
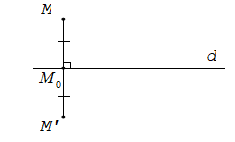
Cho đường thẳng d. Phép biến hình biến mỗi điểm M thuộc d thành chính nó, biến mỗi điểm M không thuộc d thành M’ sao cho d là đường trung trực của đoạn thẳng MM’ được gọi là phép đối xứng qua đường thẳng d hay phép đối xứng trục d.
Đường thẳng d được gọi là trục của phép đối xứng hoặc đơn giản gọi là trục đối xứng.
Phép đối xứng trục d thường được kí hiệu là Đd
Nếu hình H’ là ảnh của hình H qua phép đối xứng trục d thì ta còn nói H đối xứng với H’ qua d, hay H và H’ đối xứng với nhau qua d.
Nhận xét
Cho đường thẳng d. Với mỗi điểm M gọi M0 là hình chiếu vuông góc của M trên đường thẳng d. Khi đó M’ = Đd(M) ⇔ M0M’→ = – M0M→.
M’ = Đd(M) ⇔ M = Đd(M’)
2. Biểu thức toạ độ
Nếu d ≡ Ox. Gọi M’(x’; y’) = ĐOx[M(x,y)] thì
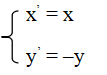
Nếu d ≡ Oy. Gọi M’(x’; y’) = ĐOy[M(x,y)] thì
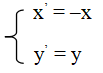
3. Tính chất
Tính chất 1
Phép đối xứng trục bảo toàn khoảng cách giữa hai điểm bất kì.
Tính chất 2
Phép đối xứng trục biến đường thẳng thành đường thẳng, biến đoạn thẳng thành đoạn thẳng bằng nó, biến tam giác thành tam giác bằng nó, biến đường tròn thành đường tròn có cùng bán kính.
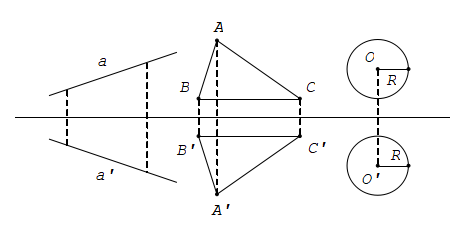
4. Trục đối xứng của một hình
Định nghĩa
Đường thẳng d gọi là trục đối xứng của hình H nếu phép đối xứng qua d biến hình H thành chính nó. Khi đó ta nói H là hình có trục đối xứng.
II.PHƯƠNG PHÁP GIẢI CÁC DẠNG TOÁN CỦA PHÉP ĐỐI XỨNG TRỤC
Dạng 1: Dùng phép đối xứng trục để giải các bài toán dựng hình
Phương pháp giải:
– Dựng điểm M: Tìm một hình (H) cố định và đường thẳng d cố định cho trước sao cho khi thực hiện phép đối xứng trục d ta có được ảnh là hình (H’) giao với (C) cố định tại điểm M cần dựng
– Thực hiện các phép đối xứng trục d để tìm các điểm còn lại từ đó ta có hình cần dựng
Ví dụ 1: Dựng hình vuông ABCD biết hai đỉnh A và C nằm trên đường thẳng d1 và hai đỉnh B, D lần lượt thuộc hai đường thẳng d2,d3
Lời giải
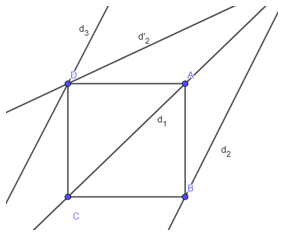
– Giả sử đã dựng được hình vuông ABCD thỏa điều kiện của bài toán
Do và AC là trục đối xứng của hình vuông ABCD
Mặt khác B ∈ d2 nên D ∈ d‘2 trong đó d‘2 là đường thẳng đối xứng với d2 qua
Suy ra: D = d‘2 ∩ d3
– Cách dựng:
Dựng d‘2 = Dd1(d2), gọi D = d3 ∩ d‘2
Dựng đường thẳng qua D vuông góc với d1 tại O và cắt d2 tại B
Dựng đường tròn tâm O đường kính BD cắt tại A, C (A, C theo thứ tự để tạo thành tứ giác ABCD)
– Nhận xét:
TH1: d2 cắt d3 khi đó:
Nếu d‘2 ∩ d3 thì bài toán có 1 nghiệm hình
Nếu d‘2 // d3 thì bài toán có vô nghiệm hình
TH2: d2 // d3. Khi đó
Nếu d1 song song và cách đều d2 và d3 thì bài toán có vô số nghiệm hình
Nếu d1 hợp với d2 và d3 một góc 45 thì bài toán có 1 nghiệm hình
Nếu d1 song song và không cách đều d2, d3 hoặc d1 không hợp với d2, d3 một góc 45 thì bài toán vô nghiệm hình
Ví dụ 2: Cho hai đường tròn (C), (C′) có bán kính khác nhau và đường thẳng d. Hãy dựng hình vuông ABCD có hai đỉnh A, C lần lượt nằm trên (C), (C′) và hai đỉnh còn lại nằm trên d
Lời giải
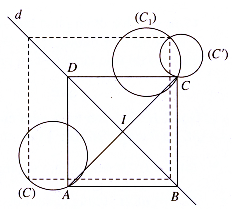
– Dựng đường tròn (C1) là ảnh của (C) qua Dd
– Gọi C là giao điểm của (C1) và (C’)
– Dựng điểm A đối xứng với C qua d
– Gọi I = AC ∩ d
Lấy trên d hai điểm B, D sao cho: IB = ID = IA
Khi đó ABCD là hình vuông cần dựng
Số nghiệm hình bằng số giao điểm của (C1) và (C’)
Dạng 2: Xác định ảnh của một hình qua phép đối xứng trục
Phương pháp giải: Để xác định ảnh (H′) của hình (H) qua phép đối xứng trục ta có thể dùng một trong các cách sau:
– Dùng định nghĩa phép đối xứng trục
– Dùng biểu thức tọa độ của phép đối xứng trục mà trục đối xứng là các trục tọa độ Ox, Oy
– Dùng biểu thức vectơ của phép đối xứng trục
Ví dụ 1: Trong mặt phẳng Oxy cho A (1; -2) và B (3; 1). Tìm ảnh của A, B và đường thẳng AB qua phép đối xứng trục Ox
Lời giải
A’ là ảnh của A qua phép đối xứng qua trục Ox có tọa độ là A’ (1; 2)
B’ là ảnh của B qua phép đối xứng qua trục Ox có tọa độ là B’ (3; -1)
Ảnh của đường thẳng AB qua phép đối xứng qua trục Ox chính là đường thẳng A’B’ nên đường thẳng A’B’ có phương trình:
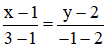
=> 3x + 2y – 7 = 0
Ví dụ 2: Trong mặt phẳng Oxy có đường thẳng d có phương trình: 3x – y + 2 = 0. Viết phương trình đường thẳng d’ là ảnh của đường thẳng d qua phép đối xứng trục Oy
Lời giải
Gọi M (x; y) tùy ý thuộc d
Suy ra: 3x – y + 2 = 0 (1)
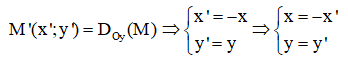
Thay vào (1) được: 3(-x‘) – y‘ + 2 = 0 ⇔ 3x‘ + y‘ – 2 = 0
Vậy tọa độ M’ thỏa mãn phương trình d’: 3x + y – 2 = 0
Dạng 3: Dùng phép đối xứng trục để giải các bài tập hợp điểm
Phương pháp giải:
– Tìm quỹ tích điểm M: Từ giả thiết chọn điểm E di động sao cho EM nhận đường thẳng d cố định làm trục đối xứng
– Xác định hình (H) là quỹ tích của E
– Khi đó tập hợp các điểm M là (H’) – ảnh của (H) qua phép đối xứng trục d
Ví dụ 1: Cho A, B, C thuộc đường thẳng xx’ (B nằm giữa A và C). Một đường thẳng yy‘ ⊥ xx‘ tại C. Qua điểm A dựng đường thẳng di động Δ cắt yy’ tại M. Qua B dựng đường vuông góc với Δ cắt yy’ tại N. Chứng minh khi Δ quay quanh A thì đường tròn ngoại tiếp tam giác BMN còn đi qua một điểm cố định thứ hai
Lời giải
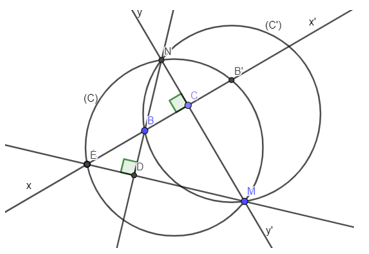
Gọi (C) là đường tròn ngoại tiếp tam giác AMN:
BN ⊥ AM
AC ⊥ MN
Nên suy ra B là trực tâm của tam giác AMN
Gọi B’ là giao điểm của xx’ và đường tròn (C)
Dễ chứng minh được yy’ là trục đối xứng của BB’
Do đó B thuộc đường tròn (C‘) = Dyy’ [(C)]
Vậy B‘ ∈ (C) = Dyy’ [(C‘)]
Ví dụ 2: Cho tam giác ABC có hai đỉnh B, C di động trên đường thẳng cố định Δ Biết rằng trực tâm H của tam giác cố định và đường tròn ngoại tiếp tam giác ABC luôn đi qua một điểm cố định P khác H. Gọi O là tâm đường tròn ngoại tiếp tam giác ABC. Tìm quỹ tích điểm O
Lời giải
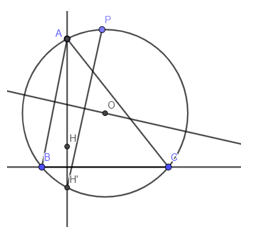
Gọi H‘ = DΔ(H)
Suy ra H’ cố định và thuộc đường tròn (O)
Do đó O cách đều hai điểm cố định P và H’
Suy ra O thuộc đường trung trực PH’
III. BÀI TẬP VẬN DỤNG
Bài 1: Cho hai đường thẳng a và b cắt nhau tại O. Xét 2 phép đối xứng trục Đa và Đb:
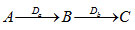
Khẳng định nào sau đây không sai?
A. A, B, C đường tròn (O, R =OC)
B. Tứ giác OABC nội tiếp
C. DABC cân ở B
D. DABC vuông ở B.
Đáp án: A
Bài 2. Gọi d là phân giác trong tại A của DABC, B’ là ảnh của B qua phép đối xứng trục Đd. Khẳng định nào sau đây sai?
A. Nếu AB < AC thì B’ thì B’ ở trên cạnh AC
B. B’ là trung điểm cạnh AC
C. Nếu AB = AC thì B ≡ C
D. Nếu B’ là trung điểm cạnh AC thì AC = 2AB
Đáp án: B
Bài 3. Trong mặt phẳng Oxy cho điểm M(-3; 2), đường thẳng (D): x + 3y – 8 = 0, đường tròn (C ): (x + 3)2 + (y + 2)2 = 4. Tìm ảnh của M, (D) và (C) qua phép đối xứng trục (a): x – 2y + 2 = 0
Đáp án:
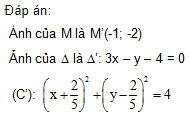
Bài 4. Trong mặt phẳng Oxy cho điểm M(3; -5), đường thẳng (D): 3x + 2y – 6 = 0, đường tròn (C ): (x + 1)2 + (y -2)2 = 9. Tìm ảnh của M, (D) và (C) qua phép đối xứng trục (a): 2x – y + 1 = 0
Đáp án
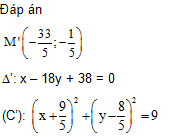
Bài 5. Trong mặt phẳng Oxy cho đường thẳng (a): 2x – y – 3 = 0, (D): x – 3y + 11 = 0, (C) x2 + y2 – 10x – 4y + 27 = 0
a . Viết biểu thức giải thích của phép đối xứng trục Đa.
b. Tìm ảnh của điểm M(4; -1) qua Đa.
c. Tìm ảnh: (D’) = Đa(D), (C’) = Đa(C).
Đáp án:
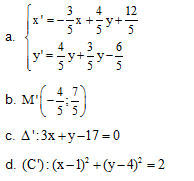
Bài 6. Cho hai điểm phân biệt B và C cố định trên đường tròn (O), điểm A di động trên đường tròn (O). Chứng minh rằng khi A di động trên đường tròn (O) thì trực tâm của tam giác ABC di động trên một đường tròn.
Trên đây, chúng tôi đã giới thiệu đến quý thầy cô và các bạn Lý thuyết phép đối xứng trục và phương pháp giải các dạng toán thường gặp của phép đối xứng trục. Hi vọng, chúng tôi đã cung cấp thêm cho bạn nguồn tư liệu thiết yếu, giúp các bạn dạy và học tốt hơn. Xem thêm phép đối xứng tâm bạn nhé !
Bản quyền bài viết thuộc Trường Trung Cấp Nghề Thương Mại Du Lịch Thanh Hoá. Mọi hành vi sao chép đều là gian lận!
Nguồn chia sẻ: https://tmdl.edu.vn https://tmdl.edu.vn/ly-thuyet-phep-doi-xung-truc-va-phuong-phap-giai-cac-dang-toan-thuong-gap/
Trang chủ: tmdl.edu.vn
Danh mục bài: Giáo dục