N là tập hợp số gì? N là gì trong toán học?

Mời các em cùng Trường Trung Cấp Nghề Thương Mại Du Lịch Thanh Hoá tìm hiểu N là tập hợp số gì? N là gì trong toán học? trong bài viết dưới đây.

N là tập hợp số gì?

Trong toán học, N là ký hiệu của tập số tự nhiên. Các số 0; 1; 2; 3; … là các số tự nhiên. Người ta kí hiệu tập hợp các số tự nhiên là N.

Bạn đang xem bài: N là tập hợp số gì? N là gì trong toán học?

Chúng ta có số tự nhiên nhỏ nhất là số 0. Không tồn tại số tự nhiên lớn nhất.

Ta có 2 kí hiệu tập hợp là N và N*.

=> Nắm rõ hơn về số tự nhiên là gì?

– Tập hợp N

N là ký hiệu của tập hợp các số tự nhiên lớn hơn hoặc bằng 0.

N = {0;1;2;3; …}.

– Tập hợp N*

Còn N* là tập hợp các số tự nhiên lớn hơn 0.

N* = {1;2;3;…}.

– Biểu diễn tia

Hình vẽ dưới đây biểu diễn dãy số tự nhiên theo hình tia.

Tập hợp số tự nhiên

– Các số tự nhiên được biểu diễn trên tia số bởi các điểm cách đều nhau như hình dưới đây

– Mỗi số tự nhiên được biểu diễn bằng một điểm trên tia số; điểm biểu diễn số tự nhiên n gọi là điểm n

– Nếu số a nhỏ hơn số b ta viết a < b (a nhỏ hơn b). Ta cũng nói số b lớn hơn số a và viết b > a.

– Khi biểu diễn trên tia số nằm ngang có chiều mũi tên đi trái sang phải, nếu a < b thì điểm a nằm bên trái điểm b.

Ta viết a ≤ b để chỉ a < b hoặc a = b, b ≥ a để chỉ b > a hoặc a = b.

Mỗi số tự nhiên có một số liền sau cách nó một đơn vị.

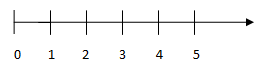
– Tính chất bắc cầu: Nếu a < b và b < c thì a < c

Những tính chất của số tự nhiên

– Dãy số tự nhiên liên tiếp sẽ có tính tăng dần, hai số liên tiếp sẽ có một số nhỏ và một số lớn hơn.

– Mỗi số tự nhiên chỉ có một số liền sau duy nhất. Ví dụ số liền sau của 3 là số 4.

– Khi số a nhỏ hơn số b, ta viết a < b=”” hoặc=”” b=””> a. Nếu a < b,=”” b=””>< c=”” thì=”” ta=”” có=”” a=””><>

– Trong hình tia, chiều mũi tên sẽ đi từ trái sang phải. Các điểm trên tia phải có tính tăng dần.

– Mỗi số tự nhiên có một số liền trước duy nhất, trừ số 0 vì số 0 là bé nhất.

– Số 0 là số tự nhiên bé nhất, không tồn tai số lớn nhất.

– Tổng số phần tử của tập hợp các số tự nhiên là vô số.

Thứ tự trong dãy số tự nhiên

Trong dãy số tự nhiên:

+ Cộng thêm 1 đơn vị vào bất cứ số nào cũng được số tự nhiên liền sau số đó. Vì vậy, không có số tự nhiên lớn nhất và dãy số tự nhiên có thể kéo dài mãi.

Ví dụ 1:

+ Khi cộng thêm 1 đơn vị vào số 1 000 000 được số tự nhiên liền sau là 1 000 001

+ Khi cộng thêm 1 đơn vị vào số 1 000 001 được số tự nhiên liền sau là 1000002, …

+ Bớt đi 1 đơn vị vào bất kì số nào (khác số 0) cũng được số tự nhiên liền trước số đó.

Ví dụ 2:

+ Bớt đi 1 đơn vị ở số 1 được số tự nhiên liền trước là số 0.

* Chú ý: Không có số tự nhiên nào liền trước số 0 nên số 0 là số tự nhiên bé nhất.

Trong dãy số tự nhiên, hai số liên tiếp thì hơn hoặc kém nhau 1 đơn vị.

Ví dụ 3: Tìm số liền trước, liền sau của các số dưới đây:

Lời giải:

Số liền trước của 56 là 55. Số liền sau của 56 là 57.

Số liền trước của 372 là 371. Số liền sau của 372 là 373.

Số liền trước của 5729 là 5728. Số liền sau của 5729 là 5730.

Số liền trước của 466 là 465. Số liền sau của 466 là 467.

Ví dụ 4: Điền số thích hợp vào chỗ chấm:

Lời giải:

Trong dãy số 162, …., 164, ta cần điền thêm số 163 để được ba số tự nhiên liên tiếp.

Trong dãy số …., 472, 473, ta cần điền thêm số 471 để được ba số tự nhiên liên tiếp.

Trong dãy số 856, 857, …., ta cần điền thêm số 858 để được ba số tự nhiên liên tiếp.

Các phép toán trên tập hợp số tự nhiên

– Phép cộng

1. a + 0 = a.

2. a + S(b) = S(a) + b.

Nếu chúng ta ký hiệu S(0) là 1, khi đó S(b) = S(b + 0) = b + 1. Tức là, số liền sau của b chẳng qua là b + 1.

– Phép nhân

Tương tự như phép cộng, chúng ta định nghĩa phép nhân như sau:

1. a × 0 = 0.

2. a × S(b) = (a × b) + a.Phép cộng và phép nhân thỏa tính chất phân phối: a × (b + c) = (a × b) + (a × c).

Nếu chúng ta hiểu tập hợp số tự nhiên theo nghĩa “không có số 0” và “bắt đầu bằng số 1” thì các định nghĩa về phép + và × cũng vẫn thế, ngoại trừ sửa lại a + 1 = S(a) và a × 1 = a.

Trong phần còn lại của bài này, chúng ta viết a.b để ám chỉ tích a × b, và chúng ta cũng sẽ thừa nhận quy định về thứ tự thực hiện các phép toán.

– Phép chia có dư và tính chia hết

Cho hai số tự nhiên a,b, ngoài ra b ≠ 0. Xét tập hơp M các số tự nhiên p sao cho p.b ≤ a. Tập này bị chặn nên có một phần tử lớn nhất, gọi phần tử lớn nhất của M là q. Khi đó bq ≤ a và b(q+1) > a. Đặt r = a – b.q. Khi đó ta có a = b.q + r, trong đó 0 ≤ r <>

Số q được gọi là thương, số r được gọi là số dư khi chia a cho b. Nếu r = 0 thì a = b.q. Khi đó ta nói rằng a chia hết cho b hay b chia hết a. Khi đó ta cũng nói rằng b là ước của a, a là bội của b.

Những bài tập cơ bản về số tự nhiên

Có thể những thông tin bên trên khá lý thuyết với các bạn học sinh thì sau đây với những bài tập ví dụ về cộng trừ nhân chia sẻ giúp các bạn học sinh phần nào hình dung ra về bài tập số tự nhiên là như thế nào nhé:

Bài tập số tự nhiên Phép cộng:

1. a + 0 = a.
2. a + S(b) = S(a) + b.

Nếu chúng ta ký hiệu S(0) là 1, khi đó S(b) = S(b + 0) = b + 1. Tức là, số liền sau của b chẳng qua là b + 1.

Ví dụ: Đề bài: Tính giá trị của A biết: A = 1 + 2 + 3 + 4 + …. + 2014.

Phân tích: Đây là dạng bài cơ bản trong dạng bài tính tổng của dãy có quy luật cách đều, cần tính giá trị của A theo công thức tính tổng của dãy số cách đều.

Bài giải

Dãy số trên có số số hạng là: (2014 – 1) : 1 + 1 = 2014 (số hạng)

Giá trị của A là: (2014 + 1) x 2014 : 2 = 2029105

Đáp số: 2029105

Bài tập số tự nhiên Phép nhân:

Tương tự như phép cộng, chúng ta định nghĩa phép nhân như sau:

1. a × 0 = 0.
2. a × S(b) = (a × b) + a.Phép cộng và phép nhân thỏa tính chất phân phối: a × (b + c) = (a × b) + (a × c).

Nếu chúng ta hiểu tập hợp số tự nhiên theo nghĩa “không có số 0” và “bắt đầu bằng số 1” thì các định nghĩa về phép + và × cũng vẫn thế, ngoại trừ sửa lại a + 1 = S(a) và a × 1 = a.

Trong phần còn lại của bài này, chúng ta viết a.b để ám chỉ tích a × b, và chúng ta cũng sẽ thừa nhận quy định về thứ tự thực hiện các phép toán.

Ví dụ: Đề bài: Cho T = 2 x 2 x 2 x … x 2 x 2 (tích có 2013 thừa số 2). T có chữ số tận cùng là mấy?

Giải:

Cho T = 2 x 2 x 2 x … x 2 x 2 (tích có 2013 thừa số 2).

Tích có các thừa số đều là 2 có tính chất sau:

Cứ 4 thừa số 2 có tích tận cùng lần lượt là 2; 4; 8 và 6

Mà 2013 : 4 = 503 (nhóm) dư 1.

Cuối mỗi nhóm tích tận cùng là 6 và đầu mỗi nhóm là chữ số 2. Vậy T có số nhóm dư 1 thì chữ số tận cùng của T là 2

Bài tập số tự nhiên Phép chia (có dư và chia hết):

Cho hai số tự nhiên a,b, ngoài ra b ≠ 0. Xét tập hơp M các số tự nhiên p sao cho p.b ≤ a. Tập này bị chặn nên có một phần tử lớn nhất, gọi phần tử lớn nhất của M là q. Khi đó bq ≤ a và b(q+1) > a. Đặt r = a – b.q. Khi đó ta có a = b.q + r, trong đó 0 ≤ r <>

Số q được gọi là thương, số r được gọi là số dư khi chia a cho b. Nếu r = 0 thì a = b.q. Khi đó ta nói rằng a chia hết cho b hay b chia hết a. Khi đó ta cũng nói rằng b là ước của a, a là bội của b.

Ví dụ: Đề bài: Có bao nhiêu số có 3 chữ số khác nhau chia hết cho 5

Giải

Số chia hết cho 5 thì có tận cùng bằng 0 hoặc bằng 5.

Tận cùng bằng 0:

Có 1 cách chọn chữ số hàng đơn vị (là 0)

Có 9 cách chọn chữ số hàng trăm.

Có 8 cách chọn chữ số ngành chục.

Vậy có: 1 x 9 x 8 = 72 (số)

Hi vọng với bài viết về N là tập hợp số gì? N là gì trong toán học? các em đã phần nào hiểu hơn về số tự nhiên rồi nhé.

Bản quyền bài viết thuộc Trường Trung Cấp Nghề Thương Mại Du Lịch Thanh Hoá. Mọi hành vi sao chép đều là gian lận!
Nguồn chia sẻ: https://tmdl.edu.vn https://tmdl.edu.vn/n-la-tap-hop-so-gi/

Trang chủ: tmdl.edu.vn
Danh mục bài: Giáo dục