Phương trình chứa dấu Giá trị tuyệt đối và cách giải – Toán lớp 8

Phương trình chứa dấu giá trị tuyệt đối ở lớp 8 dù không được nhắc tới nhiều và thời gian dành cho nội dung này cũng khá ít. Vì vậy, dù đã làm quen một số dạng toán về giá trị tuyệt đối ở các lớp trước nhưng rất nhiều em vẫn mắc sai sót khi giải các bài toán này.

Trong bài viết này, chúng ta cùng ôn lại cách giải một số dạng phương trình chứa dấu giá trị tuyệt đối. Qua đó vận dụng làm bài tập để rèn luyện kỹ năng giải phương trình có chứa dấu giá trị tuyệt đối.

Bạn đang xem bài: Phương trình chứa dấu Giá trị tuyệt đối và cách giải – Toán lớp 8

I. Kiến thức cần nhớ

1. Giá trị tuyệt đối

• Với a ∈ R, ta có: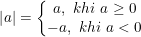 

2. Dấu của nhị thức bậc nhất

a) Định nghĩa:

– Nhị thức bậc nhất của x là biểu thức có dạng f(x) = ax + b, trong đó a,b là các số cho trước và a ≠ 0.

– Số x₀ = -b/a thỏa mãn f(x₀) = 0 gọi là nghiệm của nhị thức bậc nhất f(x).

b) Quy tắc dấu:

– Nhị thức bậc nhất f(x) = ax + b cùng dấu với a khi x > x₀; và trái dấu với a khi x < x₀; cụ thể:

¤ Nếu a > 0 thì f(x) > 0, ∀x > x₀ và f(x) < 0,  ∀x < x₀ như bảng sau:

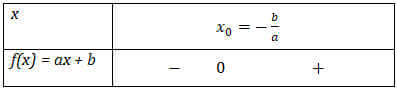
¤ Nếu a < 0 thì f(x) < 0, ∀x > x₀ và f(x) > 0,  ∀x < x₀ như bảng sau:

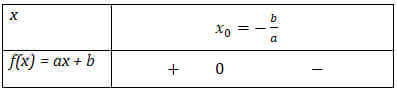
* Cách nhớ: Để ý bên phải nghiệm x₀ thì f(x) cùng dấu với a, bên trái nghiệm x₀ thì f(x) khác dấu với a, nên cách nhớ là: “Phải cùng, Trái khác”

II. Các dạng toán phương trình chứa dấu giá trị tuyệt đối.

° Dạng 1: Phương trình chứa dấu giá trị tuyệt đối dạng |P(x)| = k

* Phương pháp giải:

• Để giải phương trình chứa dấu giá trị tuyệt đối dạng |P(x)| = k, (trong đó P(x) là biểu thức chứa x, k là 1 số cho trước) ta làm như sau:

– Nếu k < 0 thì không có giá trị nào của x thỏa mãn đẳng thức (trị tuyệt đối của mọi số đều không âm).

– Nếu k = 0 thì ta có |P(x)| = 0 ⇔ P(x) = 0

– Nếu k > 0 thì ta có: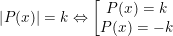 

* Ví dụ: Giải phương trình sau:

a)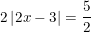     b)

° Lời giải:

a)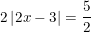

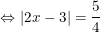
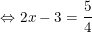  hoặc 

•TH1:  

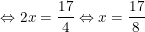
•TH2:  

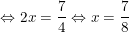
– Kết luận: Vậy phương trình có 2 nghiệm x = 17/8 và x = 7/8.

b) 

 hoặc 

• TH1: 

• TH2: 

– Kết luận: Có 2 giá trị của x thỏa điều kiện là x = 1 hoặc x = 3/4.

* Ví dụ 2: Giải và biện luận theo m phương trình |2 – 3x| = 2m – 6. (*)

° Lời giải:

– Nếu 2m – 6 < 0 ⇒ m < 3 thì pt (*) vô nghiệm

– Nếu 2m – 6 = 0 ⇒ m = 3 thì pt (*) trở thành

|2 – 3x| = 0 ⇔ 2 – 3x = 0 ⇔ x = 2/3. (Phương trình có nghiệm duy nhất).

– Nếu 2m – 6 > 0  ⇒ m > 3 thì pt (*)

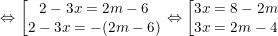
(Phương trình có 2 nghiệm)

• Kết luận: m = 0 pt(*) vô nghiệm

m = 3 pt(*) có nghiệm duy nhất x =2/3

m > 3 pt(*) có 2 nghiệm x = (8-2m)/3 và x = (2m-4)/3.

° Dạng 2: Phương trình chứa dấu giá trị tuyệt đối dạng |P(x)| = |Q(x)|

* Phương pháp giải:

• Để tìm x trong bài toán dạng dạng |P(x)| = |Q(x)|, (trong đó P(x) và Q(x)là biểu thức chứa x) ta vận dụng tính chất sau:

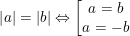 tức là: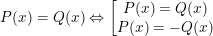 

* Ví dụ: Tìm x biết:

a)|5x – 4| = |x + 4|

b)|7x – 1| – |5x + 1| = 0

* Lời giải:

a)|5x – 4| = |x + 4|

– Vậy x = 2 và x = 0 thỏa điều kiện bài toán

b)|7x – 1| – |5x + 1| = 0 ⇔ |7x – 1| = |5x + 1|

– Vậy x = 1 và x = 0 thỏa điều kiện bài toán.

° Dạng 3: Phương trình chứa dấu giá trị tuyệt đối dạng |P(x)| = Q(x)

* Phương pháp giải:

• Để giải phương trình chứa dấu giá trị tuyệt đối dạng |P(x)| = Q(x) (*), (trong đó P(x) và Q(x)là biểu thức chứa x) ta thực hiện 1 trong 2 cách sau:

* Cách giải 1:

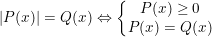 hoặc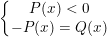 

* Cách giải 2: 

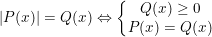 hoặc 

* Ví dụ 1 (Bài 36 trang 51 SGK Toán 8 tập 2): Giải các phương trình:

a) |2x| = x – 6.     b) |-3x| = x – 8

c) |4x| = 2x + 12.     d) |-5x| – 16 = 3x

° Lời giải:

a) |2x| = x – 6 (1)

* Sử dụng cách giải 1:

– Ta có: |2x| = 2x khi x ≥ 0

|2x| = -2x khi x < 0.

– Với x ≥ 0 phương trình (1) ⇔ 2x = x – 6 ⇔ x = -6

Giá trị x = -6 không thỏa mãn điều kiện x ≥ 0 nên không phải nghiệm của (1)

– Với x < 0 phương trình (1) ⇔ -2x = x – 6 ⇔ -3x = -6 ⇔ x = 2.

Giá trị x = 2 không thỏa mãn điều kiện x < 0 nên không phải nghiệm của (1).

+ Kết luận: Vậy phương trình (1) vô nghiệm.

* Sử dụng cách giải 2:

– Ta có: x – 6 ≥ 0 ⇒ x ≥ 6.

 hoặc 

 hoặc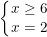 

– Ta thấy x = -6 và x = 2 đều không thỏa điều kiện x ≥ 6 nên pt(1) vô nghiệm.

– Kết luận: Phương trình vô nghiệm

b) |-3x| = x – 8 (2)

– Ta có: |-3x| = -3x khi -3x ≥ 0 ⇔ x ≤ 0.

|-3x| = -(-3x) = 3x khi -3x < 0 ⇔ x > 0.

– Với x ≤ 0 phương trình (2) ⇔ -3x = x – 8 ⇔ -4x = -8 ⇔ x = 2

Giá trị x = 2 không thỏa mãn điều kiện x ≤ 0 nên không phải nghiệm của (2).

– Với x > 0 Phương trình (2) ⇔ 3x = x – 8 ⇔ 2x = -8 ⇔ x = -4.

Giá trị x = -4 không thỏa mãn điều kiện x > 0 nên không phải nghiệm của (2).

– Kết luận: Phương trình (2) vô nghiệm.

c) |4x| = 2x + 12 (3)

– Ta có: |4x| = 4x khi 4x ≥ 0 ⇔ x ≥ 0

|4x| = -4x khi 4x < 0 ⇔ x < 0.

– Với x ≥ 0  phương trình (3) ⇔ 4x = 2x + 12 ⇔ 2x = 12 ⇔ x = 6.

Giá trị x = 6 thỏa mãn điều kiện x ≥ 0 nên là nghiệm của (3)

– Với x < 0 phương trình (3) ⇔ -4x = 2x + 12 ⇔ -6x = 12 ⇔ x = -2.

Giá trị x = -2 thỏa mãn điều kiện x < 0 nên là nghiệm của (3).

– Kết luận: Phương trình có hai nghiệm x = 6 và x = -2.

d) |-5x| – 16 = 3x (4)

– Ta có: |-5x| = -5x khi -5x ≥ 0 ⇔ x ≤ 0.

|-5x| = -(-5x) = 5x khi -5x < 0 ⇔ x > 0.

– Với x ≤ 0 phương trình (4) ⇔ -5x – 16 = 3x ⇔ -5x – 3x = 16 ⇔ -8x = 16 ⇔ x = -2.

Giá trị x = -2 thỏa mãn điều kiện x ≤ 0 nên là nghiệm của (4).

– Với x > 0 phương trình (4) ⇔ 5x – 16 = 3x ⇔ 5x – 3x = 16 ⇔ 2x = 16 ⇔ x = 8

Giá trị x = 8 thỏa mãn điều kiện x > 0 nên là nghiệm của (4).

– Kết luận: Phương trình có hai nghiệm nghiệm x = -2 và x = 8.

* Ví dụ 2 (Bài 37 trang 51 SGK Toán 8 tập 2): Giải các phương trình:

a) |x – 7| = 2x + 3.   b) |x + 4| = 2x – 5

c) |x+ 3| = 3x – 1.     d) |x – 4| + 3x = 5

° Lời giải:

a) |x – 7| = 2x + 3 (1)

– Ta có: |x – 7| = x – 7 khi x – 7 ≥ 0 ⇔ x ≥ 7.

|x – 7| = -(x – 7) = 7 – x khi x – 7 < 0 ⇔ x < 7.

– Với  x ≥ 7 phương trình (1) ⇔ x – 7 = 2x + 3 ⇔ x = -10.

Giá trị x = -10 không thỏa mãn điều kiện x ≥ 7 nên không phải nghiệm của (1).

– Với x < 7 phương trình (1) ⇔ 7 – x = 2x + 3 ⇔ 3x = 4 ⇔ x = 4/3

Giá trị x = 4/3 thỏa mãn điều kiện x < 7 nên là nghiệm của (1)

– Kết luận: Phương trình (1) có một nghiệm x = 4/3.

b) |x + 4| = 2x – 5 (2)

– Ta có: |x + 4| = x + 4 khi x + 4 ≥ 0 ⇔ x ≥ -4.

|x + 4| = -(x + 4) = -x – 4 khi x + 4 < 0 ⇔ x < -4.

– Với x ≥ -4 phương trình (2) ⇔ x + 4 = 2x – 5 ⇔ x = 9

Giá trị x = 9 thỏa mãn điều kiện x ≥ -4 nên là nghiệm của (2).

– Với x < -4 phương trình (2) ⇔ –x – 4 = 2x – 5 ⇔ 3x = 1 ⇔ x = 1/3

Giá trị x = 1/3 không thỏa mãn điều kiện x < -4 nên không phải nghiệm của (2)

– Kết luận: Phương trình có một nghiệm x = 9.

c) |x + 3| = 3x – 1 (3)

– Ta có : |x + 3| = x + 3 khi x + 3 ≥ 0 ⇔ x ≥ -3.

|x + 3| = -(x + 3) = -x – 3 khi x + 3 < 0 ⇔ x < -3.

– Với x ≥ -3 phương trình (3) ⇔ x + 3 = 3x – 1 ⇔ 2x = 4 ⇔ x = 2.

Giá trị x = 2 thỏa mãn điều kiện x ≥ -3 nên là nghiệm của phương trình (3).

– Với x < -3 thì phương trình (3) ⇔ -x – 3 = 3x – 1 ⇔ 4x = -2 ⇔ x = -1/2.

Giá trị x = -1/2 không thỏa mãn điều kiện x < -3 nên không phải nghiệm của (3).

– Kết luận: Phương trình có một nghiệm x = 2.

d) |x – 4| + 3x = 5 (4)

– Ta có: |x – 4| = x – 4 nếu x ≥ 4

|x- 4| = -(x – 4) = 4 – x nếu x – 4 < 0 ⇔ x < 4

– Với x ≥ 4 phương trình (4) ⇔ x – 4 + 3x = 5 ⇔ 4x = 9 ⇔ x = 9/4

x = 9/4 không thỏa mãn điều kiện x ≥ 4 nên không là nghiệm của phương trình (4).

– Với x < 4 Phương trình (4) ⇔ 4 – x + 3x = 5 ⇔ 4 + 2x = 5 ⇔ 2x = 1 ⇔ x=1/2.

x = 1/2 thỏa mãn điều kiện x < 4 nên x = 1/2 là nghiệm của (4).

– Kết luận: Phương trình có nghiệm duy nhất x=1/2.

° Dạng 4: Phương trình có nhiều biểu thức chứa dấu giá trị tuyệt đối dạng |A(x)| + |B(x)| = C(x)

* Phương pháp giải:

• Để giải phương trình có nhiều biểu thức chứa dấu giá trị tuyệt đối dạng |A(x)| + |B(x)| = C(x) (*), (trong đó A(x), B(x) và C(x)là biểu thức chứa x) ta thực hiện như sau:

– Xét dấu các biểu thức chứa ẩn nằm trong dấu giá trị tuyệt đối

– Lập bảng xét điều kiện bỏ dấu GTTĐ

– Căn cứ bảng xét dấu, chia từng khoảng để giải phương trình (sau khi giải được nghiệm đối chiếu nghiệm với điều kiện tương ứng).

* Ví dụ: Giải phương trình: |x + 1| + |x – 3| = 2x – 1

° Lời giải:

– Ta có: |x + 1| = x + 1 nếu x ≥ 1

|x + 1| = -(x + 1) nếu x < 1

– Tương tự: |x – 3| = x – 3 nếu x ≥ 3

|x – 3| = -(x – 3) nếu x < 3

– Từ đó ta có bảng sau:

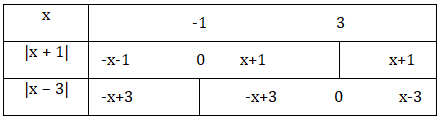
-TH1: Nếu x < -1 thì phương trình (2) trở thành:

-x – 1 – x + 3 = 2x – 1 ⇔ x = 3/4 (không thỏa mãn đk x < -1)

-TH2: Nếu -1 ≤ x ≤ 3 thì phương trình (2) trở thành:

x + 1 – x + 3 = 2x – 1 ⇔ x = 5/2 (thỏa điều kiện -1 ≤ x ≤ 3)

-TH3: Nếu x > 3 thì phương trình (2) trở thành:

x + 1 + x – 3 = 2x – 1 ⇔ 0x = 1 (vô nghiệm)

– Kết luận: Phương trình có nghiệm duy nhất x = 5/2.

° Dạng 5: Phương trình có nhiều biểu thức chứa dấu giá trị tuyệt đối dạng |A(x)| + |B(x)| = |A(x) + B(x)|

* Phương pháp giải:

• Để giải pt trị tuyết đối dạng |A(x)| + |B(x)| = |A(x) + B(x)| ta dựa vào tính chất:

|A(x) + B(x)| ≤ |A(x)| + |B(x)| nên phương trình tương đương với điều kiện đẳng thức A(x).B(x) ≥ 0.

* Ví dụ 1: Giải phương trình sau: |x + 5| + |3 – x| = 8

° Lời giải:

– Ta có: 8 = |x + 5 + 3 – x| ≤ |x + 5| + |3 – x|, ∀x ∈ R.

– Nên |x + 5| + |3 – x| = 8 ⇔ (x + 5)(3 – x) ≥ 0.

– Ta có bảng xét dấu sau:

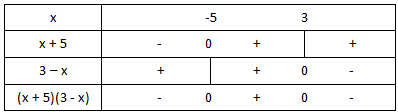
– Từ bảng xét dấu, ta có: (x + 5)(3 – x) ≥ 0 ⇔ -5 ≤ x ≤ 3.

– Vậy bất pt có tập nghiệm là: S = {x ∈ R| -5 ≤ x ≤ 3} hoặc có thể viết S = [-5;3].

* Ví dụ 2: Giải phương trình sau: |5x + 1| + |3 – 2x| = |4 + 3x|

° Lời giải:

– Ta có: |4 + 3x| = |5x + 1 + 3 – 2x| ≤ |5x + 1| + |3 – 2x|. Nên

|5x + 1| + |3 – 2x| = |4 + 3x| ⇔ (5x + 1)(3 – 2x) ≥ 0.

– Ta có bảng xét dấu:

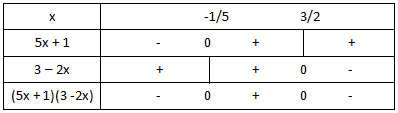
– Từ bảng xét dấu, ta có: (5x + 1)(3 – 2x) ≥ 0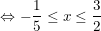 

– Vậy tập nghiệm của bất pt là: .

III. Một số bài tập về phương trình chứa dấu giá trị tuyệt đối

* Giải các phương trình chứa dấu giá trị tuyệt đối sau:

1) |-4x| = x + 2

2) |2 – x| = 2 – 3x

3) 2x – |6x – 7| = -x + 8

4) 

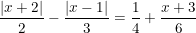
5) |x² – 2x| = x

6) |x² + 4x – 5| = x² – 1

7) 

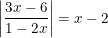
8) 

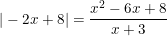
9) 

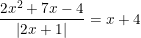
10) |2x + 1| = |x – 1|

11) |1 + 4x| – |7x – 2| = 0

12) |2x² + 5x – 10| = 2x² + 1

13) |x – 2| + |x – 3| = 1

14) |2x + 3| – |x| + x – 1 = 0

15) |x + 1| – 2|x – 1| = x

* Đáp số:

1) S = {-2/5;2/3};

2) S = {0};

3) S = ∅;

4) S = {1/8};

5) S = {0; 1; 3};

6) S = {-3; 1};

7) S = {2};

8) S = {-4/3;4};

9) S = {-4};

10) S = {-2; 0}

11) S = {1/11; 1};

12) S = {-9/4; 1; 11/5};

13) S = [2;3];

14) S = {-1/2};

15) S = {1/2;3/2}.

Hy vọng với bài viết Phương trình chứa dấu Giá trị tuyệt đối và cách giải ở trên giúp ích cho các em. Mọi góp ý và thắc mắc các em hãy để lại nhận xét dưới bài viết để Trường Trung Cấp Nghề Thương Mại Du Lịch Thanh Hoá ghi nhận và hỗ trợ, chúc các em học tốt.

Bản quyền bài viết thuộc Trường Trung Cấp Nghề Thương Mại Du Lịch Thanh Hoá. Mọi hành vi sao chép đều là gian lận!
Nguồn chia sẻ: https://tmdl.edu.vn/phuong-trinh-chua-dau-gia-tri-tuyet-doi/

Trang chủ: tmdl.edu.vn
Danh mục bài: Giáo dục