Sóng cơ là gì? Có bao nhiêu loại sóng và đặc điểm của sóng như thế nào? Mời các em cùng Trường Trung Cấp Nghề Thương Mại Du Lịch Thanh Hoá tìm hiểu sâu hơn về Sóng cơ trong bài học hôm nay. Từ đó giúp các em dễ dàng giải các dạng bài tập Vật li 12 nhé.
Sóng cơ là gì?
Sóng cơ là sự lan truyền truyền dao động cơ (năng lượng, trạng thái dao động) trong một môi trường. Sóng cơ không làm lan truyền phân tử vật chất của môi trường.
Bạn đang xem bài: Sóng cơ là gì? Phân loại sóng và Đặc điểm của Sóng cơ
Sóng cơ chỉ truyền được trong môi trường rắn, lỏng, khí, không truyền được trong chân không. Đây là khác biệt cơ bản giữa sóng cơ và sóng điện từ (sóng điện từ lan truyền rất tốt trong chân không).
Ví dụ: Khi ném một hòn đá xuống mặt nước đang yên ả, trên mặt nước sẽ xuất hiện những gợn tròn lan rộn dần ra đó chính là sóng cơ.
Ví dụ: Trên mặt nước cánh bèo hay chiếc phao chỉ dao động tại chỗ khi sóng truyền qua.
Phân loại sóng
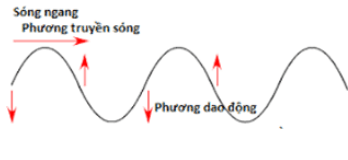
Dựa vào phương dao động của các phần tử và phương lan truyền của sóng người ta phân sóng thành hai loại là sóng dọc và sóng ngang.
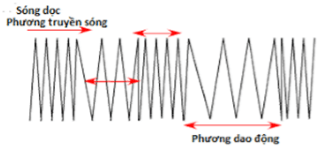
Sóng dọc
Sóng dọc là sóng có phương dao động của các phần tử trùng với phương truyền sóng. Sóng dọc có khả năng lan truyền trong cả 3 trạng thái của môi trường vật chất là Rắn, lỏng, khí.
Nguyên nhân: Trong môi trường lực đàn hồi xuất hiện khi có biến dạng nén, giãn.
Ví dụ: Sóng âm khi truyền trong không khí hay trong chất lỏng là sóng dọc.
Sóng ngang
Sóng ngang là sóng có phương dao động của các phần tử vuông góc với phương truyền sóng. Sóng ngang chỉ có thể lan truyền trong chất rắn và bề mặt chất lỏng, sóng ngang không lan truyền được trong chất lỏng và chất khí.
Nguyên nhân: Trong môi trường lực đàn hồi xuất hiện khi có biến dạng lệch.
Ví dụ: Sóng truyền trên mặt nước là sóng ngang.
Lưu ý:
– Sóng có vận tốc lớn nhất trong chất rắn và nhỏ nhất trong chất khí.
– Các tính chất đặc trưng của sóng: phản xạ, khúc xạ, nhiễu xạ, giao thoa.
Bảng so sánh giữa sóng dọc và sóng ngang
| Sóng ngang | Sóng dọc |
| Các phân tử của môi trường dao động theo phương vuông góc với phương truyền sóng.
Sóng ngang chỉ truyền được trong chất rắn và trên bề mặt chất lỏng. |
Các phần tử của môi trường dao động theo phương trùng với phương truyền sóng.
Sóng dọc truyền trong môi trường rắn lỏng khí. |
| Ví dụ: Sóng trên mặt nước.
|
Ví dụ: Kéo dãn lò xo dọc theo phương của nó rôi thả tay.
|
Các đại lượng đặc trưng của sóng
1. Vận tốc truyền sóng (v): Vận tốc truyền sóng là: v = ΔS/Δt (ΔS là quãng đường sóng truyền trong thời gian Δt).
(Chú ý: Vận tốc sóng là vận tốc lan truyền của sóng trong không gian chứ không phải là vận tốc dao động của các phần tử).
2. Chu kì sóng: T = 2π/ω = 1/f (N là số lần nhô lên của 1 điểm hay số đỉnh sóng đi qua một vị trí hoặc số lần sóng dập vào bờ trong thời gian t(s)).
3. Tần số sóng f: Tất cả các phân tử vật chất trong tất cả các môi trường mà sóng truyền qua đều dao độngcùng một tần số v chu kì, bằng tần số và chu kì của nguồn sóng, gọi là tần số (chu kì) sóng: f = 1/T = ω/2π (Hz)
4. Bước sóng: Bước sóng là quãng đường sóng truyền trong một chu kì. Hoặc là khoảng cách ngắn nhất giữa hai điểm dao động cùng pha trên phương truyền sóng: λ = v.T = v/f (m)
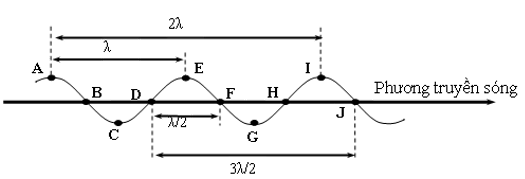
Chú ý: Bất kì sóng nào (với nguồn sóng đứng yên so với máy thu) khi truyền từ môi trường này sang môi trường khác thì bước sóng, năng lượng, vận tốc, biên độ, phương truyền có thể thay đổi nhưng tần số và chu kì thì không đổi và luôn bằng tần số f, chu kì T dao động của nguồn sóng: f = v1/λ1 = v2/λ2 => v1/v2= λ1/λ2 bước sóng trong 1 môi trường tỉ lệ với vận tốc sóng trong môi trường đó.
5. Biên độ sóng: Biên độ sóng tại mỗi điểm là biên độ dao động của phần tử sóng tại điểm đó nói chung trong thực tế biên độ sóng giảm dần khi sóng truyền xa nguồn.
6. Năng lượng sóng Ei: Năng lượng sóng tại mỗi điểm Ei là năng lượng dao động của phần tử sóng tại điểm đó nói chung trong thực tế năng lượng sóng luôn giảm dần khi sóng truyền xa nguồn: Ei = D. ω2.Ai2/2 trong đó D là khối lượng riêng của môi trường sóng, Ai là biên độ sóng tại đó.
Nhận xét: Trong môi trường truyền sóng lý tưởng, ta có bảng nhận xét sau:
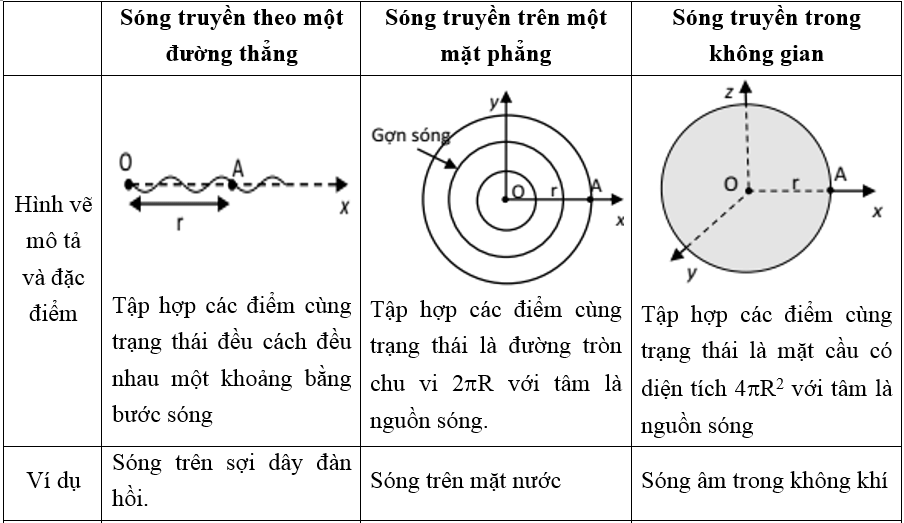
Phương trình sóng
1. Phương trình sóng tại một điểm
* Xét một sóng hình sin đang lan truyền trong một môi trường theo trục Ox, sóng này phát ra từ gốc tọa độ O với phương trình dao động là: uo = Aocos( ωt + φ).
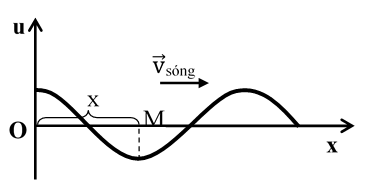
Điểm M cách O một khoảng x. Sóng từ O truyền đến M mất khoảng thời gian ∆t = x/v.
Phương trình dao động của M là:
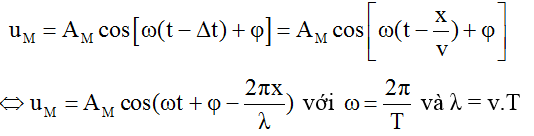
Nếu bỏ qua mất mát năng lượng trong quá trình truyền sóng thì biên độ sóng tại O và M bằng nhau: Ao = AM = A thì:
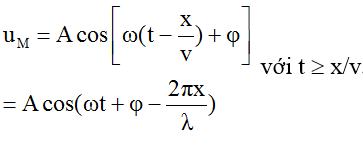
Chú ý: Phương trình sóng truyền theo chiều âm trục Ox đến điểm N có tọa độ x là:
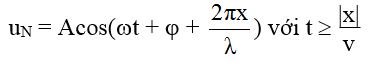
2.Tổng quát
Tại điểm O: uo = Acos( ωt + j) (ở đây O là gốc tọa độ nhưng không phải là nguồn sóng)
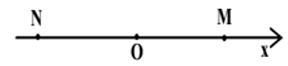
* Tại điểm M cách O một đoạn x trên phương truyền sóng.
+ Nếu sóng truyền theo chiều dương của trục Ox thì:
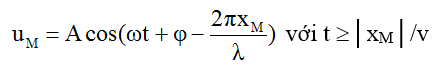
+ Sóng truyền theo chiều âm của trục Ox thì:
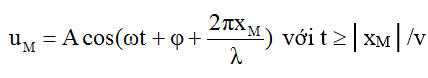
+ Tại một điểm M xác định trong môi trường sóng: x = const; uM là hàm điều hòa theo t với chu kỳ T.
+ Tại một thời điểm xác định t = const ; uM là hàm biến thiên điều hòa theo không gian x với chu kỳ λ.
Chú ý:
+ Tập hợp các điểm cùng khoảng cách đến nguồn sóng đều dao động cùng pha!
+ Nếu tại thời điểm t < |xM|/v thì li độ dao động điểm M luôn bằng 0 (uM = 0) vì sóng chưa truyền đến M.
3. Độ lệch pha 2 điểm M1, M2 do cùng 1 nguồn truyền đến
Phương trình dao động tại nguồn là: u = a.cos(ωt + Φ).
– Phương trình dao động của nguồn truyền đến M1: u1M = a.cos(ωt + Φ – 2πd1/λ) với t ≥ d1/v
– Phương trình dao động của nguồn truyền đến M2: u2M = a.cos(ωt + Φ – 2πd2/λ) với t ≥ d2/v
– Độ lệch pha giữa M1 và M2 là: ΔΦ = 2π/λ.(d2 – d1)
– Để hai dao động cùng pha thì ΔΦ = 2kπ => (d2 – d1) = 2kπ => (d2 – d1) = k.λ
– Để hai dao động ngược thì ΔΦ = (2k+1)π
=> .(d2 – d1) = (2k + 1)π => (d2 – d1) = (k + 0,5)λ
Vậy khoảng cách giữa hai điểm trên phương truyền sóng lệch pha nhau góc ΔΦ (rad) là: L = ΔΦ/2π.λ
=> Trong hiện tượng truyền sóng, khoảng cách ngắn nhất trên phương truyền sóng giữa hai điểm dao động cùng phaa là 1λ, dao động ngược pha là λ/2, dao động vuông pha là λ/4 và dao động lệch pha nhau π/4 là λ/8.
Lưu ý:
+ Đơn vị của x, x1, x2, d, l và v phải tương ứng với nhau.
+ Trong hiện tượng truyền sóng trên sợi dây thép, dây được kích thích dao động bởi nam châm điện với tần số dòng điện là f thì tần số dao động của dây là 2f → fsóng = 2f.
Cách giải Bài tập xác định li độ, vận tốc, trạng thái của phần tử trong Sóng cơ
Phương pháp giải bài tập về Sóng cơ
Xét bài toán yêu cầu tính li độ tại N khi biết li độ tại M, 2 điểm MN cách nhau 1 đoạn là d và M nằm trước N so với nguồn.
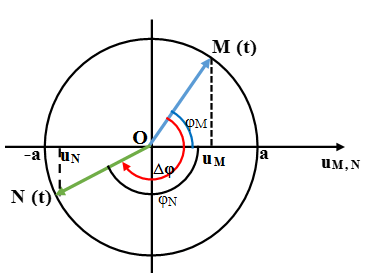
– Bước 1: Xác định độ lệch pha giữa 2 điểm M, N: ΔφMN = 2πdMN/λ
– Bước 2: Xác định pha dao động của M.
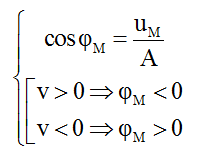
– Bước 3: Từ M trên đường tròn lượng giác, quay theo chiều kim đồng hồ 1 góc ΔφMN để tìm pha của N (ΔφN) (vì dao động tại M sớm pha hơn dao động tại N).
– Bước 4: Xác định li độ dao động của N: uN = A.cosφN
Lưu ý: Khi đề bài cho vận tốc, gia tốc,…ta chuyển về li độ và làm tương tự hoặc có thể sử dụng trực tiếp vòng tròn lượng giác biểu diễn vận tốc, gia tốc.
Ví dụ minh họa về Sóng cơ
Ví dụ 1: Một sóng cơ học lan truyền trên mặt thoáng chất lỏng nằm ngang với tần số 10 Hz, tốc độ truyền sóng 1,2 m/s. Hai điểm M và N thuộc mặt thoáng, trên cùng một phương truyền sóng, cách nhau 26 cm (M nằm gần nguồn sóng hơn). Tại thời điểm t, điểm N hạ xuống thấp nhất. Khoảng thời gian ngắn nhất sau đó điểm M hạ xuống thấp nhất là:
A. 11/120 (s)
B. 1/60 (s)
C. 1/120 (s)
D. 1/12 (s)
Hướng dẫn giải:
Chọn D
Bước sóng λ = v/f = 0,12m = 12cm.
Độ lệch pha giữa 2 điểm M, N: ΔφMN = 2πdMN/λ = 2&pi.26/12 = 4π + π/3 rad
Vì M nằm gần nguồn sóng hơn nên M dao động sớm pha hơn N góc π/3.
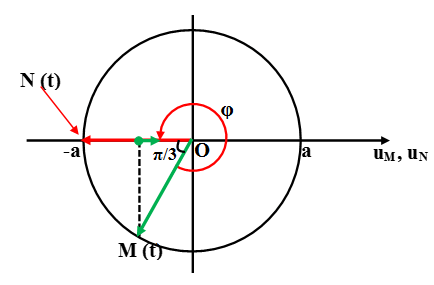
Tại thời điểm t, ta có N hạ xuống thấp nhất, M đang đi lên, sau đó một khoảng thời gian ∆t thì M sẽ hạ xuống thấp nhất:
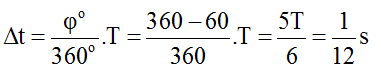
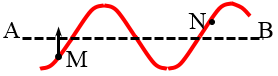
Ví dụ 2: Một sóng truyền theo phương AB. Tại một thời điểm nào đó, hình dạng sóng được biểu diễn trên hình vẽ. Biết rằng điểm M đang đi lên vị trí cân bằng. Khi đó điểm N đang chuyển động như thế nào?
A. Đang đi lên.
B. Đang nằm yên.
C. Không đủ điều kiện để xác định.
D. Đang đi xuống.
Hướng dẫn giải:
Chọn A
Vì M đang đi lên nên ta hiểu rằng: sóng truyền theo hướng từ B sang A, khi đó điểm N sẽ di lên. (Để dễ hiểu nhất ta hãy tưởng tượng một sợi dây thép có dạng như hình vẽ, sau đó ta kéo sang trái thì điểm N phải trượt lên)
Ví dụ 3: Một sóng cơ lan truyền trên một sợi dây rất dài với biên độ không đổi với chu kì T. Ba điểm A, B và C nằm trên sợi dây sao cho B là trung điểm của AC. Tại thời điểm t1, li độ của ba phần tử A, B, C lần lượt là 5,4 mm; 0 mm; 5,4 mm. Nếu tại thời điểm t2 li độ của A và C đều bằng +7,2mm, thì li độ của phần tử tại B tại thời điểm t2 + T/12 có độ lớn là:
A. 10,3 mm.
B. 4,5 mm.
C. 9 mm.
D. 7,8 mm.
Hướng dẫn giải:
Chọn D
Không mất tính tổng quát ta biểu diễn hai thời điểm như trên hình vẽ.
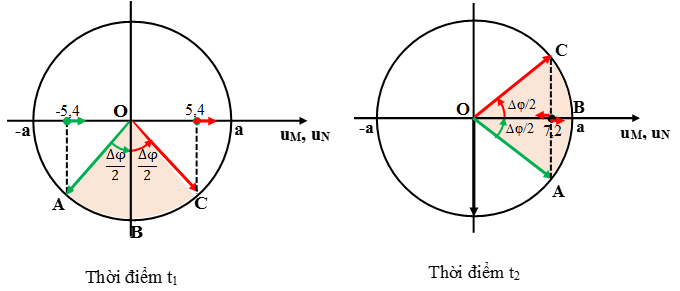
Vì độ lệch pha của dao động tại A, B, C không đổi tại mọi thời điểm nên từ hình vẽ ta có:
Tại thời điểm t1: sin Δφ/2 = 5,4/a
Tại thời điểm t2: cos Δφ/2 = 7,2/a
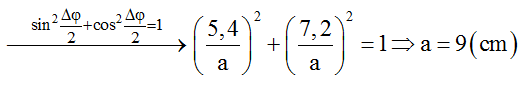
Tại thời điểm t3 = t2 + T/12, tức là sau thời điểm t2, vectơ OB quét thêm góc:
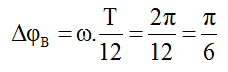
Suy ra li độ của phần tử tại B: uB = acos(π/6) = 9cos(π/6) = 7,8cm.
Ví dụ 4: Cho sóng cơ ổn định, truyền trên một sợi dây rất dài từ một đầu. Tốc độ truyền sóng trên dây là 2,4 m/s, tần số sóng là 20 Hz, biên độ sóng là 4 mm. Hai điểm M và N trên dây cách nhau 37 cm, sóng truyền từ M đến N. Tại thời điểm t, sóng tại M có li độ -2 mm và đang đi về vị trí cân bằng. Vận tốc sóng tại N ở thời điểm t – 1,1125s là:
A. 16π cm/s
B. -8√3 cm/s
C. 80√3 mm/s
D. -8π cm/s
Hướng dẫn giải:
Chọn B
Bước sóng của sóng λ = v/f = 12cm
Độ lệch pha dao động giữa hai điểm M và N là: ΔφMN = 2πdMN/λ = 37π/6 = 6π + π/6
Sóng truyền từ M đến N nên M dao động sớm pha hơn N góc π/6.
Sử dụng vòng tròn lượng giác ta vẽ các vectơ quay biểu diễn dao động tại M và N:
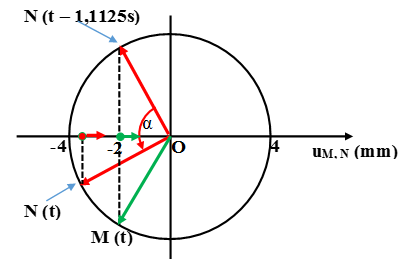
Thời điểm t – 1,1125s ứng với góc lùi: α = 2πft = 44π + π/2
Từ hình vẽ ta xác định được tại thời điểm t – 1,1125s, phần tử N có li độ uN = -2mm và đang đi xuống theo chiều âm (vN < 0).
Vận tốc của M khi đó là:
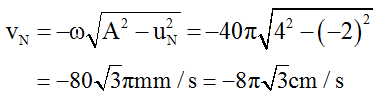
Bài tập vận dụng về Sóng cơ
Câu 1: Một dao động lan truyền trong môi trường liên tục từ điểm M đến điểm N cách M một đoạn 7λ/3 cm. Sóng truyền với biên độ A không đổi. Biết phương trình sóng tại M có dạng uM = 3cos2πt (uM tính bằng cm, t tính bằng giây). Vào thời điểm t1 tốc độ dao động của phần tử M là 6 cm/s thì tốc độ dao động của phần tử N là:
A. 3π (cm/s).
B. 0,5π (cm/s).
C. 4π(cm/s).
D. 6π(cm/s).
Hướng dẫn giải:
Chọn A
Độ lệch pha dao động giữa hai điểm M và N là:
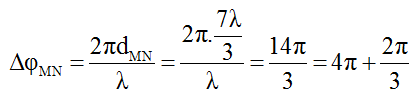
Suy ra vận tốc dao động của M sớm pha hơn N góc 2π/3 rad.
Ta có: uM = 3cos2πt (cm) → vM = 6πcos(2πt + π/2) (cm/s).
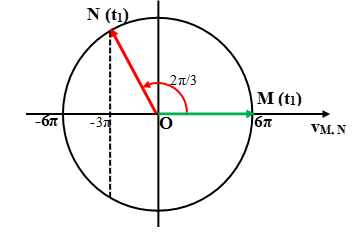
Sử dụng vòng tròn lượng giác ta vẽ các vectơ quay biểu diễn vận tốc tại M và N:
Ta thấy tại thời điểm t1 N có vận tốc: vN = -3π cm/s.
Câu 2: Một sóng ngang truyền trên một sợi dây rất dài. Hai điểm PQ = 9λ/4 sóng truyền từ P đến Q. Những kết luận nào sau đây đúng?
A. Khi Q có li độ cực đại thì P có vận tốc cực đại.
B. Li độ P, Q luôn trái dấu.
C. Khi P có li độ cực đại thì Q có vận tốc cực tiểu.
D. Khi P có thế năng cực đại thì Q có thế năng cực tiểu (chọn mốc thế năng ở vị trí cân bằng).
Hướng dẫn giải:
Chọn D
Độ lệch pha dao động giữa hai điểm P và Q là:
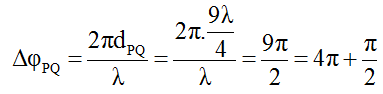
Sóng truyền từ P đến Q nên P dao động sớm pha hơn Q một góc π/2.
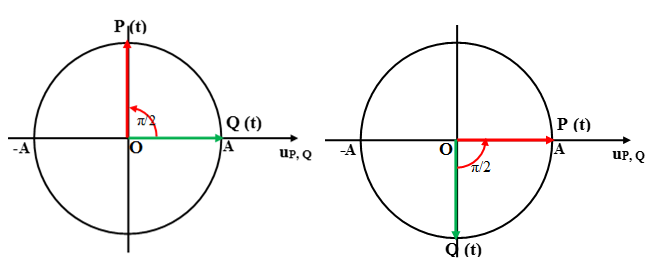
Khi Q có li độ cực đại thì P qua vị trí cân bằng theo chiều âm (v < 0), suy ra A và B sai.
Vì sóng truyền từ P đến Q nên khi P có li độ cực đại thì Q có vận tốc cực đại => C sai
Khi P có thế năng cực đại (P ở vị trí biên) thì Q có thế năng cực tiểu (Q ở vị trí cân bằng)
=> D đúng.
Câu 3: Trên sợi dây có ba điểm M, N và P khi sóng chưa lan truyền thì N là trung điểm của MP. Khi sóng truyền từ P đến M với biên độ không đổi thì vào thời điểm t1 M và P là hai điểm gần nhau nhất mà các phần tử tại đó có li độ tương ứng là –6 mm và +6 mm vào thời điểm kế tiếp gần nhất t2 = t1 + 0,75s thì li độ của các phần tử tại M và P đều là +8 mm. Tốc độ dao động của phần tử N vào thời điểm t1 có giá trị gần đúng nhất là?
A. 4,5 cm/s
B. 2,1 cm/s
C. 1,4 cm/s
D. 8 cm/s.
Hướng dẫn giải:
Chọn B
Sử dụng vòng tròn lượng giác biểu diễn li độ dao động tại M, N và P ở hai thời điểm t1 và t2 (lưu ý sóng truyền từ P đến M nên vectơ OP quay trước vectơ OM).
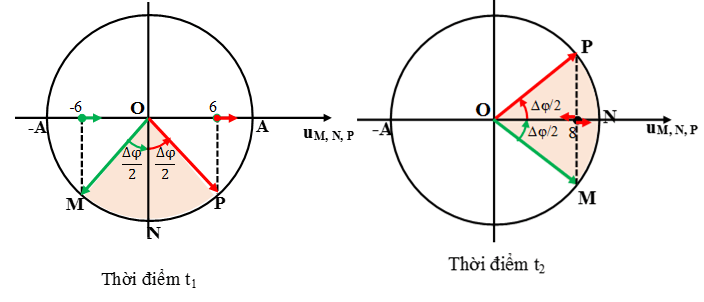
Vì độ lệch pha của dao động tại M, N, P không đổi tại mọi thời điểm nên từ hình vẽ ta có:
Tại thời điểm t1: sin Δφ/2 = 6/a
Tại thời điểm t2: cos Δφ/2 = 8/a
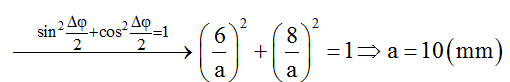
Thời điểm kế tiếp gần nhất t2 = t1 + 0,75s, tức là sau thời điểm t1, vectơ ON quét thêm góc ∆φN = π/2 (do N đi từ cân bằng ra biên dương)
Mặt khác: ΔφN = ω.0,75 = π/2 → ω = 2π/3 rad/s
Vào thời điểm t1, phần tử N đang đi qua vị trí cân bằng nên có tốc độ cực đại:
vN = vmax = ω.A = 20π/3 mm/s = 2,09 cm/s
Câu 4: Sóng ngang có tần số 20 Hz truyền trên mặt nước với tốc độ 2 m/s. Trên một phương truyền sóng đến điểm M rồi mới đến N cách nó 21,25cm. Tại thời điểm t, điểm M hạ xuống thấp nhất thì sau thời gian ngắn nhất bao nhiêu thì điểm N sẽ hạ xuống thấp nhất?
A. 3/400s.
B. 0,0425s.
C. 1/80s.
D. 3/80s.
Hướng dẫn giải:
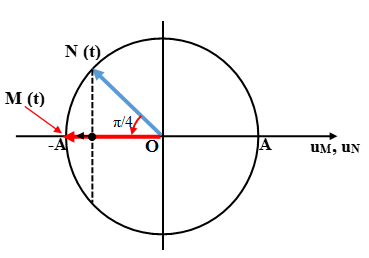
Chọn C
Bước sóng: λ = v/f = 200/20 = 10 cm
Dao động tại M sớm pha hơn tại N (M quay trước N):
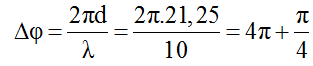
Hiện tại điểm M hạ xuống thấp nhất (hình chiếu ở biên âm) nên M và N phải ở các vị trí như trên vòng tròn.
Để N sẽ hạ xuống thấp nhất (N ở biên âm) thì nó phải quay thêm một góc ∆φ = π/4 rad, tương ứng với thời gian: ∆t = T/4 = 1/80s.
Câu 5: Một sóng cơ lan truyền trên sợi dây từ C đến B với chu kì T = 2 s, biên độ không đổi. Ở thời điểm t1, li độ các phần tử tại B và C tương ứng là – 20 mm và + 20 mm; các phần tử tại trung điểm D của BC đang ở vị trí cân bằng. Ở thời điểm t2, li độ các phần tử tại B và C cùng là +8 mm. Tại thời điểm t3 = t2 + 0,4 s li độ của phần tử D có vận tốc gần nhất với giá trị nào sau đây?
A. – 64,36 mm/s.
B. 67,93 mm/s.
C. -67,93 mm/s.
D. 93,67 mm/s.
Hướng dẫn giải:
Chọn A
Sử dụng vòng tròn lượng giác biểu diễn li độ dao động tại B, D và C ở hai thời điểm t1 và t2 (lưu ý sóng truyền từ C đến B nên vectơ OC quay trước vectơ OB).
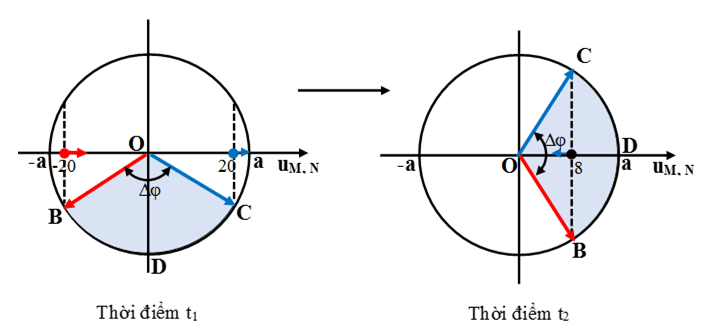
Vì độ lệch pha của dao động tại M, N, P không đổi tại mọi thời điểm nên từ hình vẽ ta có:
Tại thời điểm t1: sin Δφ/2 = 20/a
Tại thời điểm t2: cos Δφ/2 = 8/a
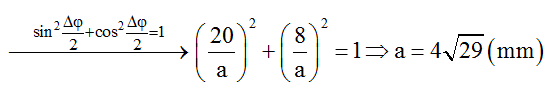
Thời điểm t3 = t2 + 0,4s, tức là sau thời điểm t2 (D ở biên dương), vectơ OD quét thêm góc ∆φD = ω.0,4 = 2π/5 rad = 72o.
Như vậy tại thời điểm t3, D có li độ uD = a.cos72o và đang đi theo chiều âm. Vận tốc của phần tử D khi đó là:
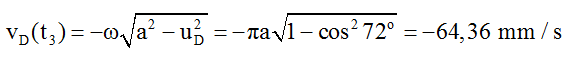
Câu 6: Có hai điểm M và N trên cùng một phương truyền của sóng trên mặt nước, cách nhau 5,75λ (λ là bước sóng). Tại một thời điểm t nào đó, mặt thoáng ở M cao hơn vị trí cân bằng 9mm và đang đi lên; còn mặt thoáng ở N thấp hơn vị trí cân bằng 12mm và đang đi lên. Coi biên độ sóng không đổi. Biên độ sóng a và chiều truyền sóng là
A. 13 mm, truyền từ M đến N
B. 15 mm, truyền từ N đến M
C. 15 mm, truyền từ M đến N
D. 13 mm, truyền từ N đến M
Hướng dẫn giải:
Chọn B
Độ lệch pha của M và N là: Δφ = 2πdMN/λ = 2π.5,75λ/λ = 10π + 3π/2
Suy ra M dao động vuông pha so với N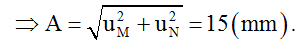 
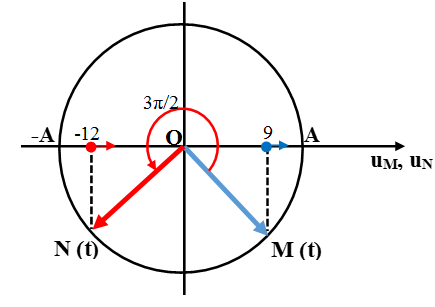
Sử dụng vòng tròn lượng giác biểu diễn li độ dao động tại M và N ở thời điểm t.
Ở thời điểm hiện tại có uM = 9mm (đang đi lên, tức là đi theo chiều dương) và uN = -12mm (đang đi lên, tức là đi theo chiều dương) nên M và N phải ở các vị trí như trên vòng tròn.
Ta thấy, vectơ quay ON chạy trước nên N sớm pha hơn M, tức là sóng truyền qua N rồi mới đến M => Chọn B.
Câu 7: Lúc t = 0, đầu O của sợi dây cao su bắt đầu dao động đi lên với chu kì 2 s. Biên độ 5 cm, tạo thành sóng lan truyền trên dây với tốc độ 2 m/s. Điểm M trên dây cách O một đoạn 1,4 m. Thời điểm đầu tiên để phần tử tại M đến vị trí thấp hơn vị trí cân bằng 2,5 cm xấp xỉ bằng
A. 1,17s.
B. 25s.
C. 1,87s.
D. 0,7s.
Hướng dẫn giải:
Chọn C
+ Bước sóng của sóng: λ = v.T = 4m
Sóng truyền từ O đến M, nên M bắt đầu dao động đi lên từ VTCB vào thời điểm:
t1 = d/v = 1,4/2 = 0,7s
Sau đó M dao động điều hòa với biên độ A = 5cm.
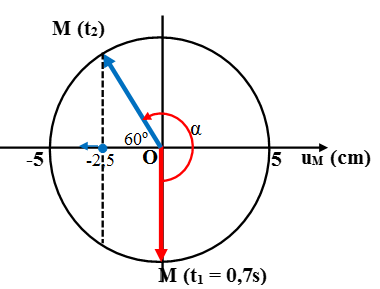
+ Khoảng thời gian kể từ khi M bắt đầu đi lên cho tới khi M đến vị trí thấp hơn vị trí cân bằng 2,5 cm ứng với góc quét: α = 180o + 30o = 210o
Khoảng thời gian tương ứng là: Δt = 210o/360oT = 7/6s
Thời điểm đầu tiên để phần tử tại M đến vị trí thấp hơn vị trí cân bằng 2,5 cm là:
t2 = t1 + ∆t = 0,7 + 7/6 = 1,87s
Câu 8: Hai điểm M, N cùng nằm trên một hướng truyền sóng và cách nhau một phần ba bước sóng. Biên độ sóng không đổi trong quá trình truyền. Tại một thời điểm, khi li độ dao động của phần tử tại M là 3 cm thì li độ dao động của phần tử tại N là 3 cm. Biên độ sóng bằng?
A. 6cm
B. 3cm
C. 2√3cm
D. 3√2cm
Hướng dẫn giải:
Chọn C
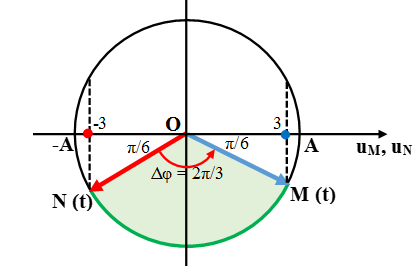
Bài toán không nói rõ sóng truyền theo hướng nào nên ta giả sử truyền qua M rồi mới đến N và biểu diễn như hình vẽ.
Dao động tại N trễ pha hơn hơn M:
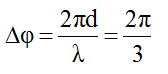
Từ hình vẽ ta tìm được biên độ A:
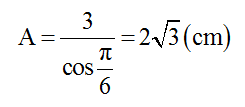
Câu 9: Sóng cơ lan truyền qua điểm M rồi đến điểm N cùng nằm trên một phương truyền sóng cách nhau d = 5λ/3 . Tại thời điểm t có uM = +4cm và uN = -4cm. Thời điểm gần nhất để uM = 2cm là:
A. t2 = t1 + T/3.
B. t2 = t1 + 0,262T
C. t2 = t1 + 0,095T
D. t2 = t1 + T/12
Hướng dẫn giải:
Chọn C
Dao động M sớm pha hơn tại N (M quay trước N):
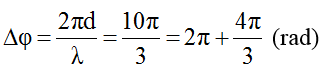
Tại thời điểm t = t1 có uM = +4cm và uN = -4cm nên M và N phải ở các vị trí như trên vòng tròn.
Từ hình vẽ ta tìm được biên độ:
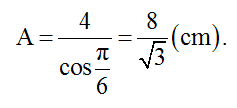
Để M có li độ 2cm thì nó phải quay thêm một góc:
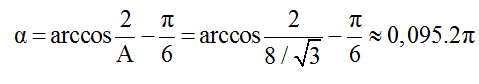
Tương ứng với thời gian: ∆t = 0,095T => Chọn C.
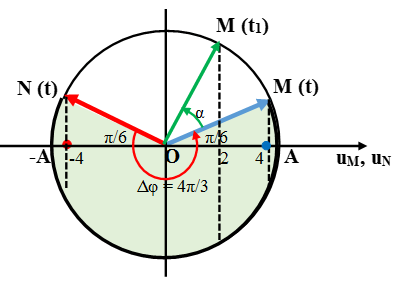
Câu 10: Tại thời điểm đầu tiên t = 0, đầu O của sợi dây cao su căng thẳng nằm ngang bắt đầu dao động đi lên với tần số 2,5 Hz. Gọi P, Q là hai điểm cùng nằm trên một phương truyền sóng cách O lần lượt là 8 cm và 16 cm. Biết vận tốc truyền sóng trên dây là 24 cm/s và coi biên độ sóng không đổi khi truyền đi. Hỏi sau thời gian ngắn nhất là bao lâu thì O, P, Q thẳng hàng?
A. 0,16 s.
B. 0,25 s.
C. 0,56 s.
D. 0,2 s.
Hướng dẫn giải:
Chọn D
Bước sóng: λ = v/f = 24/2,5 = 12cm.
Chu kì sóng: T = 1/f = 0,4s.
Thời gian cần thiết để sóng truyền từ O đến P và O đến Q lần lượt là:
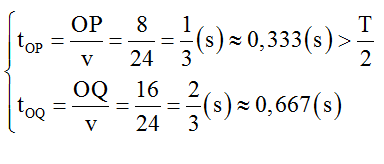
Ở thời điểm t = T/2 = 0,2s điểm O trở về vị trí cân bằng và sóng mới truyền được một đoạn λ/2 = 6cm, nghĩa là chưa truyền đến P (cả P và Q đều chưa dao động) tức là lúc này O, P và Q thẳng hàng Chọn D.
Câu 11: Một sóng cơ học lan truyền trên mặt thoáng chất lỏng nằm ngang với tần số 10 Hz, tốc độ truyền sóng 1,2 m/s. Hai điểm M và N thuộc mặt thoáng, trên cùng một phương truyền sóng, cách nhau 26 cm (M nằm gần nguồn sóng hơn). Tại thời điểm t, điểm N hạ xuống thấp nhất. Khoảng thời gian ngắn nhất sau đó điểm M lên cao nhất là:
A. 11/120s.
B. 1/60s.
C. 1/120s.
D. 1/30s.
Hướng dẫn giải:
Chọn D
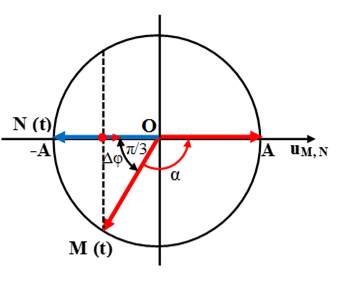
Bước sóng: λ = v/f = 1,2/10 = 0,12m = 12cm
Dao động tại M sớm pha hơn tại N (M quay trước N):
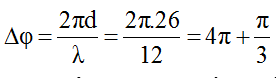
Thời điểm t, N hạ xuống thấp nhất (N ở biên âm) nên N và M ở các vị trí như trên vòng tròn.
Để M lên cao nhất (M ở biên dương) thì nó phải quay thêm một góc: α = 2π/3 rad, tương ứng với khoảng thời gian .
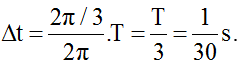
Câu 12: Sóng ngang truyền trên mặt nước với bước sóng 0,1m. Sóng đến điểm M rồi mới đến N cách nó 21,5 cm. Thời gian truyền sóng từ M đến N là 2,15s. Tại thời điểm t, điểm N hạ xuống thấp nhất thì sau thời gian ngắn nhất bao nhiêu thì điểm M sẽ hạ xuống thấp nhất?
A. 17/20s.
B. 7/20s.
C. 1/20s.
D. 3/20s.
Hướng dẫn giải:
Chọn A
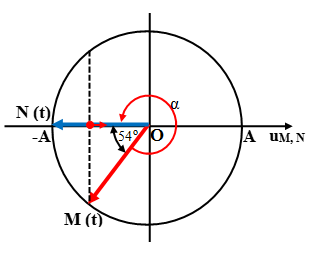Do vậy M sớm pha hơn N góc ∆φ = rad = 54o
Tốc độ truyền sóng: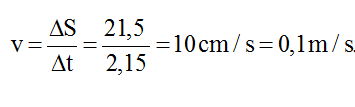 
Chu kì sóng: T = λ/v = 1s
Dao động tại M sớm pha hơn tại N (M quay trước N):
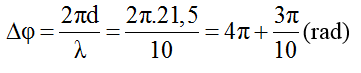
Do vậy M sớm pha hơn N góc ∆φ = 3π/10 rad = 54o
Thời điểm t, N hạ xuống thấp nhất (N ở biên âm) nên N và M ở các vị trí như trên vòng tròn.
Để M hạ xuống thấp nhất (M ở biên âm) thì nó phải quay thêm một góc:
α = 360o – 54o = 306o, tương ứng với khoảng thời gian:
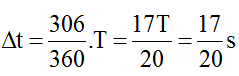Do vậy M sớm pha hơn N góc ∆φ = rad = 54o
Câu 13: Một sóng cơ lan truyền trên một sợi dây rất dài từ M đến P với biên độ không đổi với chu kì T. Ba điểm M, N và P nằm trên sợi dây sao cho N là NP = -3NM . Tại thời điểm t1, li độ của ba phần tử M, N, P lần lượt là -5√3 mm; uN1 mm; 5√3 mm. Nếu tại thời điểm t2 li độ của M và P đều bằng +5 mm, thì li độ của phần tử tại N tại thời điểm t2 + T/24 có độ lớn là:
A. 4√3 mm.
B. 5√3 mm.
C. 5√2 mm.
D. 10 mm.
Hướng dẫn giải:
Chọn C
Vì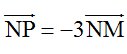 
nên N nằm giữa M và P sao cho NM = 1/4MP
M dao động sớm pha hơn P một góc: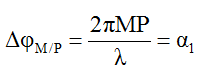 
M dao động sớm pha hơn N một góc: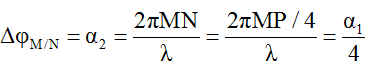 
Sử dụng vòng tròn lượng giác biểu diễn li độ dao động tại M, N, P, C (trung điểm MP) ở hai thời điểm t1 và t2 (lưu ý sóng truyền từ M đến P nên vectơ OM quay trước vectơ OP).
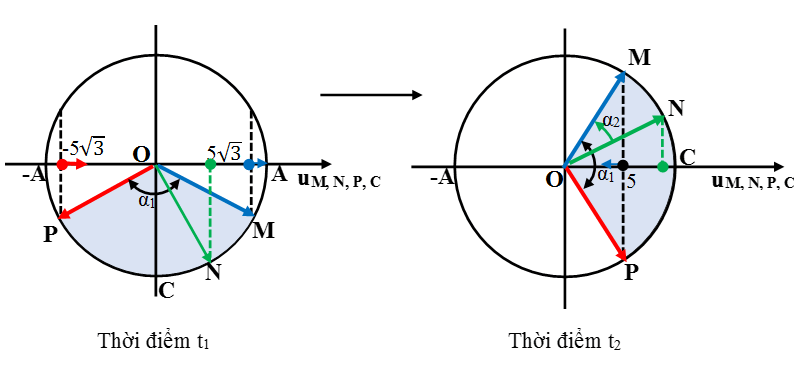
Vì độ lệch pha của dao động tại M, N, C, P không đổi tại mọi thời điểm nên từ hình vẽ ta có:
Tại thời điểm t1: sin α1/2 = 5√3/A
Tại thời điểm t2: sin α1/2 = 5/A
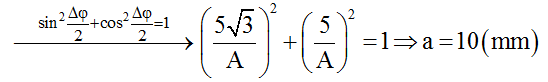
Suy ra α1 = 120o; α2 = 30o → ở thời điểm t2, trên hình vẽ
Thời điểm t3 = t2 + T/24 s, tức là sau thời điểm t2, vectơ ON quét thêm góc ∆φN = 15o.
Như vậy tại thời điểm t3, ∠NOC = 30 + 15 = 45o , do đó N có li độ uN = A.cos45o = 5√2 mm.
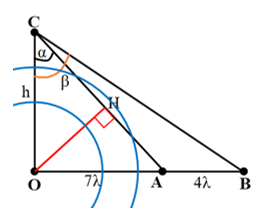
Câu 14: Một sóng hình sin lan truyền trên mặt nước từ nguồn O với bước sóng λ. Ba điểm A, B, C trên hai phương truyền sóng sao cho OA vuông góc với OC và B là một điểm thuộc tia OA sao cho OB > OA. Biết OA = 7λ. Tại thời điểm người ta quan sát thấy giữa A và B có 5 đỉnh sóng (kể cả A và B) và lúc này góc ∠ACB đạt giá trị lớn nhất. Số điểm dao động ngược pha với nguồn trên đoạn AC bằng
A. 4.
B. 5.
C. 6.
D. 7.
Hướng dẫn giải:
Chọn C.
Giữa A và B có 5 đỉnh sóng với A, B cũng là đỉnh sóng →AB = 4λ.
Ta có:
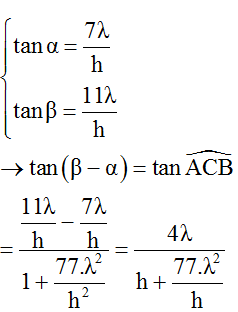
Từ biểu thức trên ta thấy góc ∠ACB lớn nhất khi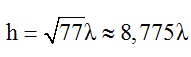 
Dựng đường cao OH, ta có:
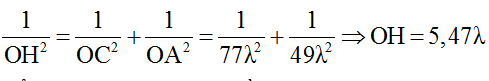
Gọi M là một điểm trên AC, để M ngược pha với nguồn thì
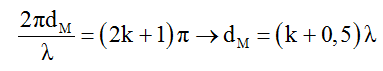
+ Điểm M ngược pha với nguồn trên đoạn HC thỏa mãn:
OH ≤ dM ≤ OC ↔ 5,47 ≤ k + 0,5 ≤ 8,775
↔ 4,97 ≤ k ≤ 8,275. Suy ra trên HC có ta 4 vị trí thỏa mãn.
+ Điểm M ngược pha với nguồn trên đoạn HA thỏa mãn:
OH < dM ≤ OA ↔ 5,47 ≤ k + 0,5 ≤ 7
↔ 4,97 ≤ k ≤ 6,5. Suy ra trên HA có 2 vị trí thỏa mãn.
Vậy trên AC có 6 vị trí của M ngược pha với nguồn.
************
Trên đây là toàn bộ kiến thức về lý thuyết sóng cơ cùng các bài tập vận dụng về Sóng cơ. Với các kiến thức bài học trên sẽ giúp học sinh dễ dàng giải các dạng bài và luyện tập kiến thức lý thuyết cũng như bài tập lớp 12 Vật lý dễ dàng hơn.
Đăng bởi: Trường Trường Trung Cấp Nghề Thương Mại Du Lịch Thanh Hoá
Chuyên mục: Giáo Dục
Bản quyền bài viết thuộc Trường Trung Cấp Nghề Thương Mại Du Lịch Thanh Hoá. Mọi hành vi sao chép đều là gian lận!
Nguồn chia sẻ: https://tmdl.edu.vn https://tmdl.edu.vn/song-co-la-gi/
Trang chủ: tmdl.edu.vn
Danh mục bài: Giáo dục
