Tim điều kiện m để giá trị của biểu thức nghiệm đạt Giá trị lớn nhất, Giá trị nhỏ nhất. Thầy cô trường Trường Trung Cấp Nghề Thương Mại Du Lịch Thanh Hoá đã chia sẻ với các em bài viết về Cách tìm Giá trị lớn nhất và Giá trị nhỏ nhất của biểu thức cũng như bài viết về Hệ thức Vi-et và ứng dụng giải các bài toán liên quan.
Ở bài viết này, Trường Trung Cấp Nghề Thương Mại Du Lịch Thanh Hoásẽ giới thiệu một dạng toán kết hợp giữa Hệ thức nghiệm Vi-ét và Giá trị lớn nhất, Giá trị nhỏ nhất, đó là: Tìm giá trị m để biểu thức nghiệm đạt giá trị lớn nhất (GTLN), giá trị nhỏ nhất (GTNN).
Bạn đang xem bài: Tim điều kiện m để giá trị của biểu thức nghiệm đạt Giá trị lớn nhất, Giá trị nhỏ nhất – Toán 9 chuyên đề
I. Một số ví dụ tìm m để biểu thức đạt GTLN, GTNN
Để giải bài toán tìm giá trị của m m để biểu thức nghiệm đạt giá trị lớn nhất hay giá trị nhỏ nhất ta vận dụng tính chất sau về bất đẳng thức:
• Trong mọi trường hợp nếu ta luôn phân tích được:
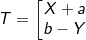(trong đó X, Y là các biểu thức không âm; a, b là hằng số) (*)
– Thì ta thấy:
T≥a (vì X≥0) ⇒ minT = a ⇔ X = 0.
T≤b (vì Y≥0) ⇒ maxT = b ⇔ Y = 0.
* Ví dụ 1: Cho phương trình: x2 + (2m – 1)x – m = 0
Gọi x1, x2 là các nghiệm của phương trình. Tìm m để biểu thức T = x12 + x22 – 6x1x2 đạt giá trị nhỏ nhất.
* Lời giải:
– Theo hệ thức Vi-ét, ta có: x1 + x2 = -b/a = -(2m – 1) và x1.x2 = c/a = -m
– Theo bài ra, ta có:
T = x12 + x22 – 6x1x2
= x12 + 2x1x2 + x22 – 8x1x2
= (x1 + x2)2 – 8x1x2
= (2m – 1)2 + 8m
= 4m2 – 4m + 1 + 8m
= 4m2 + 4m + 1
= (2m + 1)2≥0
Suy ra: minT = 0 ⇔ 2m + 1 = 0 ⇔ m = -1/2.
* Ví dụ 2: Cho phương trình x2 – mx + m – 1 = 0
Gọi x1, x2 là các nghiệm của phương trình. Tìm giá trị nhỏ nhất và giá trị lớn nhất của biểu thức sau:
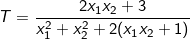
> Lời giải:
– Theo hệ thức Vi-ét, ta có: x1 + x2 = m và x1x2 = m – 1.
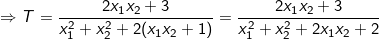
+ Cách 1: Thêm bớt để đưa về dạng như hướng dẫn ở đầu bài viết. Ta biến đổi T như sau:
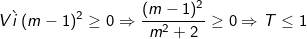
Vậy maxT = 1 ⇔ m – 1 = 0 ⇔ m = 1.
Với cách thêm bớt khác ta có:
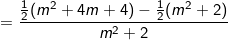
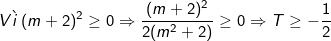
Vậy minT = -1/2 ⇔ m + 2 = 0 ⇔ m = -2.
+ Cách 2: Đưa về giải phương trình bậc 2 với ẩn là m và T là tham số, ta sẽ tìm điều kiện cho tham số T để phương trình đã cho luôn có nghiệm với mọi m.
(**)
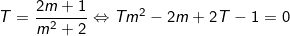Ta có: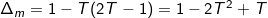 
Để phương trình (**) luôn có nghiệm với mọi m thì Δ≥0, hay:
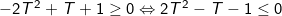
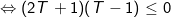
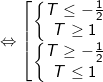
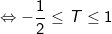
Vậy maxT = 1 ⇔ m = 1; minT = -1/2 ⇔ m = -2.
II. Bài tập vận dụng
* Bài tập 1: Cho phương trình: x2 + (4m + 1)x + 2(m – 4) .Tìm m để biểu thức A = (x1 – x2)2 có giá trị nhỏ nhất.
* Bài tập 2: Cho phương trình x2 – 2(m – 1)x – 3 – m = 0. Tìm m sao cho nghiệm x1, x2 thỏa mãn điều kiện x12 + x22 ≥ 10.
* Bài tập 3: Cho phương trình: x2 – 2(m – 4)x + m2 – 8 = 0 xác định m để phương trình có 2 nghiệm x1, x2 thỏa mãn:
a) A = x1 + x2 – 3x1x2 đạt giá trị lớn nhất
b) B = x12 + x22 – x1x2 đạt giá trị nhỏ nhất
* Bài tập 4: Cho phương trình: x2 – (m + 1)x – m2 + m – 2 = 0. Với giá trị nào của m, biểu thức C = x12 + x22 đạt giá trị nhỏ nhất.
* Bài tập 5: Cho phương trình x2 + (m + 1)x + m = 0 . Xác định m để biểu thức E = x12 + x22 đạt giá trị nhỏ nhất.
Như vậy, với bài viết về tìm điều kiện m để giá trị của biểu thức nghiệm đạt Giá trị lớn nhất, Giá trị nhỏ nhất Trường Trung Cấp Nghề Thương Mại Du Lịch Thanh Hoáhy vọng giúp ích cho các em. Đây cũng là dạng toán hay xuất hiện trong đề thi tuyển sinh lớp 10, vì vậy các em hãy ôn tập thật tốt nhé.
Bản quyền bài viết thuộc Trường Trung Cấp Nghề Thương Mại Du Lịch Thanh Hoá. Mọi hành vi sao chép đều là gian lận!
Nguồn chia sẻ: https://tmdl.edu.vn https://tmdl.edu.vn/tim-dieu-kien-m-de-gia-tri-cua-bieu-thuc-nghiem-dat-gia-tri-lon-nhat-gia-tri-nho-nhat/
Trang chủ: tmdl.edu.vn
Danh mục bài: Giáo dục
