Tìm x để biểu thức nguyên, cách giải và bài tập vận dụng. Bài toán tìm giá trị nguyên của x để biểu thức nhận giá trị nguyên ở toán lớp 7 là một trong những dạng bài tập các em không hay gặp nhiều, vì vậy có nhiều em còn bỡ ngỡ chưa biết cách giải khi gặp dạng này.
Bài này sẽ hướng dẫn các em cách giải dạng toán: Tìm x để biểu thức nguyên, qua đó vận dụng vào giải một số bài tập minh họa để các em dễ hiểu hơn.
Bạn đang xem bài: Tìm x để biểu thức nguyên, cách giải và bài tập vận dụng – Toán lớp 7 chuyên đề
I. Cách giải bài toán: Tìm x để biểu thức nguyên
• Để tìm x để biểu thức nguyên ta cần thực hiện các bước sau:
+ Bước 1: Tìm điều kiện của x (phân số thì mẫu số phải khác 0).
+ Bước 2: Nhận biết dạng bài toán để có cách giải tương ứng
– Nếu tử số không chứa x, ta dùng dấu hiệu chia hết.
– Nếu tử số chứa x, ta dùng dấu hiệu chia hết hoặc dùng phương pháp tách tử số theo mẫu số.
– Với các bài toán tìm đồng thời x, y ta nhóm x hoặc y rồi rút x hoặc y đưa về dạng phân thức.
+ Bước 3: Áp dụng các tính chất để giải quyết bài toán tìm ra đáp án.

II. Bài tập Tìm x để biểu thức nguyên
* Bài tập 1: Tìm x để biểu thức A nhận giá trị nguyên: 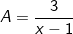
> Lời giải:
– Điều kiện: x – 1 ≠ 0 ⇒ x ≠ 1
– Để A nguyên thì 3 chia hết cho (x – 1) hay (x – 1) là ước của 3
tức là: (x – 1) ∈ Ư(3) = {-3; -1; 1; 3}
Với: x – 1 = -3 ⇒ x = -2
x – 1 = -1 ⇒ x = 0
x – 1 = 1 ⇒ x = 2
x – 1 = 3 ⇒ x = 4
Hoặc ta có thể lập bảng như sau:
| x – 1 | -3 | -1 | 1 | 3 |
| x | -2 | 0 | 2 | 4 |
Các giá trị của x đề thỏa, vậy ta kết luận:
Để A nhận giá trị nguyên thì x thỏa: x ∈ {-2; 0; 2; 4}
* Bài tập 2: Tìm x để biểu thức sau nhận giá trị nguyên: 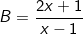
* Lời giải:
– Điều kiện: x ≠ 1
+) Cách 1: Bài toán dạng phân thức tử số chứa biến x, nên ta có thể tách tử số theo mẫu số như sau:
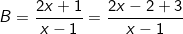
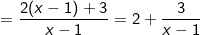
Để B nguyên thì 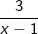 là số nguyên hay 3 chia hết cho (x – 1) hay (x – 1) là ước của 3, tức là: (x – 1) ∈ Ư(3) = {-3; -1; 1; 3}.
là số nguyên hay 3 chia hết cho (x – 1) hay (x – 1) là ước của 3, tức là: (x – 1) ∈ Ư(3) = {-3; -1; 1; 3}.
Theo bài tập 1, ta có:
| x – 1 | -3 | -1 | 1 | 3 |
| x | -2 | 0 | 2 | 4 |
Vậy để B nhận giá trị nguyên thì x thỏa: x ∈ {-2; 0; 2; 4}
+) Cách 2: Dùng dấu hiệu chia hết, các bước làm:
i) Tìm điều kiện.
ii) Tử  mẫu và Mẫu
mẫu và Mẫu  mẫu; nhân thêm hệ số rồi dùng tính chất chia hết một tổng, một hiệu.
mẫu; nhân thêm hệ số rồi dùng tính chất chia hết một tổng, một hiệu.
Ta có: (x – 1) 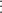 (x – 1) nên 2(x – 1)
(x – 1) nên 2(x – 1) 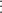 (x – 1) (*)
(x – 1) (*)
Để B nguyên thì (2x + 1) 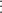 (x – 1) (**)
(x – 1) (**)
Từ (*) và (**) suy ra: (2x + 1) – 2(x – 1) 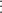 (x – 1)
(x – 1)
⇔ 3 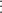 (x – 1) suy ra (x – 1) ∈ Ư(3) = {-3; -1; 1; 3}
(x – 1) suy ra (x – 1) ∈ Ư(3) = {-3; -1; 1; 3}
| x – 1 | -3 | -1 | 1 | 3 |
| x | -2 | 0 | 2 | 4 |
* Bài tập 3: Tim x để biểu thức C nhận giá trị nguyên: 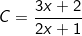
> Lời giải:
– Điều kiện: 2x + 1 ≠ 0 ⇒ x ≠ -1/2 (x ∈ Z)
– Ta có: 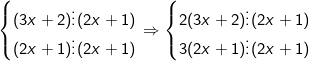
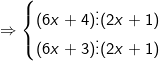
Hay (6x + 4) – (6x + 3) 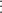 (2x + 1) ⇒ 1
(2x + 1) ⇒ 1 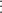 (2x + 1)
(2x + 1)
⇒ (2x + 1) ∈ Ư(1) = {-1; 1}
Với 2x + 1 = -1 ⇒ x = -1 (thỏa)
Với 2x + 1 = 1 ⇒ x = 0 (thỏa)
Vậy với x = 0 (khi đó C = 2) hoặc x = -1 (khi đó C = 1) thì biểu thức C nhận giá trị nguyên.
* Bài tập 4: Tim x để biểu thức D nhận giá trị nguyên: 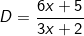
> Lời giải:
– Nhận xét: Ta thấy tử số và mẫu số của D có chứa x, mà hệ số trước x ở tử là 6 lại chia hết cho hệ số trước x ở mẫu là 2, nên ta dùng phương pháp tách tử số thành bội của mẫu số để giải bài này.
– Điều kiện: 2x + 2 ≠ 0 ⇒ x ≠ -1 (x ∈ Z)
– Ta có: 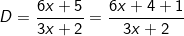
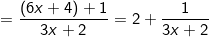
Như vậy để D nguyên thì 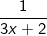 nguyên
nguyên
Suy ra: 1 chia hết cho (3x + 2) hay (3x + 2) ∈ Ư(1) = {-1; 1}
Với 3x + 2 = -1 ⇒ 3x = -3 ⇒ x = -1 (thỏa)
Với 3x + 2 = 1 ⇒ 3x = -1 ⇒ x = -1/3 ∉ Z (loại)
Vậy với x = -1 (khi đó D = 1) thì D nhận giá trị nguyên.
• Tìm giá trị nguyên với biểu thức dạng: ax + bxy + cy = d ta làm như sau:
+ Bước 1: Nhóm các hạng tử xy với x (hoặc y)
+ Bước 2: Đặt nhân tử chung và phân tích hạng tử còn lại theo hạng tử trong ngoặc để đưa về dạng tích.
* Ví dụ: Tìm x, y nguyên sao cho: xy + 3y – 3x = -1
> Lời giải:
– Ta có: y(x + 3) – 3x + 1 = 0 [Nhóm hạng tử chứa xy với hạng tử chứa y và đặt nhân tử chung là y]
⇔ y(x + 3) – 3(x + 3) + 10 = 0 [phân tích -3x + 1 = -3x – 9 + 10=-3(x + 3) +10]
⇔ (x + 3)(y – 3) = -10
Như vậy có các khả năng xảy ra sau:
(x + 3) = 1 thì (y – 3) = -10 ⇒ x = -2 và y = -7
(x + 3) = -10 thì (y – 3) = 1 ⇒ x = -13 và y = 4
(x + 3) = 2 thì (y – 3) = -5 ⇒ x = -1 và y = -2
(x + 3) = -5 thì (y – 3) = 2 ⇒ x = -8 và y = 5
Ta có thể lập bảng dễ tính hơn khi x, y có nhiều giá trị.
| x + 3 | 1 | -10 | 2 | -5 |
| y – 3 | -10 | 1 | -5 | 2 |
| x | -2 | -13 | -1 | -8 |
| y | -7 | 4 | -2 | 5 |
• Tìm giá trị nguyên với biểu thức dạng: (a/x) + (b/y) = c ta quy đồng đưa về dạng: Ax + By + Cxy + D =0.
* Ví dụ: Tìm giá trị nguyên của biểu thức: 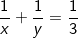
> Lời giải:
– Điều kiện: x ≠ 0, y ≠ 0.
– Ta nhân và quy đòng mẫu số chung là 3xy được:
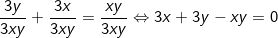
(Bài toán được đưa về dạng ax + by + cxy + d = 0)
⇔ x(3 – y) – 3(3 – y) + 9 = 0
⇔ (x – 3)(3 – y) = -9
Vậy có các trường hợp sau xảy ra:
(x – 3) = 1 thì (3 – y) = -9 ⇒ x = 4 và y = 12 (thỏa đk)
(x – 3) = -1 thì (3 – y) = 9 ⇒ x = 2 và y = -6 (thỏa đk)
(x – 3) = 3 thì (3 – y) = -3 ⇒ x = 6 và y = 6 (thỏa đk)
(x – 3) = -3 thì (3 – y) = 3 ⇒ x = 0 và y = 0 (loại)
* Bài tập luyện tập 1: Tìm x để các biểu thức sau nguyên:
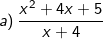
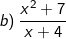
* Bài tập luyện tập 2: Tìm x để các biểu thức sau nguyên:
a) xy + 2x + y = 11
b) 9xy – 6x + 3y = 6
c) 2xy + 2x – y = 8
d) xy – 2x + 4y = 9
Hy vọng với bài viết hướng dẫn cách tìm x để biểu thức nguyên, cách giải và bài tập vận dụng ở giúp các em không còn bỡ ngỡ khi gặp dạng toán này, các em cần ghi nhớ các bước giải để khi gặp dạng toán tương tự để áp dụng nhé.
Bản quyền bài viết thuộc Trường Trung Cấp Nghề Thương Mại Du Lịch Thanh Hoá. Mọi hành vi sao chép đều là gian lận!
Nguồn chia sẻ: https://tmdl.edu.vn/tim-x-de-bieu-thuc-nguyen-cach-giai-va-bai-tap-van-dung/
Trang chủ: tmdl.edu.vn
Danh mục bài: Giáo dục