Vật lý 12 bài 5: Tổng hợp hai Dao động Điều hòa, phương pháp giản đồ FRE NEN và bài tập vận dụng. Trong thực tế một vật thường chịu tác động của nhiều dao động, như màng nhĩ của tai hay màng rung của micro thường xuyên nhận được được nhiều dao động gây ra bởi các sóng âm, vậy tổng hợp của các dao động này sẽ như thế nào?
Nội dung bài viết này sẽ chỉ đề cấp đến việc tổng hợp hai dao động điều hòa cùng phương cùng tần số và phương pháp giản đồ FRE NEN để tổng hợp 2 dao động cùng phương cùng tần số này. Qua đó chúng ta sẽ áp dụng giải một số bài tập để hiểu rõ hơn.
Bạn đang xem bài: Vật lý 12 bài 5: Tổng hợp hai Dao động Điều hòa, phương pháp giản đồ FRE NEN và bài tập vận dụng
I. Vectơ quay
– Khi điểm M chuyển động tròn đều thì vectơ vị trí 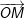 quay đều với cùng tốc độ góc ω. Khi ấy x=Acos(ωt+φ) là phương trình của hình chiếu của vectơ quay
quay đều với cùng tốc độ góc ω. Khi ấy x=Acos(ωt+φ) là phương trình của hình chiếu của vectơ quay 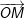 lên trục x.
lên trục x.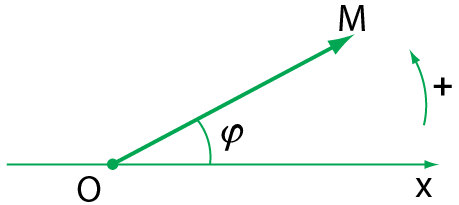 – Dựa vào đó đưa ra cách biểu diễn phương trình của dao động điều hòa bằng một vectơ quay được vẽ tại thời điểm ban đầu như hình minh họa ở trên.
– Dựa vào đó đưa ra cách biểu diễn phương trình của dao động điều hòa bằng một vectơ quay được vẽ tại thời điểm ban đầu như hình minh họa ở trên.
• Vectơ quay có những đặc điểm sau đây:
– Có gốc tại gốc tọa độ của trục Ox
– Có độ dài bằng biên độ dao động, OM = A;
– Hợp với trục Ox một góc bằng pha ban đầu (chọn chiều dương là chiều dương của đường tròn lượng giác).
II. Phương pháp giản đồ FRE-NEN
1. Đặt vấn đề
– Phương pháp giản đồ Fre-nen thường được dùng để tìm li độ của dao động tổng hợp của hai dao động điều hòa cùng phương, cùng tần số nhưng khác biên độ dao động (A1 ≠ A2) như sau:
x1=A1cos(ωt+φ1)
x2=A2cos(ωt+φ2)
2. Phương pháp giản đồ Fre-nen tổng hợp 2 dao động điều hòa
– Vẽ hai vectơ quay 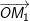 và
và 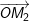 , vẽ vectơ
, vẽ vectơ 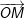 là tổng của hai vectơ
là tổng của hai vectơ 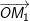 và
và 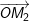 như hình sau:
như hình sau:
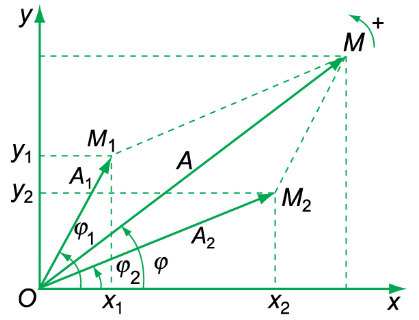
x1 = A1cos(ωt+φ1)
x2 = A2cos(ωt+φ2)
⇒ x = Acos(ωt+φ)
– Như vậy, dao động tổng hợp của hai dao động điều hòa cùng phương, cùng tần số là một dao động điều hòa cùng phương, cùng tần số với hai dao động đó.
– Trong trường hợp tổng quát, biên độ và pha ban đầu của dao động tổng hợp được tính bằng các công thức sau đây:
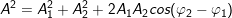
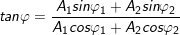
3. Ảnh hưởng của độ lệch pha
– Từ công thức trên ta thấy biên độ của dao động tổng hợp phụ thuộc vào các biên độ A1, A2 và độ lệch pha (φ2-φ1) của các dao động thành phần.
– Nếu các dao động thành phần cùng pha, tức ∆φ = φ2 – φ1 = 2nπ, (n = 0, ±1, ±2,…), thì biên độ dao động tổng hợp là lớn nhất và bằng tổng hai biên độ: A = A1 + A2.
– Nếu hai dao động thành phần ngược pha, tức ∆φ = φ2 – φ1 = (2n+1)π, (n = 0, ±1, ±2,…), thì biên độ dao động tổng hợp là nhỏ nhất: A = |A1 – A2|
4. Ví dụ minh họa phương pháp giản đồ FRE-NEN tổng hợp 2 giao động
– Cho hai dao động điều hòa cùng phương, cùng tần số:
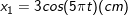
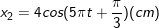
– Tìm phương trình dao động tổng hợp của 2 giao động trên.
* Lời giải: Ta vẽ hai vectơ quay biểu diễn hai dao động thành phần tại thời điểm ban đầu.
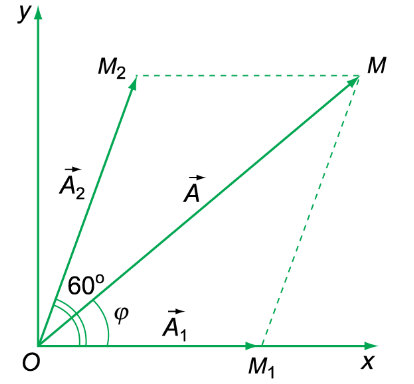 – Áp dụng các công thức tính biên độ và pha của dao động tổng hợp ta có:
– Áp dụng các công thức tính biên độ và pha của dao động tổng hợp ta có:
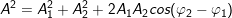
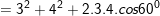
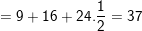
Vậy 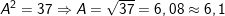
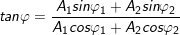
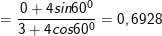
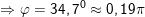
⇒ Vậy phương trình của dao động tổng hợp là: 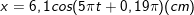
III. Bài tập về tổng hợp dao động cùng phương cùng tần số và lời giải
° Bài 1 trang 25 SGK Vật lý 12: Nêu cách biểu diễn một dao động điều hòa bằng một vecto quay.
* Lời giải bài 1 trang 25 SGK Vật lý 12:
– Mỗi dao động điều hòa x = Acos(ωt + φ) được biểu diễn bằng một vectơ quay. Vectơ quay có đặc điểm: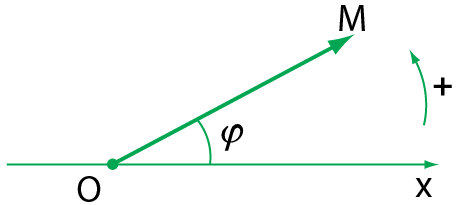 – Có gốc tại gốc tọa độ của trục Ox, có độ dài bằng biên độ dao động A và hợp với trục Ox một góc bằng pha ban đầu φ (chọn chiều dương là chiều của đường tròn lượng giác)
– Có gốc tại gốc tọa độ của trục Ox, có độ dài bằng biên độ dao động A và hợp với trục Ox một góc bằng pha ban đầu φ (chọn chiều dương là chiều của đường tròn lượng giác)
° Bài 2 trang 25 SGK Vật lý 12: Trình bày phương pháp giản đồ Fre-nen để tìm dao động tổng hợp của hai dao động điều hòa cùng phương, cùng tần số.
* Lời giải bài 2 trang 25 SGK Vật lý 12:
– Giả sử cần tổng hợp hai dao động điều hòa cùng phương, cùng tần số.
x1 = A1cos(ωt + φ1); x2 = A2cos(ωt + φ2)
– Lần lượt vẽ hai vectơ quay 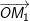 và
và 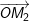 biểu diễn cho dao động x1 và dao động x2, lần lượt hợp với trục Ox những góc φ1, φ2.
biểu diễn cho dao động x1 và dao động x2, lần lượt hợp với trục Ox những góc φ1, φ2.
– Vẽ vectơ tổng hợp 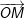 là tổng của hai vectơ
là tổng của hai vectơ 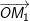 và
và 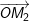 . Vectơ tổng hợp là vectơ quay biểu diễn phương trình của dao động tổng hợp.
. Vectơ tổng hợp là vectơ quay biểu diễn phương trình của dao động tổng hợp.
– Tìm độ dài của 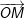 bằng công thức:
bằng công thức: 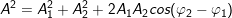
– Tìm góc hợp bởi 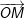 và trục Ox bằng công thức:
và trục Ox bằng công thức: 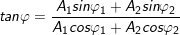
– Viết phương trình dao động tổng hợp dạng: x = A.cos(ωt + φ)
° Bài 3 trang 25 SGK Vật lý 12: Nêu ảnh hưởng của độ lệch pha (φ2 – φ1) đến biên độ của dao động tổng hợp trong các trường hợp:
a) Hai dao động thành phần cùng pha
b) Hai dao động thành phần ngược pha
c) Hai dao động thành phần có pha vuông góc 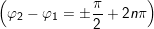
* Lời giải bài 3 trang 25 SGK Vật lý 12:
• Biên độ dao động tổng hợp phụ thuộc vào độ lệch pha Δφ = φ2 – φ1
– Nếu các dao động thành phần cùng pha, tức ∆φ = φ2 – φ1 = 2nπ, (n = 0, ±1, ±2,…), thì biên độ dao động tổng hợp là lớn nhất và bằng tổng hai biên độ: A = A1 + A2.
– Nếu hai dao động thành phần ngược pha, tức ∆φ = φ2 – φ1 = (2n+1)π, (n = 0, ±1, ±2,…), thì biên độ dao động tổng hợp là nhỏ nhất: A = |A1 – A2|.
– Nếu hai dao động thành phần có pha vuông góc Δφ = φ2 – φ1 = ±π/2 + 2nπ (n = 0, ±1, ±2,…) thì biên độ dao động tổng hợp 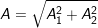
° Bài 4 trang 25 SGK Vật lý 12: Chọn đáp án đúng. Hai dao động là ngược pha khi:
A. φ2 – φ1 = 2nπ ;
B. φ2 – φ1 = nπ
C. φ2 – φ1 = (2n – 1)π ;
D. φ2 – φ1 = (2n + 1)π
* Lời giải bài 4 trang 25 SGK Vật lý 12:
– Đáp án đúng: D. φ2 – φ1 = (2n + 1)π
° Bài 5 trang 25 SGK Vật lý 12: Xét một vecto quay OM→ có những đặc điểm sau:
– Có độ lớn bằng hai đơn vị chiều dài.
– Quay quanh O với tốc độ góc 1 rad/s
– Tại thời điểm t = 0, vecto OM→ hợp với trục Ox một góc 30o
Hỏi vecto quay OM→ biểu diễn phương trình của dao động điều hòa nào?
A. x = 2cos(t – π/3) B. x = 2cos(t + π/6)
C. x = 2cos(t – 30o) D. x = 2cos(t + π/3)
* Lời giải bài 5 trang 25 SGK Vật lý 12:
– Đáp án đúng: B. x = 2cos(t + π/6)
• Vectơ quay OM→ có:
– Có độ lớn bằng hai đơn vị chiều dài nên biên độ dao động A = 2.
– Quay quanh O với tốc độ góc 1 rad/s nên tần số ω = 1 (rad/s).
– Tại thời điểm t = 0, vectơ 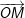 hợp với trục Ox một góc 30o nên pha ban đầu là φ = π/6 (rad).
hợp với trục Ox một góc 30o nên pha ban đầu là φ = π/6 (rad).
⇒ Phương trình dao động: x = 2.cos(t + π/6).
° Bài 6 trang 25 SGK Vật lý 12: Cho hai dao động điều hòa cùng phương, cùng tần số góc ω = 5π rad/s, với các biên độ: A1 = √3/2 cm, A2 = √3 cm và các pha ban đầu tương ứng φ1 = π/2 và π2 = 5π/6. Tìm phương trình dao động tổng hợp của hai dao động trên.
* Lời giải bài 6 trang 25 SGK Vật lý 12:
– Biểu diễn hai vecto A1 và A2 độ lớn lần lượt là 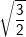 (cm),
(cm), 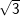 (cm) hợp với trục Ox lần lượt các góc 90o và 150o.
(cm) hợp với trục Ox lần lượt các góc 90o và 150o.
– Ta có công thức: A2 = A12 + A22 + 2A1A2 cos(φ2 – φ1) ⇒ A = 2,3 (cm).
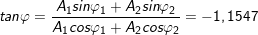
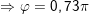
⇒ Vậy phương trình tổng hợp là: x = 2,3.cos(5πt + 0,73π) (cm)
Hy vọng với bài viết tổng hợp 2 giao động điều hòa cùng phương cùng tần số với phương pháp giản đồ FRE-NEN và bài tập ở trên giúp ích cho các em. Mọi góp ý và thắc mắc các em vui lòng để lại bình luận dưới bài viết để Trường Trung Cấp Nghề Thương Mại Du Lịch Thanh Hoá ghi nhận và hỗ trợ, chúc các em học tập tốt.
Bản quyền bài viết thuộc Trường Trung Cấp Nghề Thương Mại Du Lịch Thanh Hoá. Mọi hành vi sao chép đều là gian lận!
Nguồn chia sẻ: https://tmdl.edu.vn https://tmdl.edu.vn/vat-ly-12-bai-5/
Trang chủ: tmdl.edu.vn
Danh mục bài: Giáo dục




