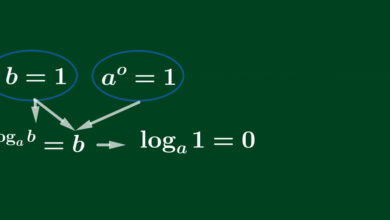Vectơ chỉ phương là gì? Cách tìm Vectơ chỉ phương của đường thẳng cực hay

Vectơ chỉ phương của đường thẳng là gì? Vectơ chỉ phương trong oxyz như nào? Cách tìm Vectơ chỉ phương của đường thẳng ra sao? … Đây là một trong những phần kiến thức Toán 10 vô cùng quan trong được nhiều học sinh quan tâm. Bài viết hôm nay, Trường Trung Cấp Nghề Thương Mại Du Lịch Thanh Hoá sẽ giải đáp tường tận cho các bạn nhé !

I. LÝ THUYẾT VỀ VECTƠ CHỈ PHƯƠNG CỦA ĐƯỜNG THẲNG

Bạn đang xem bài: Vectơ chỉ phương là gì? Cách tìm Vectơ chỉ phương của đường thẳng cực hay

1. Vecto chỉ phương của đường thẳng là gì?

– Giá của vectơ là đường thẳng đi qua điểm gốc và điểm ngọn của vectơ đó.

– Cho đường thẳng d. Ta có vecto được gọi là vectơ chỉ phương (VTCP) của đường thẳng d nếu giá của nó song song hoặc trùng với d.

– Nếu $overrightarrow{u}$ là VTCP của d thì cũng là VTCP của d.

– VTCP và VTPT vuông góc với nhau $Rightarrow overrightarrow{u}=left( a,b right)Rightarrow overrightarrow{n}=left( -b,a right)$ . Đây chính là cách chuyển từ VTCP sang VTPT và ngược lại.

– Ta có thể dễ dàng xác định được đường thẳng khi biết một điểm thuộc đường thẳng và VTCP của đường thẳng đó.

2. Hệ số góc của đường thẳng

– Phương trình đường thẳng d có dang: y = kx + b hay kx – y – b = 0

+ Hệ số góc của đường thẳng là k.

+ Vectơ pháp tuyến của đường thẳng là $overrightarrow{n}=left( k,-1 right)$

+ Vectơ chỉ phương của đường thẳng là: $overrightarrow{u}$

Ví dụ: Cho phương trình đường thẳng 3x + 2y = 1. Xác định vectơ chỉ phương, vectơ pháp tuyến, hệ số góc của đường thẳng.

Hướng dẫn:

+ Vectơ chỉ pháp tuyến của đường thẳng là $overrightarrow{n}=left( 3,2 right)$

+ Vectơ chỉ phương của đường thẳng là: $overrightarrow{u}$

+Ta viết lại phương trình đường thẳng $y=frac{-3}{2}x-frac{1}{2}$ . Hệ số góc của đường thẳng là $frac{3}{2}$ .

3. Phương trình tham số của đường thẳng

– Đường thẳng d đi qua A(m, n) nhận làm vectơ chỉ phương có phương trình tham số là:

$d:left{ begin{matrix} x=m+at y=n+bt end{matrix} right.$

Ví dụ 1 : Lập phương trình tham số đi qua điểm A(1, 2) và vectơ chỉ phương .

Hướng dẫn giải

Phương trình tham số của đường thẳng $d:left{ begin{matrix} x=1+t y=2+t end{matrix} right.$

Ví dụ 2: Vectơ chỉ phương của đường thẳng d: 2x – 5y – 100 = 0 là:

A. $vec{u}$ = (2; -5)

B. $vec{u}$ = (2; 5)

C. $vec{u}$ = (5; 2)

D. $vec{u}$ =( -5; 2)

Hướng dẫn giải

Đường thẳng d có VTPT là $vec{n}$ ( 2 ;- 5) .

⇒ Đường thẳng có VTCP là $vec{u}$ ( 5 ; 2).

4. Ứng dụng trong mặt phẳng tọa độ

Những bài toán ứng dụng tính chất của vectơ chỉ phương thường gặp nhất:

+ Xác định vectơ chỉ phương cho trước.

+ Viết phương trình đường thẳng đi qua một điểm và VTCP cho trước.

+ Xác định vị trí tương đối của 2 đường thẳng.

+ Tính khoảng cách từ một điểm đến một đường thẳng.

+ Biện luận, chứng minh phương trình đường thẳng.

Các tính chất của vecto chỉ phương sẽ xuất hiện xuyên suốt trong các bài tập tổng hợp về phương trình đường thẳng, học sinh cần nắm vững nội dung định nghĩa, tính chất của vectơ pháp tuyến.

II. CÁCH TÌM VECTƠ CHỈ PHƯƠNG CỦA ĐƯỜNG THẲNG CỰC HAY

1. Phương pháp giải

+ Cho đường thẳng d, một vecto u→ được gọi là VTCP của đường thẳng d nếu u→ có giá song song hoặc trùng với đường thẳng d.

+ Nếu vecto u→( a; b) là VTCP của đường thẳng d thì vecto k.u→ ( với k ≠ 0) cũng là VTCP của đường thẳng d.

+ Nếu đường thẳng d có VTPT n→( a; b) thì đường thẳng d nhận vecto n→( b; -a) và n’→( – b;a) làm VTPT.

2. Ví dụ minh họa

Ví dụ 1: Cho đường thẳng d đi qua A(- 2; 3) và điểm B(2; m + 1) . Tìm m để đường thẳng d nhận u→( 2; 4) làm VTCP?

A. m = – 2 B. m = -8 C. m = 5 D. m = 10

Lời giải

Đường thẳng d đi qua hai điểm A và B nên đường thẳng d nhận vecto AB→( 4; m – 2) làm VTCP.

Lại có vecto u→(2; 4) làm VTCP của đường thẳng d. Suy ra hai vecto u→ và ab→ cùng phương nên tồn tại số k sao cho: u→ = kAB→

Cách tìm vecto chỉ phương của đường thẳng cực hay - Toán lớp 10

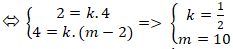
Vậy m = 10 là giá trị cần tìm .

Chọn D.

Ví dụ 2. Vectơ nào dưới đây là một vectơ chỉ phương của đường thẳng đi qua hai điểm A( a; 0) và B( 0; b)

A. u→( -a; b) B. u→( a; b) C. u→( a + b; 0) D. u→( – a; – b)

Lời giải

Đường thẳng AB đi qua điểm A và B nên đường thẳng này nhận AB→(-a;b) làm vecto chỉ phương.

Chọn A.

Ví dụ 3. Đường thẳng d có một vectơ pháp tuyến là u→ = (-2; -5) . Đường thẳng ∆ vuông góc với d có một vectơ chỉ phương là:

A. u₁→ = (5; -2) B. u₂→ = (-5; 2) C. u₃→ = (2; 5) D. u₄→ = (2; -5)

Lời giải

Khi hai đường thẳng vuông góc với nhau thì VTCP của đường thẳng này là VTPT của đường thẳng kia nên :

Cách tìm vecto chỉ phương của đường thẳng cực hay - Toán lớp 10

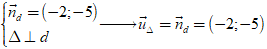
Lại có hai vecto u_∆→( -2; -5) và u→( 2;5) cùng phương nên đường thẳng ∆ nhận vecto u→( 2; 5) làm VTCP.

Chọn C.

Ví dụ 4. Đường thẳng d có một vectơ chỉ phương là u→ = (3; -4). Đường thẳng ∆ song song với d có một vectơ pháp tuyến là:

A. n₁→ = (4; 3) B. n₂→ = (- 4; 3) C. n₃→ = (3; 4) D. n₄→ = (3; – 4)

Lời giải

Khi hai đường thẳng song song với nhau thì VTCP ( VTPT) của đường thẳng này cũng là VTCP (VTPT) của đường thẳng kia nên:

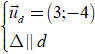Cách tìm vecto chỉ phương của đường thẳng cực hay - Toán lớp 10 → u_∆→ = u_d→ = (3; -4) → n_∆→ = (4; 3)

Chọn A

III. BÀI TẬP VẬN DỤNG

1. Bài tập có đáp án

Bài 1: Vectơ chỉ phương của đường thẳng d 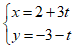Cách tìm vecto chỉ phương của đường thẳng cực hay - Toán lớp 10 là:

A. u₁→ = (2; -3) B. u₂→ = (3; -1) C. u₃→ = (3; 1) D. u₄→ = (3; -3)

Lời giải

Một VTCP của đường thẳng d là u→( 3; -1)

Chọn B

Bài 2: Vectơ nào dưới đây là một vectơ chỉ phương của đường thẳng đi qua hai điểm A(-3; 2) và B( 1; 4) ?

A. u₁→ = (-1; 2) B. u₂→ = (2; 1) C. u₃→ = (- 2; 6) D. u₄→ = (1; 1)

Lời giải

+ Đường thẳng AB đi qua hai điểm A và B nên đường thẳng này nhận vecto AB→( 4; 2) làm vecto chỉ phương .

+ Lại có vecto AB→ và u→( 2;1) là hai vecto cùng phương nên đường thẳng AB nhận vecto u→( 2;1) là VTCP.

Chọn B.

Bài 3: Vectơ chỉ phương của đường thẳng 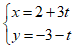Cách tìm vecto chỉ phương của đường thẳng cực hay - Toán lớp 10 = 1 là:

A. u₄→ = (-2; 3) B. u₂→ = (3; -2) C. u₃→ = (3; 2) D. u₁→ = (2; 3)

Hướng dẫn giải:

Ta đưa phương trình đường thẳng đã cho về dạng tổng quát:

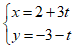Cách tìm vecto chỉ phương của đường thẳng cực hay - Toán lớp 10 = 1 ⇔ 2x + 3y – 6 = 0 nên đường thẳng có VTPT là n→ = (2; 3)

Suy ra VTCP là u→ = (3; – 2) .

Chọn B.

Bài 4: Vectơ chỉ phương của đường thẳng d: 2x – 5y – 100 = 0 là :

A. u→ = (2; -5) B. u→ = (2; 5) C. u→ = (5; 2) D. u→=( -5; 2)

Lời giải

Đường thẳng d có VTPT là n→( 2 ;- 5) .

⇒ đường thẳng có VTCP là u→( 5 ; 2).

Chọn C.

2. Bài luyện tập thêm:

Câu 1. Vectơ chỉ phương của đường thẳng d x = 2+3t và y = -3-t là:

A. $xrightarrow[u_1]{}$ = (2; -3)

B. $xrightarrow[u_2]{}$ = (3; -1)

C. $xrightarrow[u_3]{}$ = (3; 1)

D. $xrightarrow[u_4]{}$ = (3; -3)

Câu 2: Vectơ nào dưới đây là một vectơ chỉ phương của đường thẳng đi qua hai điểm A(-3; 2) và B (1; 4)?

A. $overrightarrow{u_1}$ = (-1; 2)

B. $overrightarrow{u_2}$ = (2; 1)

C. $overrightarrow{u_3}$ = (- 2; 6)

D. $overrightarrow{u_4}$ = (1; 1)

Câu 3: Vectơ chỉ phương của đường thẳng x = 2+3t và y = -3-t = 1 là:

A. $overrightarrow{u_4}$ = (-2; 3)

B. $overrightarrow{u_2}$ = (3; -2)

C. $overrightarrow{u_3}$ = (3; 2)

D. $overrightarrow{u_1}$ = (2; 3)

Câu 4: Vectơ chỉ phương của đường thẳng d: 2x – 5y – 100 = 0 là:

A. $overrightarrow u$ = (2; -5)

B. $overrightarrow u$ = (2; 5)

C. $overrightarrow u$ = (5; 2)

D. $overrightarrow u$ =( -5; 2)

Câu 5: Vectơ nào dưới đây là một vectơ pháp tuyến của đường thẳng đi qua hai điểm A(2 ; 3) và B( 4 ;1)

A. $overrightarrow n$ = (2; -2)

B. $overrightarrow n$ = (2; -1)

C. $overrightarrow n$ = (1; 1)

D. $overrightarrow n$ = (1; -2)

Câu 6: Vectơ nào dưới đây là một vectơ chỉ phương của đường thẳng song song với trục Ox

A. $overrightarrow{u_1}$ = (1; 0).

B. $overrightarrow{u_2}$ = (0; -1)

C. $overrightarrow{u_3}$ = (1; 1)

D. $overrightarrow{u_4}$ = (1; – 1)

Câu 7: Cho đường thẳng d đi qua A( 1; 2) và điểm B(2; m). Tìm m để đường thẳng d nhận $overrightarrow u$ (1; 3) làm VTCP?

A. m = – 2

B. m = -1

C. m = 5

D. m = 2

Câu 8: Cho đường thẳng d đi qua A(- 2; 3) và điểm B(2; m + 1) . Tìm m để đường thẳng d nhận $overrightarrow u$ ( 2; 4) làm VTCP?

A. m = – 2

B. m = -8

C. m = 5

D. m = 10

Câu 9: Vectơ nào dưới đây là một vectơ chỉ phương của đường thẳng đi qua hai điểm A( a; 0) và B( 0; b)

A. $overrightarrow u$ ( -a; b)

B. $overrightarrow u$ ( a; b)

C. $overrightarrow u$ ( a + b; 0)

D. $overrightarrow u$ ( – a; – b)

Trên đây Trường Trung Cấp Nghề Thương Mại Du Lịch Thanh Hoá đã giới thiệu đến các bạn lý thuyết về Vectơ chỉ phương và cách tìm Vectơ chỉ phương của đường thẳng cực hay. Hi vọng, đây sẽ là nguồn tư liệu thiết yếu giúp các bạn dạy và học tốt hơn. Xem thêm chuyên đề tích vô hướng của hai vectơ tại đường link này bạn nhé !

Bản quyền bài viết thuộc Trường Trung Cấp Nghề Thương Mại Du Lịch Thanh Hoá. Mọi hành vi sao chép đều là gian lận!
Nguồn chia sẻ: https://tmdl.edu.vn https://tmdl.edu.vn/vecto-chi-phuong-la-gi-cach-tim-vecto-chi-phuong-cua-duong-thang-cuc-hay/

Trang chủ: tmdl.edu.vn
Danh mục bài: Giáo dục

Lương Sinh15 Tháng Hai, 2023