Hướng dẫn cách tính đạo hàm của hàm số Logarit cực đơn giản
Lý thuyết về hàm số Logarit cùng cách tính đạo hàm của hàm số Logarit học sinh đã được tìm hiểu trong chương trình Toán 12. Đây là phần kiến thức vô cùng quan trọng có nhiều trong các loại đề thi. Bài viết hôm nay Trường Trung Cấp Nghề Thương Mại Du Lịch Thanh Hoá sẽ hệ thống lại tất cả các kiến thức cần ghi nhớ về chuyên đề này cùng nhiều mẹo hay để tính đạo hàm của hàm số Logarit cực dễ. Bạn tìm hiểu nhé !
I. LÝ THUYẾT VỀ HÀM SỐ LOGARIT
Bạn đang xem bài: Hướng dẫn cách tính đạo hàm của hàm số Logarit cực đơn giản
1. Hàm số Logarit là gì ?
Hàm số logarit là hàm số có dạng y = logax.
2. Tính chất của hàm số logarit y = logax (a>0,a≠1)(a>0,a≠1).
– Tập xác định: (0;+∞)(0;+∞).
– Đạo hàm ∀x∈(0;+∞),y′=1xlna∀x∈(0;+∞),y′=1xlna.
– Chiều biến thiên:
+) Nếu a>1a>1 thì hàm số luôn đồng biến
+) Nếu 0<a<10<a<1 thì hàm số luôn nghịch biến
– Tiệm cận: Trục Oy là tiệm cận đứng.
– Đồ thị nằm hoàn toàn phía bên phải trục tung, luôn cắt trục hoành tại điểm (1;0)(1;0) và đi qua điểm (a;1)(a;1).
3. Chú ý
– Nếu a>1a>1 thì lna>0lna>0, suy ra (ax)′>0∀x(ax)′>0∀x và (logax)’ > 0, ∀x > 0;
do đó hàm số mũ và hàm số lôgarit với cơ số lớn hơn 1 đều là những hàm số luôn luôn đồng biến.
Tương tự, nếu 0<a<10<a<1 thì lna<0lna<0, (ax)’ < 0 và (logax)’ < 0, ∀x > 0; hàm số mũ và hàm số lôgarit với cơ số nhỏ hơn 1 đều là những hàm số luôn luôn nghịch biến.
– Công thức đạo hàm của hàm số lôgarit có thể mở rộng thành
(ln|x|)′=1/x,∀x≠0 và (loga|x|)’ = 1/xlna, ∀x≠≠ 0.
II. CÔNG THỨC TÍNH ĐẠO HÀM CỦA HÀM SỐ LOGARIT
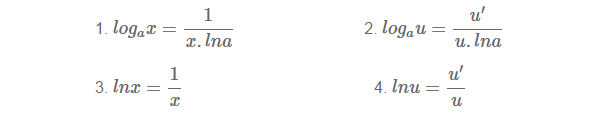
Ví dụ:
Tính đạo hàm của hàm số 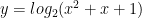 .
.
Lời giải:
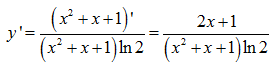 Trường hợp đặc biệt, khi cơ số của hàm logarit là e. Hay y=lnx. Ta có công thức đạo hàm như sau:
Trường hợp đặc biệt, khi cơ số của hàm logarit là e. Hay y=lnx. Ta có công thức đạo hàm như sau:
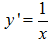 Nếu y=lnu(x) thì ta có:
Nếu y=lnu(x) thì ta có:
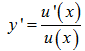
III. BÀI TẬP VỀ ĐẠO HÀM CỦA HÀM SỐ LOGARIT

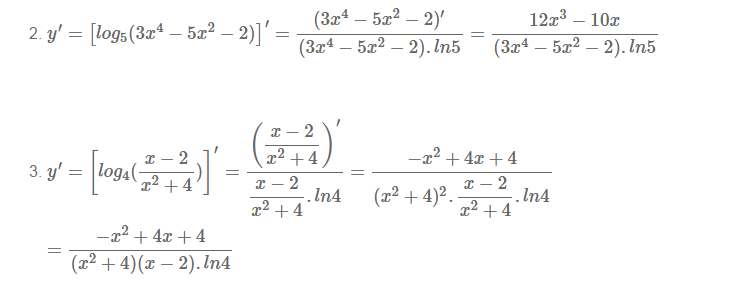
Với hướng dẫn trên các em làm tiếp các bài tập dưới đây:

| Bài 3. Nghiệm của phương trình |
|
| A. |
B. |
| C. |
D. |
Lời giải chi tiết
Bài 4. Tập nghiệm S của phương trình 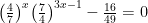 là là |
|
A. 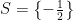 . . |
B. 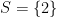 . . |
C. 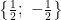 . . |
D. 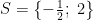 . . |
Lời giải chi tiết
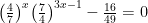
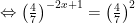
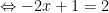
.
Bài 5. Nghiệm của phương trình 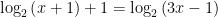 là là |
|
A. 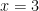 . . |
B. 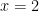 . . |
C. 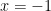 . . |
D. 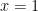 . . |
Lời giải chi tiết
Điều kiện
.
Vậy phương trình có nghiệm
.
Bài 6. Số nghiệm thực của phương trình 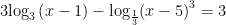 là là |
|
A. 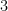 |
B. 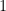 |
C. 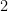 |
D. 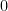 |
Lời giải chi tiết
Điều kiện:
.
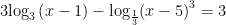
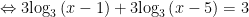
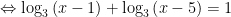
![Leftrightarrow {{log }_{3}}left[ left( x-1 right)left( x-5 right) right]=1 Leftrightarrow {{log }_{3}}left[ left( x-1 right)left( x-5 right) right]=1](https://tmdl.edu.vn/wp-content/uploads/2023/03/latex-95.png)
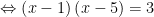
Đối chiếu điều kiện suy ra phương trình có 1 nghiệm
Bài 7. Số nghiệm của phương trình ![left( x-2 right)left[ {{log }_{0,5}}left( {{x}^{2}}-5x+6 right)+1 right]=0 left( x-2 right)left[ {{log }_{0,5}}left( {{x}^{2}}-5x+6 right)+1 right]=0](https://tmdl.edu.vn/wp-content/uploads/2023/03/latex-99.png) là là |
|
| A. 1. | B. 0. |
| C. 3. | D. 2. |
Lời giải chi tiết
ĐKXĐ:
.
Đối chiếu với ĐKXĐ ta thấy phương trình đã cho có 2 nghiệm.
Bài 8. Tổng tất cà các nghiệm của phương trình 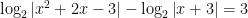 là là |
|
A. 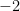 . . |
B. 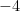 . . |
C. 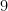 . . |
D. 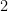 . . |
Lời giải chi tiết
Điều kiện:
Ta có:
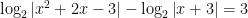
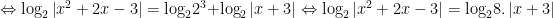

Vậy tổng các nghiệm của phương trình là
Bài 9. Số nghiệm của phương trình 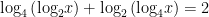 là là |
|
A. 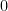 . . |
B. 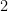 . . |
C. 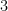 . . |
D. 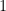 . . |
Lời giải chi tiết
Điều kiện:
.
Ta có: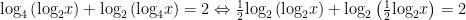
thỏa mãn điều kiện.
Vậy là các bạn vừa được tìm hiểu cách tính đạo hàm của hàm số Logarit cự đơn giản cùng nhiều bài tập vận dụng. Hi vọng, chia sẻ cùng bài viết bạn có thêm nguồn tư liệu quý phục vụ quá trình dạy và học được tốt hơn. Xem đầy đủ bảng công thức đạo hàm tại đường linh này nhé !
tmdl.edu.vn. Mọi hành vi sao chép đều là gian lận!
Nguồn chia sẻ: https://tmdl.edu.vn/huong-dan-cach-tinh-dao-ham-cua-ham-so-logarit-cuc-don-gian/
Trang chủ: tmdl.edu.vn
Danh mục bài: Giáo dục
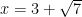
![left( x-2 right)left[ {{log }_{0,5}}left( {{x}^{2}}-5x+6 right)+1 right]=0Leftrightarrow {{log }_{0,5}}left( {{x}^{2}}-5x+6 right)=-1 left( x-2 right)left[ {{log }_{0,5}}left( {{x}^{2}}-5x+6 right)+1 right]=0Leftrightarrow {{log }_{0,5}}left( {{x}^{2}}-5x+6 right)=-1](https://tmdl.edu.vn/wp-content/uploads/2023/03/latex-100.png)